Bài 62 sách giải tích 12 nâng cao trang 118

Vẽ đồ thị của hàm số . Dựa vào đồ thị, hãy giải thích các bất phương trình sau:

Lựa chọn câu để xem lời giải nhanh hơn

Vẽ đồ thị của hàm số \(y = {\left( {\sqrt 3 } \right)^x}\). Dựa vào đồ thị, hãy giải các bất phương trình sau:

a) \({\left( {\sqrt 3 } \right)^x} \le 1\);

b) \({\left( {\sqrt 3 } \right)^x} > 3\).

LG a

\({\left( {\sqrt 3 } \right)^x} \le 1\);

Lời giải chi tiết:

* Vẽ đồ thị của hàm số \(y = {\left( {\sqrt 3 } \right)^x}\)

TXĐ: \(D =\mathbb R\)

Hàm số đồng biến trên R.

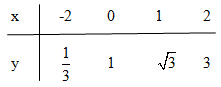
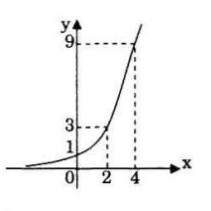
* Giải bất phương trình \({\left( {\sqrt 3 } \right)^x} \le 1\)

\({\left( {\sqrt 3 } \right)^x} \le 1 \Leftrightarrow x \le 0\) (ứng với những điểm trên đồ thị có tung độ nhỏ hơn hoặc bằng 1)

LG b

\({\left( {\sqrt 3 } \right)^x} > 3\)

Lời giải chi tiết:

TXĐ: \(D =\mathbb R\)

Hàm số đồng biến trên R.

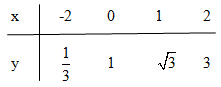
\({\left( {\sqrt 3 } \right)^x} > 3 \Leftrightarrow x > 2\) (ứng với những điểm trên đồ thị có tung độ lớn hơn 3).

Loigiaihay.com

👉

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 5 phiếu

Bài 61 sách giải tích 12 nâng cao trang 118
Vẽ đồ thị hàm số
Bài 60 sách giải tích 12 nâng cao trang 117
a) Chứng minh rằng đồ thị của hai hàm số đối xứng với nhau qua trục tung. b) Chứng minh rằng đồ thị của hai hàm số đối xứng với nhau qua trục hoành.
Bài 59 sách giải tích 12 nâng cao trang 117
Tính giá trị gần đúng đạo hàm của mỗi hàm số sau tại điểm đã cho (chính xác đến hàng phần trăm):
Bài 58 sách giải tích 12 nâng cao trang 117
Tìm đạo hàm của các hàm số sau:
Bài 57 sách giải tích 12 nâng cao trang 117
Trên hình bên cho hai đường cong (C1) (đường nét liền) và (C2) (đường nét đứt) được vẽ trên cùng một mặt phẳng tọa độ. Biết rằng mỗi đường cong ấy là đồ thị của ột trong hai hàm số lũy thừa và . Chỉ dựa vào tính chất của lũy thừa, có thể nhận biết đường cong nào là đồ thị của hàm số nào được không? Hãy nêu rõ lập luận.