-
GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
- Bài 1. Tính đơn điệu của hàm số
- Bài 2. Cực trị của hàm số
- Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Bài 4. Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5. Đường tiệm cận của đồ thị hàm số
- Bài 6. Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị hàm số của một số hàm phân thức hữu tỉ
- Bài 8. Một số bài toán thường gặp về đồ thị
- Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Bài tập trắc nghiệm khách quan chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số - Toán 12 Nâng cao
-
CHƯƠNG II. HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3. Lôgarit
- Bài 4. Số e và loogarit tự nhiên
- Bài 5. Hàm số mũ và hàm số lôgarit
- Bài 6. Hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Hệ phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Bài tập trắc nghiệm khách quan chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit - Toán 12 Nâng cao
-
CHƯƠNG III. NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
- Bài 1. Nguyên hàm
- Bài 2. Một số phương pháp tìm nguyên hàm
- Bài 3. Tích phân
- Bài 4. Một số phương pháp tích phân
- Bài 5. Ứng dụng tích phân để tính diện tích hình phẳng
- Bài 6. Ứng dụng tích phân để tính thể tích vật thể
- Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
- Bài tập trắc nghiệm khách quan chương III - Nguyên hàm, tích phân và ứng dụng - Toán 12 Nâng cao
-
CHƯƠNG IV. SỐ PHỨC
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
-
HÌNH HỌC - TOÁN 12 NÂNG CAO
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
Bài 59 Trang 177 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng A được giới hạn bởi đường cong có phương trình và các đường thẳng Tính thể tích khối tròn xoay tạo được khi quay A
Cho hình phẳng A được giới hạn bởi đường cong có phương trình \({y^2} = {x^3}\) và các đường thẳng \(y = 0,x = 1.\) Tính thể tích khối tròn xoay tạo được khi quay A
LG a
Quanh trục hoành;
Phương pháp giải:
Sử dụng công thức tính thể tích \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
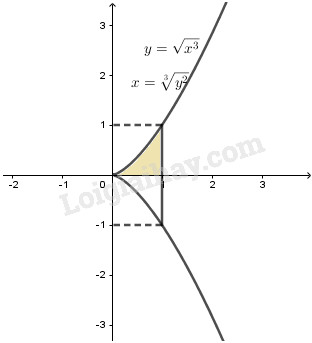
Ta có \({y^2} = {x^3} \Leftrightarrow y = \pm \sqrt {{x^3}} \)
\( \Rightarrow y = \sqrt {{x^3}} \,\,\left( {y \ge 0} \right)\)
Thể tích cần tìm là: \(V = \pi \int\limits_0^1 {{{\left( {\sqrt {{x^3}} } \right)}^2}dx} \) \( = \pi \int\limits_0^1 {{x^3}dx = \left. {{{\pi {x^4}} \over 4}} \right|} _0^1 = {\pi \over 4}\)
LG b
Quanh trục tung.
Phương pháp giải:
Sử dụng công thức tính thể tích \(V = \pi \int\limits_a^b {|{f^2}\left( y \right)-g^2(y)|dy} \)
Lời giải chi tiết:
Ta có \(x = \root 3 \of {{y^2}} \)
Thể tích cần tìm là: \(V = \pi \int\limits_0^1 {\left( {{1^2}-\root 3 \of {{y^4}} } \right)} dy \) \( = \pi \int\limits_0^1 {\left( {1 - {y^{\frac{4}{3}}}} \right)dy} \) \(= \left. {\pi \left( {y - {3 \over 7}{y^{{7 \over 3}}}} \right)} \right|_0^1 = {{4\pi } \over 7}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 58 Trang 177 SGK Đại số và Giải tích 12 Nâng cao
- Bài 57 Trang 177 SGK Đại số và Giải tích 12 Nâng cao
- Bài 56 Trang 177 SGK Đại số và Giải tích 12 Nâng cao
- Bài 55 Trang 177 SGK Đại số và Giải tích 12 Nâng cao
- Bài 54 Trang 177 SGK Đại số và Giải tích 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
