Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Ninh Bình
I. Phần trắc nghiệm
Đề bài
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội q = 3. Số hạng \({u_3}\)của cấp số nhân đã cho là
-
A.
18
-
B.
5
-
C.
6
-
D.
8
-
A.
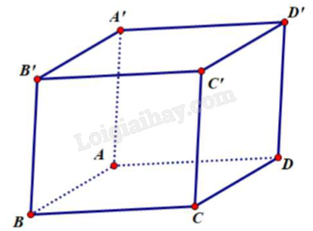
\(\overrightarrow {AB'} + \overrightarrow {CB} = \overrightarrow {AC'} \)
-
B.
\(\overrightarrow {AC} + \overrightarrow {BB'} = \overrightarrow {AC'} \)
-
C.
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
-
D.
\(\overrightarrow {AD} + \overrightarrow {CC'} = \overrightarrow {AD'} \)
Tập nghiệm của bất phương trình \({(0,21)^x} < 1\) là
-
A.
\(( - \infty ;0]\)
-
B.
\([0; + \infty )\)
-
C.
\(( - \infty ;0)\)
-
D.
\((0; + \infty )\)
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (với \(a \ne 0\), \(m \ne 0\)) có đồ thị như hình vẽ dưới đây.
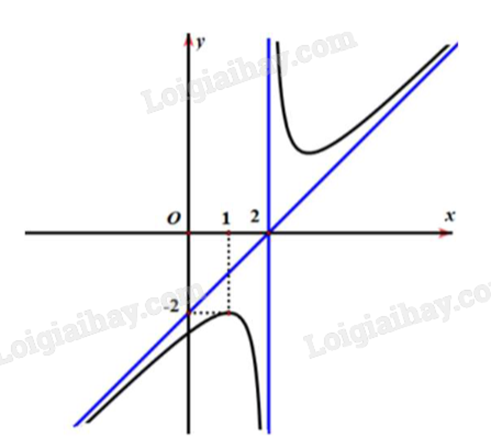
Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là
-
A.
y = 2x + 2
-
B.
y = x – 2
-
C.
y = 2x – 2
-
D.
y = x + 2
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình vẽ dưới đây.
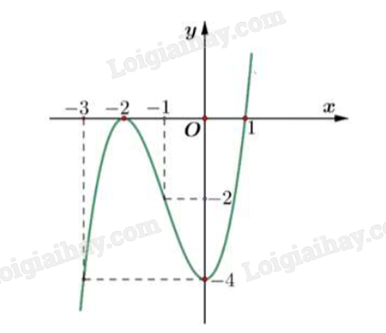
Hàm số y = f(x) đồng biến trên khoảng
-
A.
\(( - \infty ;0)\)
-
B.
\(( - 2;0)\)
-
C.
\(( - 4; + \infty )\)
-
D.
\((0; + \infty )\)
Nghiệm của phương trình \({\log _2}(x - 1) = 3\) là
-
A.
9
-
B.
8
-
C.
10
-
D.
7
Trong không gian Oxy, cho điểm A(-5;2;3) và B là điểm đối xứng với A qua trục Oy. Độ dài đoạn thẳng AB bằng
-
A.
\(\sqrt {34} \)
-
B.
\(\sqrt 8 \)
-
C.
\(2\sqrt {34} \)
-
D.
\(\sqrt {38} \)
Lớp 12A8 của trường THPT X có 41 học sinh được đánh số thứ tự từ 1 đến 41. Cô giáo chọn ngẫu
nhiên 3 bạn để làm nhiệm vụ kiểm tra vở bài tập của các bạn trong lớp. Xác suất để 3 bạn được chọn có số thứ tự lập thành một cấp số cộng là \(\frac{a}{b}\) (với \(\frac{a}{b}\) là phân số tối giản). Tính S = 2a + b.
-
A.
553
-
B.
573
-
C.
653
-
D.
613
Cho hình hộp ABC.A’B’C’D’. Mệnh đề nào dưới đây là sai?
-
A.
(ADD’A’) // (BCC’B’)
-
B.
(BDA’) // (B’D’C)
-
C.
(ABA’) // (B’D’C)
-
D.
(ABCD) // (A’B’C’D’)
Để chuẩn bị cho tiết học “Mạng xã hội: lợi và hại” (Hoạt động thực hành trải nghiệm môn Toán,
lớp 10), giáo viên đã khảo sát thời gian sử dụng mạng xã hội trong một ngày của học sinh trong lớp 10A1
mình dạy và thu được mẫu số liệu như sau:
Thời gian trung bình (phút) sử dụng mạng xã hội của học sinh lớp 10A1 xấp xỉ bằng
-
A.
35
-
B.
30,5
-
C.
36,3
-
D.
33,6
Phương trình tanx = -1 có tất cả các nghiệm là
-
A.
\(\frac{\pi }{4} + k2\pi \) \((k \in \mathbb{Z})\).
-
B.
\( - \frac{\pi }{4} + k2\pi \) \((k \in \mathbb{Z})\).
-
C.
\(\frac{\pi }{4} + k\pi \) \((k \in \mathbb{Z})\).
-
D.
\( - \frac{\pi }{4} + k\pi \) \((k \in \mathbb{Z})\).
-
A.
2
-
B.
1
-
C.
-1
-
D.
-2
Cho hàm số \(y = f(x) = \frac{{a{x^2} + bx + c}}{{x + d}}\) có đồ thị là đường cong trong hình vẽ dưới đây, biết đường tiệm cận xiên của đồ thị hàm số đi qua hai điểm (0;1) và (1;0).
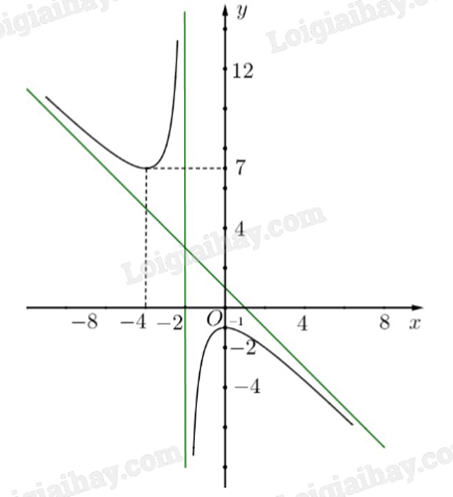
a) Hàm số đồng biến trên khoảng (-4;0).
b) Ta có a + b + c + d = -2.
c) Khoảng cách từ M(1;-8) đến đường thẳng đi qua các điểm cực trị của đồ thị hàm số là \(\sqrt 5 \).
d) Tập xác định của hàm số là \(\mathbb{R}\backslash \{ 2\} \).
Cho hàm số \(y = f(x) = {e^{x + \sqrt {16 - {x^2}} }}\).
a) f’(x) = 0 có hai nghiệm phân biệt.
b) \(f'(x) = \left( {1 - \frac{x}{{\sqrt {16 - {x^2}} }}} \right){e^{x + \sqrt {16 - {x^2}} }}\), \(\forall x \in [ - 4;4]\).
c) Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) là \({e^{a + b\sqrt c }}\) (với \(a,b,c \in \mathbb{Z}\) và c là số nguyên tố). Khi đó a + 2b + 3c = 10.
d) \(f( - 4) = \frac{1}{{{e^4}}}\).
Một hạt chuyển động trên một đường thẳng có gắn một trục tọa độ với gốc tọa độ là vị trí hạt bắt đầu chuyển động. Tọa độ của hạt trên trục tại thời điểm t (đơn vị: giây) kể từ khi xuất phát được cho bởi công thức x(t) = 2t – 3ln(t + 1) (đơn vị: mét), \(t \ge 0\). Hàm số v(t) = x’(t) (đơn vị: mét/giây) biểu thị vận tốc chuyển động của hạt.
a) Quãng đường mà hạt đi được trong 3 giây đầu tiên là 1,84 m (làm tròn kết quả đến hàng phần trăm).
b) Hạt đứng yên tại thời điểm t = 0,5 s.
c) \(v(t) = 2 - \frac{3}{{t + 1}}\).
d) Vận tốc ban đầu của hạt là 1 m/s.
Một kho chứa hàng có dạng hình lăng trụ đứng ABFPE.DCGQH với ABFE là hình chữ nhật và
EFP là tam giác cân tại P. Gọi T là trung điểm của DC. Các kích thước của kho chứa lần lượt là
AB = 6 m; AE = 5 m; AD = 8 m; QT = 7 m. Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có
gốc toạ độ là điểm O thuộc đoạn AD sao cho OA = 2 m và các trục toạ độ tương ứng như hình vẽ dưới đây.
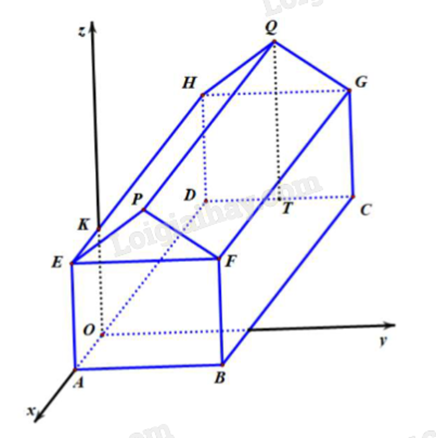
a) Tọa độ điểm Q là (-6;3;5).
b) Vecto \(\overrightarrow {OC} \) có tọa độ là (-6;6;0).
c) Người ta muốn lắp camera quan sát trong nhà kho tại vị trí trung điểm của FG và đầu thu dữ liệu đặt tại vị trí O. Người ta thiết kế đường dây cáp nối từ O đến K sau đó nối thẳng đến camera. Độ dài đoạn cáp nối tối thiểu bằng \(5 + 2\sqrt {10} \) m.
d) Mái nhà được lợp bằng tôn Hoa Sen, giá tiền mỗi mét vuông tôn là 130000 đồng. Số tiền cần bỏ ra để mua tôn lợp mái nhà là 3750000 đồng (không kể hao phí do việc cắt và ghép các miếng tôn, làm tròn kết quả đến hàng nghìn).
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thoi tâm O, SO vuông góc với mặt đáy. Biết cạnh hình thoi bằng 2024, góc BAD bằng \({120^o}\), khoảng cách từ điểm C đến mặt phẳng (SBD) bằng bao nhiêu?
Đáp án:
Trong không gian Oxyz, một khinh khí cầu ở tọa độ A(-16;-10;10) bắt đầu bay với vecto vận tốc
không đổi \(\overrightarrow v = (4;3; - 1)\) (đơn vị vận tốc là km/h) và dự kiến bay trong thời gian 10 giờ. Biết trạm kiểm soát không lưu đặt ở vị trí gốc toạ độ O kiểm soát được các vật thể cách trạm một khoảng tối đa bằng 12 km. Thời gian kể từ khi trạm kiểm soát không lưu phát hiện ra khinh khí cầu đến khi khinh khí cầu ra khỏi vùng kiểm soát là bao nhiêu phút?
Đáp án:
Một thanh dầm hình hộp chữ nhật được cắt từ một khúc gỗ hình trụ có bán kính đáy bằng 20 cm sao cho thanh dầm có diện tích mặt cắt ngang lớn nhất, tức là thanh dầm có mặt cắt ngang là hình vuông. Sau khi cắt thanh dầm đó, người ta lại cắt bốn tấm ván hình hộp chữ nhật từ bốn phần còn lại của khúc gỗ (tham khảo hình vẽ dưới đây). Xác định diện tích mặt cắt ngang tối đa của mỗi tấm ván (theo đơn vị \(c{m^2}\) và làm tròn kết quả đến hàng phần chục).
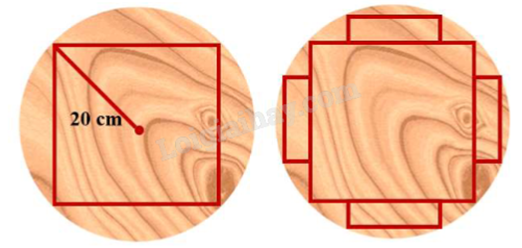
Đáp án:
Trong một chiếc hộp có 30 viên bi có cùng kích thước và khối lượng, trong đó có 6 viên bi màu đỏ, 7 viên bi màu xanh, 8 viên bi màu vàng và 9 viên bi màu trắng. Lấy ngẫu nhiên đồng thời 3 viên bi. Xác suất để 3 viên bi lấy ra có đúng hai màu bằng \(\frac{a}{b}\), với \(\frac{a}{b}\) là phân số tối giản. Tổng a + b bằng bao nhiêu?
Đáp án:
Một nhà máy sản xuất x sản phẩm trong mỗi tháng. Chi phí sản xuất x sản phẩm được cho bởi hàm chi phí \(C(x) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}\) (nghìn đồng). Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm x và được cho bởi công thức \(p(x) = 1700 - 7x\) (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.
Đáp án:
Một kỹ sư thiết kế mô hình trang trí cho một sân khấu nổi có dạng hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\) với độ dài các cạnh bằng 5 m. Để tạo ra nét độc đáo cho sân khấu, người kỹ sư muốn thiết kế một dàn đèn ánh sáng nối từ một điểm M trên đường chéo \(A{D_1}\) xuống một điểm N trên mặt đất BD đồng thời AM = DB. Dàn đèn ánh sáng có chiều dài ngắn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm).
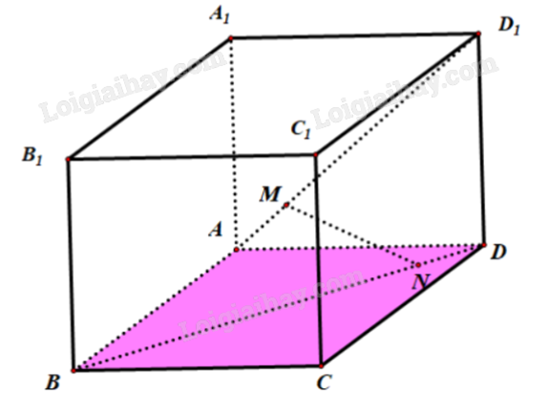
Đáp án:
Lời giải và đáp án
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội q = 3. Số hạng \({u_3}\)của cấp số nhân đã cho là
-
A.
18
-
B.
5
-
C.
6
-
D.
8
Đáp án : A
Áp dụng công thức số hạng tổng quát của cấp số nhân: \({u_n} = {u_1}{q^{n - 1}}\).
\({u_3} = {u_1}{q^2} = {2.3^2} = 18\).
-
A.
\(\overrightarrow {AB'} + \overrightarrow {CB} = \overrightarrow {AC'} \)
-
B.
\(\overrightarrow {AC} + \overrightarrow {BB'} = \overrightarrow {AC'} \)
-
C.
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
-
D.
\(\overrightarrow {AD} + \overrightarrow {CC'} = \overrightarrow {AD'} \)
Đáp án : A
Áp dụng quy tắc cộng, trừ vecto, khái niệm hai vecto bằng nhau, quy tắc hình bình hành để chứng minh các đẳng thức trên đúng hoặc sai.
- Xét đáp án A:
Giả sử đẳng thức đúng: \(\overrightarrow {AB'} + \overrightarrow {CB} = \overrightarrow {AC'} \Leftrightarrow \overrightarrow {AB'} - \overrightarrow {AC'} = - \overrightarrow {CB} \Leftrightarrow \overrightarrow {AB'} + \overrightarrow {C'A} = \overrightarrow {BC} \Leftrightarrow \overrightarrow {C'B'} = \overrightarrow {BC} \) (vô lí vì hai vecto này ngược hướng).
Vậy đẳng thức A sai.
- Xét đáp án B:
\(\overrightarrow {AC} + \overrightarrow {BB'} = \overrightarrow {AC} + \overrightarrow {CC'} = \overrightarrow {AC'} \).
Vậy đẳng thức B đúng.
- Xét đáp án C:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) đúng theo quy tắc hình bình hành.
Vậy đẳng thức C đúng.
- Xét đáp án D:
\(\overrightarrow {AD} + \overrightarrow {CC'} = \overrightarrow {AD} + \overrightarrow {DD'} = \overrightarrow {AD'} \).
Vậy đẳng thức D đúng.
Tập nghiệm của bất phương trình \({(0,21)^x} < 1\) là
-
A.
\(( - \infty ;0]\)
-
B.
\([0; + \infty )\)
-
C.
\(( - \infty ;0)\)
-
D.
\((0; + \infty )\)
Đáp án : D
Với 0 < a < 1 thì tập nghiệm của bất phương trình \({a^x} < b\) là \(({\log _a}b; + \infty )\).
TXĐ: \(D = \mathbb{R}\).
\({(0,21)^x} < 1 \Leftrightarrow x > {\log _{0,21}}1 \Leftrightarrow x > 0\).
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (với \(a \ne 0\), \(m \ne 0\)) có đồ thị như hình vẽ dưới đây.
Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là
-
A.
y = 2x + 2
-
B.
y = x – 2
-
C.
y = 2x – 2
-
D.
y = x + 2
Đáp án : B
Dựa vào tọa độ các điểm mà đường tiệm cận đi qua, giải hệ phương trình tìm ra các hệ số.
Phương trình đường tiệm cận xiên có dạng y = ax + b \((a \ne 0)\).
Đường tiệm cận xiên đi qua hai điểm có tọa độ (2;0) và (0;-2) nên ta có:
\(\left\{ \begin{array}{l}0 = a.2 + b\\ - 2 = a.0 + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\end{array} \right.\).
Vậy phương trình đường tiệm cận xiên là y = x – 2.
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình vẽ dưới đây.
Hàm số y = f(x) đồng biến trên khoảng
-
A.
\(( - \infty ;0)\)
-
B.
\(( - 2;0)\)
-
C.
\(( - 4; + \infty )\)
-
D.
\((0; + \infty )\)
Đáp án : D
Hàm số đồng biến trên khoảng đồ thị đi lên từ trái sang.
Hàm số đồng biến trên khoảng \((0; + \infty )\).
Nghiệm của phương trình \({\log _2}(x - 1) = 3\) là
-
A.
9
-
B.
8
-
C.
10
-
D.
7
Đáp án : A
\({\log _a}x = b \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x = {a^b}\end{array} \right.\).
\({\log _2}(x - 1) = 3 \Leftrightarrow \left\{ \begin{array}{l}x - 1 > 0\\x - 1 = {2^3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x = 9\end{array} \right. \Leftrightarrow x = 9\).
Trong không gian Oxy, cho điểm A(-5;2;3) và B là điểm đối xứng với A qua trục Oy. Độ dài đoạn thẳng AB bằng
-
A.
\(\sqrt {34} \)
-
B.
\(\sqrt 8 \)
-
C.
\(2\sqrt {34} \)
-
D.
\(\sqrt {38} \)
Đáp án : C
Điểm A’ đối xứng với A(a;b;c) qua trục Oy có tọa độ (-a;b;-c).
Áp dụng công thức tính khoảng cách giữa hai điểm A, B: \(AB = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2} + {{({z_B} - {z_A})}^2}} \).
B đối xứng với A qua Oy nên B(5;2;-3).
\(AB = \sqrt {{{(5 + 5)}^2} + {{(2 - 2)}^2} + {{( - 3 - 3)}^2}} = 2\sqrt {34} \).
Lớp 12A8 của trường THPT X có 41 học sinh được đánh số thứ tự từ 1 đến 41. Cô giáo chọn ngẫu
nhiên 3 bạn để làm nhiệm vụ kiểm tra vở bài tập của các bạn trong lớp. Xác suất để 3 bạn được chọn có số thứ tự lập thành một cấp số cộng là \(\frac{a}{b}\) (với \(\frac{a}{b}\) là phân số tối giản). Tính S = 2a + b.
-
A.
553
-
B.
573
-
C.
653
-
D.
613
Đáp án : B
Áp dụng tính chất của cấp số cộng: \({u_n} = \frac{{{u_{n - 1}} + {u_{n + 1}}}}{2}\).
Xét phép thử T: “Chọn ngẫu nhiên 3 học sinh trong 41 học sinh của lớp 12A8”.
Ta có \(n(\Omega ) = C_{41}^3\).
Gọi A là biến cố: “3 học sinh được chọn có số thứ tự lập thành một cấp số cộng”.
Gọi a, b, c là ba số hạng liên tiếp của cấp số cộng. Vì \(b = \frac{{a + c}}{2}\) nên a và c có cùng tính chẵn, lẻ.
Từ 1 đến 41 có 20 số chẵn và 21 số lẻ nên ta có \(n(A) = C_{20}^2 + C_{21}^2\).
Do đó, xác suất của biến cố A là \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{20}}{{533}}\).
Vậy S = 2a + b = 2.20 + 533 = 573.
Cho hình hộp ABC.A’B’C’D’. Mệnh đề nào dưới đây là sai?
-
A.
(ADD’A’) // (BCC’B’)
-
B.
(BDA’) // (B’D’C)
-
C.
(ABA’) // (B’D’C)
-
D.
(ABCD) // (A’B’C’D’)
Đáp án : C
Hai mặt phẳng song song với nhau nếu một mặt phẳng chứa hai đường thẳng cắt nhau song song với mặt phẳng còn lại.
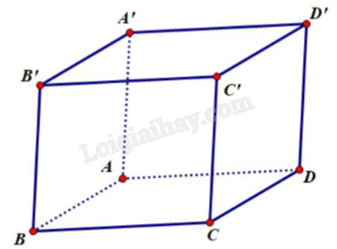
Dễ thấy các mệnh đề ở đáp án A, D đúng (hai mặt phẳng đối diện của hình hộp song song với nhau).
Xét đáp án B: \(\left\{ \begin{array}{l}BD//B'D' \Rightarrow BD//(B'D'C)\\A'B//D'C \Rightarrow A'B//(B'D'C)\\A'B \cap BD = \{ B\} \end{array} \right. \Rightarrow (BDA')//(B'D'C)\).
Vậy mệnh đề đáp án B đúng.
Xét đáp án C: (ABA’) chính là (ABB’A’). Mà (ABB’A’) giao (B’D’C) tại B’ nên hai mặt phẳng này không song song với nhau.
Vậy mệnh đề đáp án C sai.
Để chuẩn bị cho tiết học “Mạng xã hội: lợi và hại” (Hoạt động thực hành trải nghiệm môn Toán,
lớp 10), giáo viên đã khảo sát thời gian sử dụng mạng xã hội trong một ngày của học sinh trong lớp 10A1
mình dạy và thu được mẫu số liệu như sau:
Thời gian trung bình (phút) sử dụng mạng xã hội của học sinh lớp 10A1 xấp xỉ bằng
-
A.
35
-
B.
30,5
-
C.
36,3
-
D.
33,6
Đáp án : C
Tìm giá trị đại diện của từng nhóm rồi sử dụng công thức tính số trung bình của mẫu số liệu ghép nhóm.
Thời gian trung bình (phút) sử dụng mạng xã hội của học sinh lớp 10A1 xấp xỉ bằng:
\(\overline x = \frac{{15.5 + 25.10 + 35.15 + 45.7 + 55.5 + 65.3}}{{5 + 10 + 15 + 7 + 5 + 3}} \approx 36,3\).
Phương trình tanx = -1 có tất cả các nghiệm là
-
A.
\(\frac{\pi }{4} + k2\pi \) \((k \in \mathbb{Z})\).
-
B.
\( - \frac{\pi }{4} + k2\pi \) \((k \in \mathbb{Z})\).
-
C.
\(\frac{\pi }{4} + k\pi \) \((k \in \mathbb{Z})\).
-
D.
\( - \frac{\pi }{4} + k\pi \) \((k \in \mathbb{Z})\).
Đáp án : D
\(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \) \((k \in \mathbb{Z})\).
\(\tan x = - 1 \Leftrightarrow x = - \frac{\pi }{4} + k\pi \) \((k \in \mathbb{Z})\).
-
A.
2
-
B.
1
-
C.
-1
-
D.
-2
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Giá trị cực tiểu của hàm số là y = -2 tại x = -1.
Cho hàm số \(y = f(x) = \frac{{a{x^2} + bx + c}}{{x + d}}\) có đồ thị là đường cong trong hình vẽ dưới đây, biết đường tiệm cận xiên của đồ thị hàm số đi qua hai điểm (0;1) và (1;0).
a) Hàm số đồng biến trên khoảng (-4;0).
b) Ta có a + b + c + d = -2.
c) Khoảng cách từ M(1;-8) đến đường thẳng đi qua các điểm cực trị của đồ thị hàm số là \(\sqrt 5 \).
d) Tập xác định của hàm số là \(\mathbb{R}\backslash \{ 2\} \).
a) Hàm số đồng biến trên khoảng (-4;0).
b) Ta có a + b + c + d = -2.
c) Khoảng cách từ M(1;-8) đến đường thẳng đi qua các điểm cực trị của đồ thị hàm số là \(\sqrt 5 \).
d) Tập xác định của hàm số là \(\mathbb{R}\backslash \{ 2\} \).
Quan sát đồ thị, xét các điểm đồ thị đi qua và đường tiệm cận để tìm hàm số.
a) Sai. Hàm số không xác định trên khoảng (-4;0) nên không đồng biến trên khoảng (-4;0).
b) Đúng. Đường tiệm cận xiên dạng y = mx + n \((m \ne 0)\) của đồ thị hàm số đi qua hai điểm (0;1) và (1;0) nên ta có \(\left\{ \begin{array}{l}1 = m.0 + n\\0 = m.1 + n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 1\\n = 1\end{array} \right.\).
Do đó đường tiệm cận xiên có phương trình y= -x + 1, hệ số góc là m = -1.
Suy ra \(\frac{a}{1} = - 1 \Leftrightarrow a = - 1\).
Đường tiệm cận đứng có phương trình x = -2, suy ra d = 2.
Ta có \(y = f(x) = \frac{{ - {x^2} + bx + c}}{{x + 2}}\) đi qua hai điểm có tọa độ (0;-1), (-4;7) nên:
\(\left\{ \begin{array}{l}\frac{{ - {0^2} + b.0 + c}}{{0 + 2}} = - 1\\\frac{{ - {{( - 4)}^2} + b.( - 4) + c}}{{( - 4) + 2}} = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{c}{2} = - 1\\\frac{{ - 16 - 4b + c}}{{ - 4 + 2}} = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = - 2\\b = - 1\end{array} \right.\).
Vậy a + b + c + d = -1 + (-1) + (-2) + 2 = -2.
c) Đúng. Hai điểm cực trị của hàm số là A(-1;0) và B(-4;7) nên đường thẳng AB có phương trình \(y = - 2x - 1 \Leftrightarrow 2x + y + 1 = 0\).
Khoảng cách từ M đến đường thẳng AB là \(d(M,AB) = \frac{{\left| {2 - 8 + 1} \right|}}{{\sqrt {4 + 1} }} = \sqrt 5 \).
d) Sai. Hàm số \(y = f(x) = \frac{{ - {x^2} - x - 2}}{{x + 2}}\) có tập xác định là \(D = \mathbb{R}\backslash \{ - 2\} \).
Cho hàm số \(y = f(x) = {e^{x + \sqrt {16 - {x^2}} }}\).
a) f’(x) = 0 có hai nghiệm phân biệt.
b) \(f'(x) = \left( {1 - \frac{x}{{\sqrt {16 - {x^2}} }}} \right){e^{x + \sqrt {16 - {x^2}} }}\), \(\forall x \in [ - 4;4]\).
c) Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) là \({e^{a + b\sqrt c }}\) (với \(a,b,c \in \mathbb{Z}\) và c là số nguyên tố). Khi đó a + 2b + 3c = 10.
d) \(f( - 4) = \frac{1}{{{e^4}}}\).
a) f’(x) = 0 có hai nghiệm phân biệt.
b) \(f'(x) = \left( {1 - \frac{x}{{\sqrt {16 - {x^2}} }}} \right){e^{x + \sqrt {16 - {x^2}} }}\), \(\forall x \in [ - 4;4]\).
c) Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) là \({e^{a + b\sqrt c }}\) (với \(a,b,c \in \mathbb{Z}\) và c là số nguyên tố). Khi đó a + 2b + 3c = 10.
d) \(f( - 4) = \frac{1}{{{e^4}}}\).
Tính đạo hàm f’(x) của hàm số theo quy tắc đạo hàm hàm số hợp \(\left( {{e^u}} \right)' = u'.{e^u}\).
Tìm nghiệm của phương trình f’(x) = 0.
a) Sai. \(f'(x) = \left( {x + \sqrt {16 - {x^2}} } \right)'{e^{x + \sqrt {16 - {x^2}} }} = \left( {1 + \frac{{\left( {16 - {x^2}} \right)'}}{{2\sqrt {16 - {x^2}} }}} \right){e^{x + \sqrt {16 - {x^2}} }}\)
\( = \left( {1 + \frac{{ - 2x}}{{2\sqrt {16 - {x^2}} }}} \right){e^{x + \sqrt {16 - {x^2}} }} = \left( {1 - \frac{x}{{\sqrt {16 - {x^2}} }}} \right){e^{x + \sqrt {16 - {x^2}} }}\) với \(16 - {x^2} > 0 \Leftrightarrow - 4 < x < 4\).
\(f'(x) = 0 \Leftrightarrow \left( {1 - \frac{x}{{\sqrt {16 - {x^2}} }}} \right){e^{x + \sqrt {16 - {x^2}} }} = 0 \Leftrightarrow 1 - \frac{x}{{\sqrt {16 - {x^2}} }} = 0 \Leftrightarrow \left\{ \begin{array}{l}\sqrt {16 - {x^2}} = x\\16 - {x^2} > 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x > 0\\ - 4 < x < 4\\2{x^2} - 16 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x < 4\\2{x^2} - 16 = 0\end{array} \right. \Leftrightarrow x = 2\sqrt 2 \).
Vậy phương trình f’(x) = 0 có một nghiệm.
b) Sai. \(f'(x) = \left( {1 - \frac{x}{{\sqrt {16 - {x^2}} }}} \right){e^{x + \sqrt {16 - {x^2}} }}\) với \(x \in ( - 4;4)\).
c) Đúng. \(y = f(x)\) liên tục trên đoạn [-4;4]; f’(x) = 0 có một nghiệm \(x = 2\sqrt 2 \) trên khoảng (-4;4).
\(f( - 4) = {e^{ - 4}}\); \(f(2\sqrt 2 ) = {e^{4\sqrt 2 }}\); \(f(4) = {e^4}\).
Suy ra \(\mathop {\min }\limits_{[ - 4;4]} f(x) = f( - 4) = {e^{ - 4}}\); \(\mathop {\max }\limits_{[ - 4;4]} f(x) = f(2\sqrt 2 ) = {e^{4\sqrt 2 }}\).
Ta có \({e^{ - 4}}.{e^{4\sqrt 2 }} = {e^{ - 4 + 4\sqrt 2 }} \Rightarrow \left\{ \begin{array}{l}a = - 4\\b = 4\\c = 2\end{array} \right. \Rightarrow a + 2b + 3c = - 4 + 2.4 + 3.2 = 10\).
d) Đúng. \(f( - 4) = {e^{ - 4}} = \frac{1}{{{e^4}}}\).
Một hạt chuyển động trên một đường thẳng có gắn một trục tọa độ với gốc tọa độ là vị trí hạt bắt đầu chuyển động. Tọa độ của hạt trên trục tại thời điểm t (đơn vị: giây) kể từ khi xuất phát được cho bởi công thức x(t) = 2t – 3ln(t + 1) (đơn vị: mét), \(t \ge 0\). Hàm số v(t) = x’(t) (đơn vị: mét/giây) biểu thị vận tốc chuyển động của hạt.
a) Quãng đường mà hạt đi được trong 3 giây đầu tiên là 1,84 m (làm tròn kết quả đến hàng phần trăm).
b) Hạt đứng yên tại thời điểm t = 0,5 s.
c) \(v(t) = 2 - \frac{3}{{t + 1}}\).
d) Vận tốc ban đầu của hạt là 1 m/s.
a) Quãng đường mà hạt đi được trong 3 giây đầu tiên là 1,84 m (làm tròn kết quả đến hàng phần trăm).
b) Hạt đứng yên tại thời điểm t = 0,5 s.
c) \(v(t) = 2 - \frac{3}{{t + 1}}\).
d) Vận tốc ban đầu của hạt là 1 m/s.
x’(t) = v(t).
a) Sai. \(v(t) = x'(t) = 2 - \frac{3}{{t + 1}}\).
\(v(t) = 0 \Leftrightarrow 2 - \frac{3}{{t + 1}} = 0 \Leftrightarrow t = \frac{1}{2}\).
Quãng đường hạt đi được trong 3 giây đầu là:
\(2\left| {x\left( {\frac{1}{2}} \right)} \right| + x(3) = 1\left| {1 - 3\ln \frac{3}{2}} \right| + 6 - 3\ln 4 = 4 + 6\ln \frac{3}{2} - 3\ln 4 \approx 2,27\) (m).
b) Đúng. Hạt đứng yên khi \(v(t) = 2 - \frac{3}{{t + 1}} = 0 \Leftrightarrow t = 0,5\) (s).
c) Đúng. \(v(t) = x'(t) = 2 - \frac{3}{{t + 1}}\).
d) Sai. Vận tốc ban đầu của hạt là \(v(0) = 2 - \frac{3}{{0 + 1}} = - 1\) (m/s).
Một kho chứa hàng có dạng hình lăng trụ đứng ABFPE.DCGQH với ABFE là hình chữ nhật và
EFP là tam giác cân tại P. Gọi T là trung điểm của DC. Các kích thước của kho chứa lần lượt là
AB = 6 m; AE = 5 m; AD = 8 m; QT = 7 m. Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có
gốc toạ độ là điểm O thuộc đoạn AD sao cho OA = 2 m và các trục toạ độ tương ứng như hình vẽ dưới đây.
a) Tọa độ điểm Q là (-6;3;5).
b) Vecto \(\overrightarrow {OC} \) có tọa độ là (-6;6;0).
c) Người ta muốn lắp camera quan sát trong nhà kho tại vị trí trung điểm của FG và đầu thu dữ liệu đặt tại vị trí O. Người ta thiết kế đường dây cáp nối từ O đến K sau đó nối thẳng đến camera. Độ dài đoạn cáp nối tối thiểu bằng \(5 + 2\sqrt {10} \) m.
d) Mái nhà được lợp bằng tôn Hoa Sen, giá tiền mỗi mét vuông tôn là 130000 đồng. Số tiền cần bỏ ra để mua tôn lợp mái nhà là 3750000 đồng (không kể hao phí do việc cắt và ghép các miếng tôn, làm tròn kết quả đến hàng nghìn).
a) Tọa độ điểm Q là (-6;3;5).
b) Vecto \(\overrightarrow {OC} \) có tọa độ là (-6;6;0).
c) Người ta muốn lắp camera quan sát trong nhà kho tại vị trí trung điểm của FG và đầu thu dữ liệu đặt tại vị trí O. Người ta thiết kế đường dây cáp nối từ O đến K sau đó nối thẳng đến camera. Độ dài đoạn cáp nối tối thiểu bằng \(5 + 2\sqrt {10} \) m.
d) Mái nhà được lợp bằng tôn Hoa Sen, giá tiền mỗi mét vuông tôn là 130000 đồng. Số tiền cần bỏ ra để mua tôn lợp mái nhà là 3750000 đồng (không kể hao phí do việc cắt và ghép các miếng tôn, làm tròn kết quả đến hàng nghìn).
Tìm tọa độ các điểm cần thiết để tính toán.
Từ các dữ kiện của bài toán ta có toạ độ các điểm A(2;0;0), D(-6;0;0), B(2;6;0), E(2;0;5) C(-6;6;0).
a) Sai. Hình chiếu của Q lên mặt phẳng (Oxy) là T(-6;3;0) và QT = 7 nên có Q(-6;3;7).
b) Đúng. \(\overrightarrow {OC} = ( - 6 - 0;6 - 0;0 - 0) = ( - 6;6;0)\).
c) Đúng. Có K(0;0;5), F(2;6;5), G(-6;6;5). Gọi I là vị trí đạt camera, khi đó I là trung điểm của FG nên:
\(\left\{ \begin{array}{l}{x_I} = \frac{{{x_F} + {x_G}}}{2} = \frac{{2 - 6}}{2} = - 2\\{y_I} = \frac{{{y_F} + {y_G}}}{2} = \frac{{6 + 6}}{2} = 6\\{z_I} = \frac{{{z_F} + {z_G}}}{2} = \frac{{5 + 5}}{2} = 5\end{array} \right. \Rightarrow I( - 2;6;5)\).
Độ dài đoạn cáp tối thiểu là \(OK + KI = 5 + \sqrt {{{( - 2 - 0)}^2} + {{(6 - 0)}^2} + {{(5 - 5)}^2}} = 5 + 2\sqrt {10} \) (m).
d) Sai. Có H(-6;0;5), Q(-6;3;7) nên \(QH = \sqrt {13} \).
Diện tích mái tôn là \(S = 2HQ.EH = 16\sqrt {13} \) \(({m^2})\).
Số tiền cần bỏ ra là \(16\sqrt {13} .130000 \approx 7500000\) (đồng).
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thoi tâm O, SO vuông góc với mặt đáy. Biết cạnh hình thoi bằng 2024, góc BAD bằng \({120^o}\), khoảng cách từ điểm C đến mặt phẳng (SBD) bằng bao nhiêu?
Đáp án:
Đáp án:
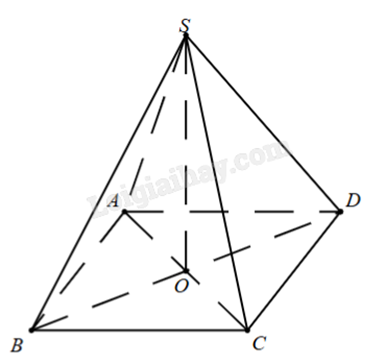
Ta có \(\left\{ \begin{array}{l}SO \bot (ABCD) \Rightarrow SO \bot OC\\AC \bot BD \Rightarrow OC \bot BD\end{array} \right. \Rightarrow OC \bot (SBD)\).
Mà O thuộc (SBD) nên \(d(C,(SBD)) = OC\).
Vì \(\widehat {BAD} = {120^o}\) nên \(\widehat {BAC} = \widehat {DAC} = {60^o}\). Do đó tam giác ABC là tam giác đều và AC = AB = 2024.
Vậy \(d(C,(SBD)) = OC = \frac{{AC}}{2} = \frac{{2024}}{2} = 1012\).
Trong không gian Oxyz, một khinh khí cầu ở tọa độ A(-16;-10;10) bắt đầu bay với vecto vận tốc
không đổi \(\overrightarrow v = (4;3; - 1)\) (đơn vị vận tốc là km/h) và dự kiến bay trong thời gian 10 giờ. Biết trạm kiểm soát không lưu đặt ở vị trí gốc toạ độ O kiểm soát được các vật thể cách trạm một khoảng tối đa bằng 12 km. Thời gian kể từ khi trạm kiểm soát không lưu phát hiện ra khinh khí cầu đến khi khinh khí cầu ra khỏi vùng kiểm soát là bao nhiêu phút?
Đáp án:
Đáp án:
Biểu diễn tọa độ vị trí M của khinh khí cầu theo thời gian t. Tìm điều kiện của t sao cho khoảng cách OM nhỏ hơn hoặc bằng 12.
Ta có sau khoảng thời gian t (h) khinh khí cầu đang ở vị trí M thì toạ độ M được xác định bởi:
\(\overrightarrow {AM} = t\overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_M} - {x_A} = 4t\\{y_M} - {y_A} = 3t\\{z_M} - {z_A} = - t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 4t + {x_A} = 4t - 16\\{y_M} = 3t + {y_A} = 3t - 10\\{z_M} = - t + {z_A} = - t + 10\end{array} \right. \Rightarrow M(4t - 16;3t - 10; - t + 10)\)
Để hệ thống kiểm soát không lưu quan sát được khinh khí cầu ở vị trí M thì:
\(OM \le 12 \Leftrightarrow \sqrt {{{( - 16 + 4t)}^2} + {{( - 10 + 3t)}^2} + {{(10 - t)}^2}} \le 12 \Leftrightarrow \sqrt {456 - 208t + 26{t^2}} \le 12 \Leftrightarrow 2 \le t \le 6\).
Do đó hệ thống kiểm soát không lưu có thể quan sát khinh khí cầu trong khoảng thời gian 4 giờ hay 240 phút.
Một thanh dầm hình hộp chữ nhật được cắt từ một khúc gỗ hình trụ có bán kính đáy bằng 20 cm sao cho thanh dầm có diện tích mặt cắt ngang lớn nhất, tức là thanh dầm có mặt cắt ngang là hình vuông. Sau khi cắt thanh dầm đó, người ta lại cắt bốn tấm ván hình hộp chữ nhật từ bốn phần còn lại của khúc gỗ (tham khảo hình vẽ dưới đây). Xác định diện tích mặt cắt ngang tối đa của mỗi tấm ván (theo đơn vị \(c{m^2}\) và làm tròn kết quả đến hàng phần chục).
Đáp án:
Đáp án:
Lập hàm số biểu diễn diện tích của mặt cắt ngang thông qua biến x. Tìm giá trị lớn nhất của hàm số vừa lập với điều kiện của x.
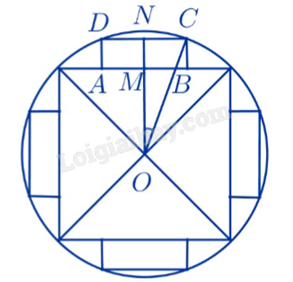
Gọi mặt cắt ngang của tấm ván là hình chữ nhật ABCD; M, N lần lượt là trung điểm của AB, CD.
Hình vuông có đường chéo dài 20 cm có độ dài cạnh là \(\frac{{40}}{{\sqrt 2 }} = 20\sqrt 2 \) cm.
Đặt MN = x (cm), \(OM = \frac{1}{2}.20\sqrt 2 = 10\sqrt 2 \) (cm). Khi đó: \(ON = x + 10\sqrt 2 \)(cm).
\(NC = \sqrt {O{C^2} - O{N^2}} = \sqrt {{{20}^2} - {{\left( {x - 10\sqrt 2 } \right)}^2}} = \sqrt { - {x^2} - 20\sqrt 2 x + 200} \)
\( \Rightarrow AB = 2NC = 2\sqrt { - {x^2} - 20\sqrt 2 x + 200} \) \((0 < x < 20 - 10\sqrt 2 )\).
Diện tích mặt cắt ngang hình chữ nhật của tấm ván là:
\(S = AB.MN = 2x\sqrt { - {x^2} - 20\sqrt 2 x + 200} = 2\sqrt { - {x^4} - 20\sqrt 2 {x^3} + 200{x^2}} \).
\(S' = \frac{{ - 4{x^3} - 60\sqrt 2 {x^2} + 400x}}{{\sqrt { - {x^4} - 20\sqrt 2 {x^3} + 200{x^2}} }}\); \(S' = 0 \Leftrightarrow - 4{x^3} - 60\sqrt 2 {x^2} + 400x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{5\sqrt {34} - 15\sqrt 2 }}{2}\\x = \frac{{ - 5\sqrt {34} - 15\sqrt 2 }}{2}\end{array} \right.\).
Kết hợp ĐK, ta có \(x = \frac{{5\sqrt {34} - 15\sqrt 2 }}{2}\) thỏa mãn.
Bảng biến thiên:
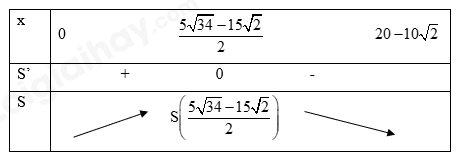
Vậy diện tích mặt cắt lớn nhất là \(S\left( {\frac{{5\sqrt {34} - 15\sqrt 2 }}{2}} \right) \approx 67,3\) \((c{m^2})\).
Trong một chiếc hộp có 30 viên bi có cùng kích thước và khối lượng, trong đó có 6 viên bi màu đỏ, 7 viên bi màu xanh, 8 viên bi màu vàng và 9 viên bi màu trắng. Lấy ngẫu nhiên đồng thời 3 viên bi. Xác suất để 3 viên bi lấy ra có đúng hai màu bằng \(\frac{a}{b}\), với \(\frac{a}{b}\) là phân số tối giản. Tổng a + b bằng bao nhiêu?
Đáp án:
Đáp án:
Sử dụng công thức tổ hợp.
Chia các trường hợp cụ thể và tính số cách chọn cho từng trường hợp.
Số cách chọn 3 viên bi bất kì là: \(C_{30}^3 = 4060\).
Số cách chọn 3 viên bi sao cho có 1 viên đỏ và 2 viên còn lại cùng màu là: \(6.(C_7^2 + C_8^2 + C_9^2) = 510\).
Số cách chọn 3 viên bi sao cho có 1 viên xanh và 2 viên còn lại cùng màu là: \(7.(C_6^2 + C_8^2 + C_9^2) = 553\).
Số cách chọn 3 viên bi sao cho có 1 viên vàng và 2 viên còn lại cùng màu là: \(8.(C_7^2 + C_6^2 + C_9^2) = 576\).
Số cách chọn 3 viên bi sao cho có 1 viên trắng và 2 viên còn lại cùng màu là: \(9.(C_7^2 + C_8^2 + C_6^2) = 576\).
Tổng số cách chọn 3 viên bi sao cho có đúng hai màu là: 510 + 553 + 576 + 576 = 2215.
Xác suất để 3 viên bi lấy ra có đúng hai màu là: \(\frac{{2215}}{{4060}} = \frac{{443}}{{812}}\) nên a + b = 443 + 812 = 1255.
Một nhà máy sản xuất x sản phẩm trong mỗi tháng. Chi phí sản xuất x sản phẩm được cho bởi hàm chi phí \(C(x) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}\) (nghìn đồng). Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm x và được cho bởi công thức \(p(x) = 1700 - 7x\) (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.
Đáp án:
Đáp án:
Lập hàm số biểu diễn lợi nhuận của công ty theo biến x. Tìm giá trị lớn nhất của hàm số và kết luận giá trị x tương ứng.
Điều kiện: \(\left\{ \begin{array}{l}x > 0\\1700 - 7x > 0\end{array} \right. \Leftrightarrow 0 < x < \frac{{1700}}{7}\).
Doanh thu của công ty tiêu thụ hết x sản phẩm là \(R(x) = xp(x) = 1700x - 7{x^2}\).
Lợi nhuận của công ty khi bán hết x sản phẩm là \(P(x) = R(x) - C(x) = 1700x - 7{x^2} - \left( {16000 + 500x - 1,6{x^2} + 0,004{x^3}} \right)\)
\( = - 0,004{x^3} - 5,4{x^2} + 1200x - 16000\) \(\left( {0 < x < \frac{{1700}}{7}} \right)\).
\(P'(x) = - 0,012{x^2} - 10,8x + 1200 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1000\\x = 100\end{array} \right.\).
Kết hợp ĐK, ta có x = 100 thỏa mãn.
Bảng biến thiên:
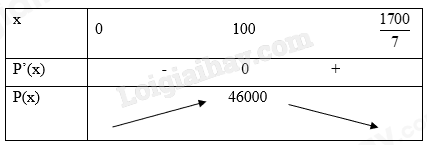
Vậy mỗi tháng nhà máy nên sản xuất 100 sản phẩm để lợi nhuận thu được là lớn nhất.
Một kỹ sư thiết kế mô hình trang trí cho một sân khấu nổi có dạng hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\) với độ dài các cạnh bằng 5 m. Để tạo ra nét độc đáo cho sân khấu, người kỹ sư muốn thiết kế một dàn đèn ánh sáng nối từ một điểm M trên đường chéo \(A{D_1}\) xuống một điểm N trên mặt đất BD đồng thời AM = DB. Dàn đèn ánh sáng có chiều dài ngắn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm).
Đáp án:
Đáp án:
Sử dụng phương pháp tọa độ hóa và ứng dụng đạo hàm để tìm giá trị nhỏ nhất.
Chọn hệ trục tọa độ Oxyz có gốc O trùng với điểm A, B thuộc tia Ox, D thuộc tia Oy, \({A_1}\) thuộc tia Oz.
Đặt \(AM = DN = x\sqrt 2 \).
Ứng dụng hệ thức lượng trong tam giác vuông, ta tính được M(0;x;x) và N(x;5 – x;0).
Khi đó \(M{N^2} = {(x - 0)^2} + {(5 - x - x)^2} + {(0 - x)^2} = 6{x^2} - 20x + 25 = f(x)\).
\(f'(x) = 12x - 20 = 0 \Leftrightarrow x = \frac{5}{3}\).
Vậy dàn đèn có chiều dài ngắn nhất bằng \(f\left( {\frac{5}{3}} \right) = \frac{{5\sqrt 3 }}{3} \approx 2,89\).
Các bài khác cùng chuyên mục
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Ninh Bình
- Đề thi thử THPT môn Toán năm 2025 Sở GD Hà Tĩnh
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Vĩnh Phúc
- Đề tham khảo thi THPT môn Toán - Đề số 3 (hay, chi tiết)
- Đề tham khảo thi THPT môn Toán - Đề số 2 (hay, chi tiết)
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Ninh Bình
- Đề thi thử THPT môn Toán năm 2025 Sở GD Hà Tĩnh
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Vĩnh Phúc
- Đề tham khảo thi THPT môn Toán - Đề số 3 (hay, chi tiết)
- Đề tham khảo thi THPT môn Toán - Đề số 2 (hay, chi tiết)
