Đề tham khảo thi THPT môn Toán - Đề số 9 (hay, chi tiết)
I. Phần trắc nghiệm
Đề bài
Trong không gian Oxyz, cho điểm A(2;3;1) và vecto \(\overrightarrow n = \left( {1;2; - 3} \right)\). Viết phương trình mặt phẳng \((\alpha )\) qua A và nhận vecto \(\overrightarrow n \) làm vectơ pháp tuyến.
-
A.
\(x + 2y - 3z - 5 = 0\)
-
B.
\(x + 2y - 3z + 7 = 0\)
-
C.
\(2x + 4y - 6z + 5 = 0\)
-
D.
\(x + 5y - 6z + 5 = 0\)
Tính đạo hàm của hàm số \(f\left( x \right) = {{\rm{e}}^{2x - 3}}\).
-
A.
\(f'\left( x \right) = 2.{{\rm{e}}^{2x - 3}}\)
-
B.
\(f'\left( x \right) = - 2.{{\rm{e}}^{2x - 3}}\)
-
C.
\(f'\left( x \right) = 2.{{\rm{e}}^{x - 3}}\)
-
D.
\(f'\left( x \right) = {{\rm{e}}^{2x - 3}}\)
Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2,\) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 2\) và \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 3\). Khi đó đồ thị có
-
A.
Tiệm cận đứng x = 3
-
B.
Một tiệm cận
-
C.
Không tiệm cận
-
D.
Hai tiệm cận y = 2; y = -2
Cho tập hợp A có 20 phần tử, số tập con có hai phần tử của A là
-
A.
\(2C_{20}^2\)
-
B.
\(2A_{20}^2\)
-
C.
\(C_{20}^2\)
-
D.
\(A_{20}^2\)
Cho cấp số cộng với \({u_3} = 8\), d = 2. Khi đó \({u_5}\) là
-
A.
6
-
B.
10
-
C.
12
-
D.
4
Một bệnh viện thống kê lại số cân nặng của 20 bé sơ sinh trong bảng sau:

Phương sai của mẫu số liệu ghép nhóm là
-
A.
3,39
-
B.
11,62
-
C.
0,1314
-
D.
0,36
Phương trình \({\left( {\frac{1}{4}} \right)^x} = {2^{{x^2} - 5x + 2}}\) có nghiệm là
-
A.
x = 2; x = 3
-
B.
x = 1; x = 3
-
C.
x = 1; x = 2
-
D.
x = 1; x = -2
Cho khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \), khoảng cách giữa hai đáy của lăng trụ bằng \(a\sqrt 6 .\) Tính thể tích V của khối lăng trụ.
-
A.
\(V = 3{a^3}\sqrt 2 \)
-
B.
\(V = {a^3}\sqrt 2 \)
-
C.
\(V = \frac{{{a^3}\sqrt 2 }}{3}\)
-
D.
\(V = \frac{{3{a^3}\sqrt 2 }}{4}\)
Cho \(\overrightarrow {AB} = \left( {1;3;2} \right)\). Tọa độ của \(\overrightarrow a = 2\overrightarrow {AB} \) là
-
A.
\(\left( {2;6;4} \right)\)
-
B.
\(\left( {2;3;4} \right)\)
-
C.
\(\left( {2;6;2} \right)\)
-
D.
\(\left( {1;6;4} \right)\)
Cho mẫu số liệu ghép nhóm của chiều cao của cây cao su trong một nông trường:

Trung vị của mẫu số liệu trên là
-
A.
\(\frac{{1121}}{{60}}\)
-
B.
\(\frac{{75}}{4}\)
-
C.
\(\frac{{1127}}{{60}}\)
-
D.
\(\frac{{1123}}{{60}}\)
Trong không gian (Oxyz), cho hai mặt phẳng (P): x – 2y – z + 1 = 0, (Q): x + y + 2z + 7 = 0. Tính góc giữa hai mặt phẳng đó.
-
A.
\({60^o}\)
-
B.
\({45^o}\)
-
C.
\({120^o}\)
-
D.
\({30^o}\)
Trong không gian (Oxyz), cho mặt cầu có tâm I(1;2;4) và bán kính R = 5. Khi đó mặt cầu có phương trình là
-
A.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 4} \right)^2} = 5\)
-
B.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 4} \right)^2} = 25\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 4} \right)^2} = 5\)
-
D.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 4} \right)^2} = 25\)
Cho hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\)có đồ thị như hình vẽ.
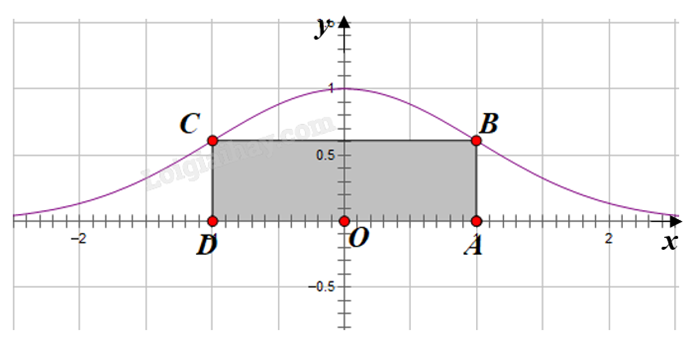
Biết ABCD là hình chữ nhật thay đổi sao cho hai điểm B, C luôn thuộc đồ thị hàm số đã cho. Hai điểm A, D nằm trên trục hoành (điểm A thuộc tia Ox).
a) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).
b) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y' = f'\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
c) Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với \(x > 0\) thì diện tích ABCD là \(S\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
d) Diện tích hình chữ nhật ABCD đạt giá trị lớn nhất khi AD = 2.
Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia tốc phụ thuộc vào thời gian t(s) là a(t) = 2t – 7 \(\left( {m/{s^2}} \right)\) Biết vận tốc ban đầu bằng 6 (m/s).
a) Phương trình vận tốc của chất điểm tại tời điểm t được xác định bởi công thức \(v\left( t \right) = \int {a\left( t \right)} dt\).
b) Tại thời điểm t = 7 (s), vận tốc của chất điểm là 6 (m/s).
c) Độ dịch chuyển của vật trong khoảng thời gian \(1 \le t \le 7\) là 18 m.
d) Trong 8 giây đầu tiên, thời điểm chất điểm xa nhất về phía bên phải là t = 7 (s).
a) Tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 14\).
b) Tứ phân vị thứ ba của dãy số liệu là \({Q_3} = 11,5\).
c) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

d) Ước lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên ta được tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = 8,25\).
Cho hình chóp S.ABCD có đáy là hình chữ nhật có cạnh AB = 2a, AD = a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm AB và CD.
a) \(SH \bot (ABCD)\).
b) Góc giữa SC và (ABCD) là góc \(\widehat {SHC}\).
c) Góc phẳng nhị diện [S,AB,C] bằng \({90^o}\).
d) Góc phẳng nhị diện [S,CD,A] bằng \({45^o}\).
Cho hàm số \(y = {e^x}\left( {{x^2} - 3} \right)\), gọi \(M = \frac{a}{{{e^b}}}\) \(\left( {a \in \mathbb{N},b \in \mathbb{N}} \right)\) là giá trị lớn nhất của hàm số trên đoạn [-5;-2]. Tính giá trị của biểu thức P = a + b?
Đáp án:
Cho hình lăng trụ tam giác ABC.A’B’C’ đáy là tam giác vuông cân có cạnh huyền \(AB = \sqrt 8 \). Khoảng cách giữa hai đường thẳng AB và B’C’ bằng 3. Tính thể tích khối chóp B.ACC’A’.
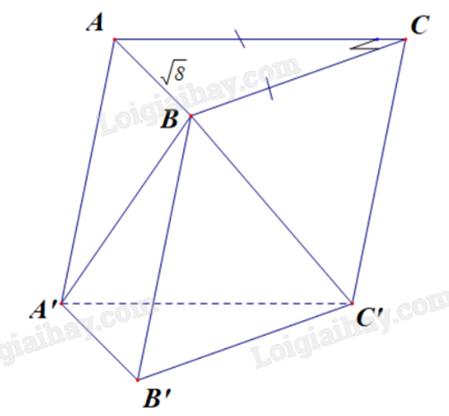
Đáp án:
Một căn phòng dạng hình hộp chữ nhật với chiều dài 8m, rộng 6m và cao 4m có hai chiếc quạt treo tường. Chiếc quạt A treo chính giữa bức tường 8m và cách trần 1m, chiếc quạt B treo chính giữa bức tường 6m và cách trần 1,5m. Hỏi khoảng cách giữa hai chiếc quạt AB cách nhau bao nhiêu m (làm tròn đến hàng phần nghìn)?
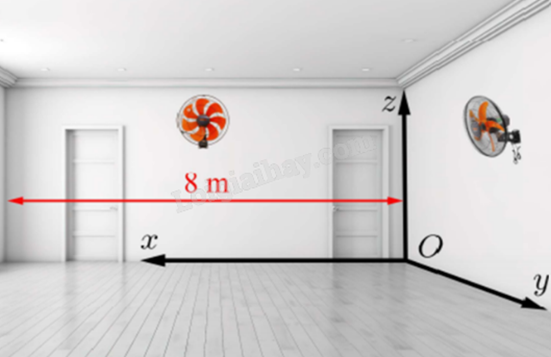
Đáp án:
Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc, xây dựng, thiết bị nội thất,... Một bồn rửa (lavabo) bằng sứ có hình dạng là một nửa khối tròn xoay khi elip quay quanh một trục (hình minh họa). Thông số kĩ thuật mặt trên của bồn rửa: dài \( \times \) rộng là \(660 \times 380{\rm{mm}},\) giả thiết bồn rửa có độ dày đồng đều \(\delta \) là \(20{\rm{mm}}\).
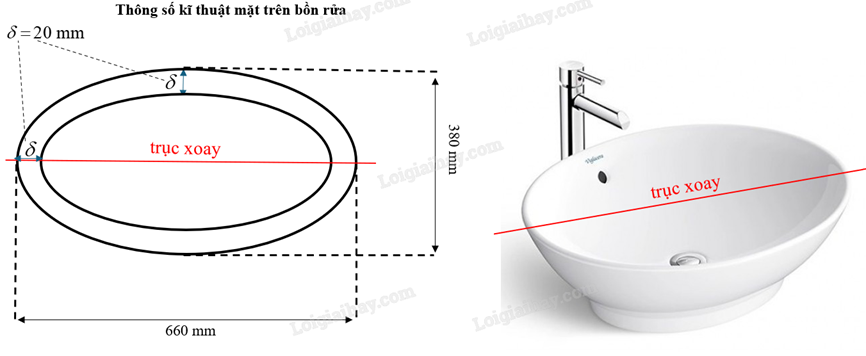
Thể tích chứa nước của bồn rửa bằng bao nhiêu decimet khối (làm tròn đến hàng phần trăm)?
Đáp án:
Sự chuyển động của máy bay A được thể hiện trong không gian Oxyz như sau: Máy bay khởi hành từ B(0;0;2) chuyển động thẳng đều (tính theo phút) với vận tốc được biểu thị theo vecto \(\overrightarrow v (1;4;5)\). Sau khi khởi hành được 30 phút, máy bay ở vị trí M(x;y;z). Tính P = 3x + y + z.
Đáp án:
Áo sơ mi G9 trước khi xuất khẩu sang Mỹ phải qua 2 lần kiểm tra, nếu cả hai lần đều đạt thì chiếc áo đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân 95% sản phẩm làm ra qua được lần kiểm tra thứ nhất, và 92% sản phẩm qua được lần kiểm tra đầu sẽ tiếp tục qua được lần kiểm tra thứ hai. Xác suất để 1 chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là \(\frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính a + b.
Đáp án:
Lời giải và đáp án
Trong không gian Oxyz, cho điểm A(2;3;1) và vecto \(\overrightarrow n = \left( {1;2; - 3} \right)\). Viết phương trình mặt phẳng \((\alpha )\) qua A và nhận vecto \(\overrightarrow n \) làm vectơ pháp tuyến.
-
A.
\(x + 2y - 3z - 5 = 0\)
-
B.
\(x + 2y - 3z + 7 = 0\)
-
C.
\(2x + 4y - 6z + 5 = 0\)
-
D.
\(x + 5y - 6z + 5 = 0\)
Đáp án : A
Phương trình mặt phẳng qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có vecto pháp tuyến \(\overrightarrow n = \left( {a;b;c} \right)\) là:
\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\).
Phương trình mặt phẳng qua A(2;3;1) và có vecto pháp tuyến \(\overrightarrow n = \left( {1;2; - 3} \right)\) là:
\(1\left( {x - 2} \right) + 2\left( {y - 3} \right) - 3\left( {z - 1} \right) = 0 \Leftrightarrow x + 2y - 3z - 5 = 0\).
Tính đạo hàm của hàm số \(f\left( x \right) = {{\rm{e}}^{2x - 3}}\).
-
A.
\(f'\left( x \right) = 2.{{\rm{e}}^{2x - 3}}\)
-
B.
\(f'\left( x \right) = - 2.{{\rm{e}}^{2x - 3}}\)
-
C.
\(f'\left( x \right) = 2.{{\rm{e}}^{x - 3}}\)
-
D.
\(f'\left( x \right) = {{\rm{e}}^{2x - 3}}\)
Đáp án : A
Áp dụng quy tắc đạo hàm của hàm hợp: \(\left( {{e^u}} \right)' = u'{e^u}\).
\(f'\left( x \right) = (2x - 3)'{{\rm{e}}^{2x - 3}} = 2{{\rm{e}}^{2x - 3}}\).
Cho hàm số \(y = f\left( x \right)\) có \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2,\) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 2\) và \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = 3\). Khi đó đồ thị có
-
A.
Tiệm cận đứng x = 3
-
B.
Một tiệm cận
-
C.
Không tiệm cận
-
D.
Hai tiệm cận y = 2; y = -2
Đáp án : D
\(x = {x_0}\) là tiệm cận đứng của đồ thị y = f(x) khi thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \).
\(y = {y_0}\) là tiệm cận ngang của đồ thị y = f(x) khi thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\); \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\).
Vì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2,\) \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 2\) nên đồ thị có hai tiệm cận ngang y = 2; y = -2.
Cho tập hợp A có 20 phần tử, số tập con có hai phần tử của A là
-
A.
\(2C_{20}^2\)
-
B.
\(2A_{20}^2\)
-
C.
\(C_{20}^2\)
-
D.
\(A_{20}^2\)
Đáp án : C
Áp dụng công thức tính số tổ hợp.
Số tập con có hai phần tử của \(A\) là \(C_{20}^2\).
Cho cấp số cộng với \({u_3} = 8\), d = 2. Khi đó \({u_5}\) là
-
A.
6
-
B.
10
-
C.
12
-
D.
4
Đáp án : C
Áp dụng công thức số hạng tổng quát của cấp số cộng: \({u_n} = {u_1} + (n - 1)d\).
Ta có \({u_3} = {u_1} + 2d \Leftrightarrow {u_1} = 4 \Rightarrow {u_5} = {u_1} + 4d = 12\).
Một bệnh viện thống kê lại số cân nặng của 20 bé sơ sinh trong bảng sau:

Phương sai của mẫu số liệu ghép nhóm là
-
A.
3,39
-
B.
11,62
-
C.
0,1314
-
D.
0,36
Đáp án : C
Lập bảng tần số theo giá trị đại diện, tính số trung bình rồi tính phương sai.

Số trung bình: \(\overline {\rm{x}} = \frac{{3.2,85 + 6.3,15 + 5.3,45 + 4.3,75 + 2.4,05}}{{20}} = 3,39\).
Phương sai: \({s^2} = \frac{{3.2,{{85}^2} + 6.3,{{15}^2} + 5.3,{{45}^2} + 4.3,{{75}^2} + 2.4,{{05}^2}}}{{20}} - 3,{39^2} = 0,1314\).
Phương trình \({\left( {\frac{1}{4}} \right)^x} = {2^{{x^2} - 5x + 2}}\) có nghiệm là
-
A.
x = 2; x = 3
-
B.
x = 1; x = 3
-
C.
x = 1; x = 2
-
D.
x = 1; x = -2
Đáp án : C
Đưa hai vế về cùng cơ số.
ĐKXĐ: \(x \in \mathbb{R}\).
Ta có: \({\left( {\frac{1}{4}} \right)^x} = {2^{{x^2} - 5x + 2}} \Leftrightarrow {2^{ - 2x}} = {2^{{x^2} - 5x + 2}} \Leftrightarrow - 2x = {x^2} - 5x + 2 \)
\(\Leftrightarrow - {x^2} + 3x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\).
Cho khối lăng trụ có diện tích đáy bằng \({a^2}\sqrt 3 \), khoảng cách giữa hai đáy của lăng trụ bằng \(a\sqrt 6 .\) Tính thể tích V của khối lăng trụ.
-
A.
\(V = 3{a^3}\sqrt 2 \)
-
B.
\(V = {a^3}\sqrt 2 \)
-
C.
\(V = \frac{{{a^3}\sqrt 2 }}{3}\)
-
D.
\(V = \frac{{3{a^3}\sqrt 2 }}{4}\)
Đáp án : A
Áp dụng công thức V = Bh tính thể tích khối lăng có diện tích đáy là B, chiều cao là h.
\(V = Bh = {a^2}\sqrt 3 .a\sqrt 6 = 3{a^3}\sqrt 2 \).
Cho \(\overrightarrow {AB} = \left( {1;3;2} \right)\). Tọa độ của \(\overrightarrow a = 2\overrightarrow {AB} \) là
-
A.
\(\left( {2;6;4} \right)\)
-
B.
\(\left( {2;3;4} \right)\)
-
C.
\(\left( {2;6;2} \right)\)
-
D.
\(\left( {1;6;4} \right)\)
Đáp án : A
Áp dụng biểu thức tọa độ nhân vecto với một số: \(\overrightarrow u = (a;b;c) \Rightarrow k\overrightarrow u = (ka;kb;kc)\).
\(\overrightarrow a = 2\overrightarrow {AB} = \left( {2.1;2.3;2.2} \right) = \left( {2;6;4} \right)\).
Cho mẫu số liệu ghép nhóm của chiều cao của cây cao su trong một nông trường:

Trung vị của mẫu số liệu trên là
-
A.
\(\frac{{1121}}{{60}}\)
-
B.
\(\frac{{75}}{4}\)
-
C.
\(\frac{{1127}}{{60}}\)
-
D.
\(\frac{{1123}}{{60}}\)
Đáp án : D
Tìm cỡ mẫu rồi áp dụng công thức tính trung vị của mẫu số liệu ghép nhóm.
Ta có: \(n = 55 + 78 + 120 + 45 + 11 = 309\).
Trung vị: \({Q_2} = {x_{155}} \in \left[ {18;22} \right)\): \({Q_2} = 18 + \left( {22 - 18} \right).\frac{{\frac{{309.2}}{4} - 55 - 78}}{{120}} = \frac{{1123}}{{60}}\).
Trong không gian (Oxyz), cho hai mặt phẳng (P): x – 2y – z + 1 = 0, (Q): x + y + 2z + 7 = 0. Tính góc giữa hai mặt phẳng đó.
-
A.
\({60^o}\)
-
B.
\({45^o}\)
-
C.
\({120^o}\)
-
D.
\({30^o}\)
Đáp án : A
Áp dụng công thức tính góc giữa hai mặt phẳng (P), (Q): \(\cos \alpha = \frac{{\left| {{{\vec n}_P}.{{\vec n}_Q}} \right|}}{{\left| {{{\vec n}_P}} \right|.\left| {{{\vec n}_Q}} \right|}}\).
\(\overrightarrow {{n_P}} \left( {1\,;\, - 2\,;\, - 1} \right)\) là một vecto pháp tuyến của (P).
\(\overrightarrow {{n_Q}} \left( {1\,;\,1\,;\,2} \right)\) là một vecto pháp tuyến của (Q).
Gọi \(\alpha \) là góc giữa hai mặt phẳng (P) và (Q) \( \Rightarrow \cos \alpha = \frac{{\left| {{{\vec n}_P}.{{\vec n}_Q}} \right|}}{{\left| {{{\vec n}_P}} \right|.\left| {{{\vec n}_Q}} \right|}} = \frac{{\left| {1 - 2 - 2} \right|}}{{\sqrt 6 .\sqrt 6 }} = \frac{1}{2} \Rightarrow \alpha = {60^o}\).
Trong không gian (Oxyz), cho mặt cầu có tâm I(1;2;4) và bán kính R = 5. Khi đó mặt cầu có phương trình là
-
A.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 4} \right)^2} = 5\)
-
B.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 4} \right)^2} = 25\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 4} \right)^2} = 5\)
-
D.
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 4} \right)^2} = 25\)
Đáp án : B
Phương trình đường tròn tâm I(a;b;c) bán kính R = 5 là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Mặt cầu có tâm I(1;2;4) và bán kính R = 5 có phương trình là:
\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 4} \right)^2} = {5^2} \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 4} \right)^2} = 25\).
Cho hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\)có đồ thị như hình vẽ.

Biết ABCD là hình chữ nhật thay đổi sao cho hai điểm B, C luôn thuộc đồ thị hàm số đã cho. Hai điểm A, D nằm trên trục hoành (điểm A thuộc tia Ox).
a) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).
b) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y' = f'\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
c) Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với \(x > 0\) thì diện tích ABCD là \(S\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
d) Diện tích hình chữ nhật ABCD đạt giá trị lớn nhất khi AD = 2.
a) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).
b) Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y' = f'\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
c) Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với \(x > 0\) thì diện tích ABCD là \(S\left( x \right) = x{e^{ - \frac{1}{2}{x^2}}}\).
d) Diện tích hình chữ nhật ABCD đạt giá trị lớn nhất khi AD = 2.
Tìm tập xác định, tính đạo hàm rồi lập bảng biến thiên, tìm giá trị lớn nhất.
a) Đúng. Hàm số mũ \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có tập xác định \(D = \mathbb{R}\).
b) Sai. Hàm số \(y = f\left( x \right) = {e^{ - \frac{1}{2}{x^2}}}\) có đạo hàm là \(y'\, = {\left( { - \frac{1}{2}{x^2}} \right)^\prime }{e^{ - \frac{1}{2}{x^2}}} = - x{e^{ - \frac{1}{2}{x^2}}}\).
c) Sai. Khi điểm B có toạ độ \(\left( {x;{e^{ - \frac{1}{2}{x^2}}}} \right)\) với x > 0 thì cạnh AD = 2x, cạnh \(AB = {e^{ - \frac{1}{2}{x^2}}}\).
Diện tích hình chữ nhật ABCD được tính theo công thức \(S\left( x \right) = 2x{e^{ - \frac{1}{2}{x^2}}}\).
d) Đúng. Xét hàm số \(S\left( x \right) = 2x{e^{ - \frac{1}{2}{x^2}}}\) trên khoảng \(\left( {0; + \infty } \right)\).
\(S'\left( x \right) = 2{e^{ - \frac{1}{2}{x^2}}} - 2{x^2}{e^{ - \frac{1}{2}{x^2}}} = 2{e^{ - \frac{1}{2}{x^2}}}\left( {1 - {x^2}} \right) = 0 \Leftrightarrow 1 - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\).
Bảng biến thiên:
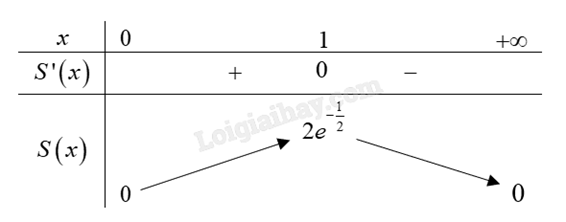
Hàm số S(x) đạt giá trị lớn nhất khi x = 1. Khi đó AD = 2.
Một chất điểm chuyển động trên đường thẳng nằm ngang (chiều dương hướng sang phải) với gia tốc phụ thuộc vào thời gian t(s) là a(t) = 2t – 7 \(\left( {m/{s^2}} \right)\) Biết vận tốc ban đầu bằng 6 (m/s).
a) Phương trình vận tốc của chất điểm tại tời điểm t được xác định bởi công thức \(v\left( t \right) = \int {a\left( t \right)} dt\).
b) Tại thời điểm t = 7 (s), vận tốc của chất điểm là 6 (m/s).
c) Độ dịch chuyển của vật trong khoảng thời gian \(1 \le t \le 7\) là 18 m.
d) Trong 8 giây đầu tiên, thời điểm chất điểm xa nhất về phía bên phải là t = 7 (s).
a) Phương trình vận tốc của chất điểm tại tời điểm t được xác định bởi công thức \(v\left( t \right) = \int {a\left( t \right)} dt\).
b) Tại thời điểm t = 7 (s), vận tốc của chất điểm là 6 (m/s).
c) Độ dịch chuyển của vật trong khoảng thời gian \(1 \le t \le 7\) là 18 m.
d) Trong 8 giây đầu tiên, thời điểm chất điểm xa nhất về phía bên phải là t = 7 (s).
Ứng dụng nguyên hàm để tìm công thức tính vận tốc và độ dịch chuyển. Ứng dụng đạo hàm để tìm giá trị lớn nhất.
a) Đúng. Phương trình vận tốc của chất điểm tại thời điểm t được xác định bởi công thức \(v\left( t \right) = \int {a\left( t \right)} dt.\)
b) Đúng. Ta có \(v\left( t \right) = \int {a\left( t \right)dt} = \int {\left( {2t - 7} \right)dt} = {t^2} - 7t + C\).
\(v\left( 0 \right) = 6 \Rightarrow C = 6 \Rightarrow v\left( t \right) = {t^2} - 7t + 6.\)
Vậy \(v\left( 7 \right) = {7^2} - 7.7 + 6 = 6\) (m/s).
c) Sai. Độ dịch chuyển của vật trong khoảng thời gian \(1 \le t \le 7\) là:
\(S = \int\limits_1^7 {v\left( t \right)} dt = \int\limits_1^7 {\left( {{t^2} - 7t + 6} \right)} dt = \left. {\left( {\frac{{{t^3}}}{3} - \frac{{7{t^2}}}{2} + 6t} \right)} \right|_1^7 = - 18.\)
d) Sai. Vị trí của chất điểm so với vị trí ban đầu tại thời điểm t là
\(s\left( t \right) = \int {v\left( t \right){\rm{d}}t} = \int {\left( {{t^2} - 7t + 6} \right){\rm{d}}t} = \frac{{{t^3}}}{3} - \frac{{7{t^2}}}{2} + 6t + C\)
Ta cần tìm giá trị lớn nhất của s(t) với \(t \in \left[ {0;\,8} \right]\).
Do s’(t) = v (t) nên \(s'\left( t \right) = 0 \Leftrightarrow v\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = 6\end{array} \right.\).
Lại có \(s\left( 0 \right) = C\), \(s\left( 1 \right) = \frac{{17}}{6} + C\), \(s\left( 6 \right) = - 18 + C\), \(s\left( 8 \right) = - \frac{{16}}{3} + C\).
Vậy giá trị lớn nhất của s(t) với \(t \in \left[ {0;\,8} \right]\) đạt được khi t = 1.
a) Tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 14\).
b) Tứ phân vị thứ ba của dãy số liệu là \({Q_3} = 11,5\).
c) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

d) Ước lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên ta được tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = 8,25\).
a) Tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 14\).
b) Tứ phân vị thứ ba của dãy số liệu là \({Q_3} = 11,5\).
c) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

d) Ước lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên ta được tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = 8,25\).
a, b) Sắp xếp mẫu số liệu gốc theo thứ tự từ nhỏ đến lớn rồi tìm tứ phân vị.
c, d) Ghép nhóm mẫu số liệu rồi ước lượng tứ phân vị.
Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
6; 8; 8; 10; 11; 11l 12; 13; 14; 14; 14; 15; 18. 21; 22; 23; 24; 25; 25.
a) Đúng. Tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = \frac{{14 + 14}}{2} = 14\).
b) Sai. Tứ phân vị thứ hai của dãy số liệu là: \({Q_3} = \frac{{21 + 22}}{2} = 21,5\).
c) Đúng. Ghép nhóm mẫu số liệu:

d) Sai. Vì số trận là số nguyên nên ta hiệu chỉnh lại bảng số liệu sau:

Gọi \({x_1};{x_2}; \ldots ;{x_{20}}\) lần lượt là số điểm ghi được ở mỗi trận đấu xếp theo thứ tự không giảm.
Do \({x_1}; \ldots ;{x_4} \in [5,5;10,5);{x_5}; \ldots ;{x_{12}} \in [10,5;15,5);{x_{13}},{x_{14}} \in [15,5;20,5);{x_{15}}; \ldots ;{x_{20}} \in [20,5;25,5)\) nên trung vị của mẫu số liệu \({x_1}; \ldots ;{x_{20}}\) là \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) \in [10,5;15,5)\).
Ta xác định được \(n = 20,{n_m} = 8,C = 4,{u_m} = 10,5;{u_{m + 1}} = 15,5\).
Suy ra tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}(15,5 - 10,5) = 14,25\).
Cho hình chóp S.ABCD có đáy là hình chữ nhật có cạnh AB = 2a, AD = a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm AB và CD.
a) \(SH \bot (ABCD)\).
b) Góc giữa SC và (ABCD) là góc \(\widehat {SHC}\).
c) Góc phẳng nhị diện [S,AB,C] bằng \({90^o}\).
d) Góc phẳng nhị diện [S,CD,A] bằng \({45^o}\).
a) \(SH \bot (ABCD)\).
b) Góc giữa SC và (ABCD) là góc \(\widehat {SHC}\).
c) Góc phẳng nhị diện [S,AB,C] bằng \({90^o}\).
d) Góc phẳng nhị diện [S,CD,A] bằng \({45^o}\).
Áp dụng điều kiện đường thẳng vuông góc với mặt phẳng, quy tắc xác định góc nhị diện.
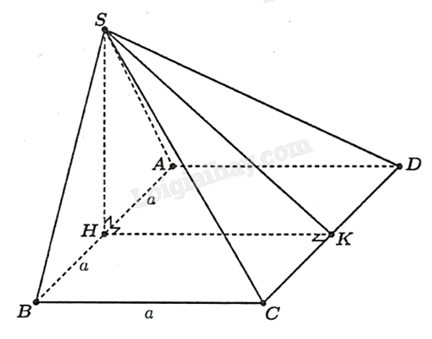
a) Đúng. Vì \(\left\{ \begin{array}{l}(SAB) \bot (ABCD)\\(SAB) \cap (ABCD) = AB\\SH \bot AB\,,\,SH \subset (SAB)\end{array} \right.\,\,\,\, \Rightarrow SH \bot (ABCD)\).
b) Sai. Hình chiếu của SC lên (ABCD) là HC nên góc \(\widehat {SCH}\) là góc giữa SC và (ABCD).
c) Đúng. Vì \((SAB) \bot (ABC)\) nên số đo của góc phẳng góc nhị diện [S,AB,C] bằng \({90^o}\).
d) Sai. Ta có: \(CD \bot HK\) (3).
Mặt khác \(SH \bot (ABCD)\) nên \(CD \bot SH\).
Suy ra \(CD \bot (SHK) \Rightarrow CD \bot SK\) (4).
Từ (3) và (4) suy ra \(\widehat {SKH}\) là góc phẳng nhị diện \([S,CD,A]\).
Tam giác \(SAB\) đều cạnh 2a nên đường cao \(SH = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).
Mà HK = BC = a (tính chất đường trung bình của hình chữ nhật).
Do đó \(\tan \widehat {SKH} = \frac{{SH}}{{HK}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SKH} = {60^o}\).
Cho hàm số \(y = {e^x}\left( {{x^2} - 3} \right)\), gọi \(M = \frac{a}{{{e^b}}}\) \(\left( {a \in \mathbb{N},b \in \mathbb{N}} \right)\) là giá trị lớn nhất của hàm số trên đoạn [-5;-2]. Tính giá trị của biểu thức P = a + b?
Đáp án:
Đáp án:
Ứng dụng đạo hàm để tìm giá trị lớn nhất.
Ta có: \(y' = {e^x}\left( {{x^2} - 3} \right) + {e^x}.2x = {e^x}\left( {{x^2} + 2{\rm{x}} - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3 \in \left[ { - 5; - 2} \right]\\x = 1 \notin \left[ { - 5; - 2} \right]\end{array} \right.\).
Ta có \(y\left( { - 5} \right) = \frac{{22}}{{{e^5}}};y\left( { - 3} \right) = \frac{6}{{{e^3}}};y\left( { - 2} \right) = \frac{1}{{{e^2}}}\).
Khi đó \(\mathop {\max }\limits_{\left[ { - 5; - 2} \right]} y = \frac{6}{{{e^3}}} \Rightarrow a = 6;b = 3 \Rightarrow a + b = 9\).
Cho hình lăng trụ tam giác ABC.A’B’C’ đáy là tam giác vuông cân có cạnh huyền \(AB = \sqrt 8 \). Khoảng cách giữa hai đường thẳng AB và B’C’ bằng 3. Tính thể tích khối chóp B.ACC’A’.

Đáp án:
Đáp án:
\(V = {V_{B.A'B'C'}} + {V_{B.ACC'A'}}\).
Vì ABC là tam giác vuông cân tại C nên \(A{C^2} + B{C^2} = A{B^2} \Leftrightarrow 2A{C^2} = 8 \Leftrightarrow AC = BC = 2\).
Diện tích tam giác ABC là \({S_{ABC}} = \frac{1}{2}.AC.BC = \frac{1}{2}.2.2 = 2\).
ABC.A’B’C’ là hình lăng trụ nên (ABC) // (A’B’C’), do đó khoảng cách từ AB đến B’C’ cũng là khoảng cách từ (ABC) đến (A’B’C’), hay chiều cao của lăng trụ bằng 3.
Thể tích lăng trụ là \(V = {S_{ABC}}.h = 2.3 = 6\).
Mà \(V = {V_{B.A'B'C'}} + {V_{B.ACC'A'}} \Leftrightarrow V = \frac{1}{3}V + {V_{B.ACC'A'}} \)
\(\Leftrightarrow {V_{B.ACC'A'}} = \frac{2}{3}V = \frac{2}{3}.6 = 4\).
Một căn phòng dạng hình hộp chữ nhật với chiều dài 8m, rộng 6m và cao 4m có hai chiếc quạt treo tường. Chiếc quạt A treo chính giữa bức tường 8m và cách trần 1m, chiếc quạt B treo chính giữa bức tường 6m và cách trần 1,5m. Hỏi khoảng cách giữa hai chiếc quạt AB cách nhau bao nhiêu m (làm tròn đến hàng phần nghìn)?

Đáp án:
Đáp án:
Tìm tọa độ hai chiếc quạt dựa vào hệ trục đó rồi tính khoảng cách.
Công thức tính khoảng cách: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
Ta có A(4;0;3) và điểm \(B\left( {0;3;\frac{5}{2}} \right)\).
Khoảng cách giữa hai chiếc quạt là:
\(AB = \sqrt {{{(0 - 4)}^2} + {{(3 - 0)}^2} + {{\left( {\frac{5}{2} - 3} \right)}^2}} = \frac{{\sqrt {101} }}{2} \approx 5,025\) (m).
Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc, xây dựng, thiết bị nội thất,... Một bồn rửa (lavabo) bằng sứ có hình dạng là một nửa khối tròn xoay khi elip quay quanh một trục (hình minh họa). Thông số kĩ thuật mặt trên của bồn rửa: dài \( \times \) rộng là \(660 \times 380{\rm{mm}},\) giả thiết bồn rửa có độ dày đồng đều \(\delta \) là \(20{\rm{mm}}\).

Thể tích chứa nước của bồn rửa bằng bao nhiêu decimet khối (làm tròn đến hàng phần trăm)?
Đáp án:
Đáp án:
Đưa về tính tích phân thể tích.
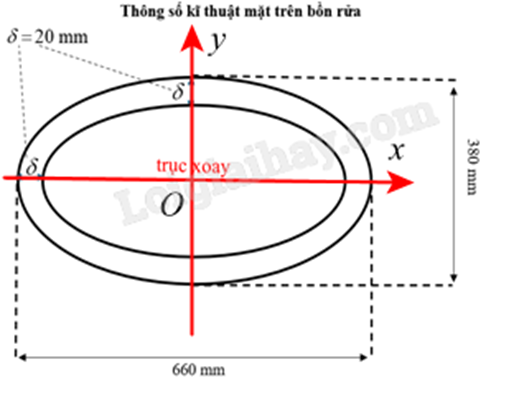
Elip bên trong có trục lớn bằng 660 – 20.2 = 620 và trục bé bằng 380 – 20.2 = 340 có phương trình:
\(\frac{{{x^2}}}{{{{310}^2}}} + \frac{{{y^2}}}{{{{170}^2}}} = 1 \Leftrightarrow {y_1}^2 = {170^2}.\left( {1 - \frac{{{x^2}}}{{{{310}^2}}}} \right)\).
Thể tích bồn chứa nước là:
\(V = \frac{1}{2}.\pi .\int\limits_{ - 310}^{310} {\left( {{{170}^2}.\left( {1 - \frac{{{x^2}}}{{{{310}^2}}}} \right)} \right)dx} {\rm{\;}} = 18763685m{m^3} = 18,76d{m^3}\).
Sự chuyển động của máy bay A được thể hiện trong không gian Oxyz như sau: Máy bay khởi hành từ B(0;0;2) chuyển động thẳng đều (tính theo phút) với vận tốc được biểu thị theo vecto \(\overrightarrow v (1;4;5)\). Sau khi khởi hành được 30 phút, máy bay ở vị trí M(x;y;z). Tính P = 3x + y + z.
Đáp án:
Đáp án:
Lập hàm số biểu diễn thể tích khối chóp theo ẩn x. Tìm x để thể tích khối chóp lớn nhất bằng cách ứng dụng đạo hàm, từ đó tính diện tích phần bạt bị cắt.
Ta có \(BM = \left| {\overrightarrow v } \right|.t \Rightarrow \overrightarrow {BM} = \overrightarrow v .30 \Leftrightarrow (x;y;z - 2) = (1.30;4.30;5.30) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = 30}\\{y = 120}\\{z - 2 = 150}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 30}\\{y = 120}\\{z = 152}\end{array}} \right.} \right.\).
Vậy P = 3.30 + 120 + 152 = 362.
Áo sơ mi G9 trước khi xuất khẩu sang Mỹ phải qua 2 lần kiểm tra, nếu cả hai lần đều đạt thì chiếc áo đó mới đủ tiêu chuẩn xuất khẩu. Biết rằng bình quân 95% sản phẩm làm ra qua được lần kiểm tra thứ nhất, và 92% sản phẩm qua được lần kiểm tra đầu sẽ tiếp tục qua được lần kiểm tra thứ hai. Xác suất để 1 chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu là \(\frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính a + b.
Đáp án:
Đáp án:
Áp dụng công thức nhân xác suất \(P(A \cap B) = P(B|A).P(A)\).
Gọi A là biến cố “qua được lần kiểm tra đầu tiên” \( \Rightarrow P\left( A \right) = 0,95\).
Gọi B là biến cố “qua được lần kiểm tra thứ 2” \( \Rightarrow P\left( {B|A} \right) = 0,92\).
Chiếc áo sơ mi đủ tiêu chuẩn xuất khẩu phải thỏa mãn 2 điều kiện A và B, do đó ta cần tính \(P\left( {A \cap B} \right)\).
Ta có \(P\left( {B|A} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}} \Rightarrow P\left( {A \cap B} \right) = P\left( {B|A} \right).P\left( A \right) = 0,95.0,92 = \frac{{437}}{{500}}.\)
Suy ra a + b = 437 + 500 = 937.
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Các bài khác cùng chuyên mục
- Đề thi thử THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
- Đề thi THPT môn Toán năm 2025 (Mã 123) có lời giải
- Đề tham khảo thi THPT môn Toán - Đề số 10 (hay, chi tiết)
- Đề khảo sát chất lượng Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội
- Đề thi thử THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
- Đề thi THPT môn Toán năm 2025 (Mã 123) có lời giải
- Đề tham khảo thi THPT môn Toán - Đề số 10 (hay, chi tiết)
- Đề khảo sát chất lượng Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội









