Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Vĩnh Phúc
I. Phần trắc nghiệm
Đề bài
Chọn ngẫu nhiên 3 bạn từ một tổ có 10 học sinh (gồm 6 bạn nữ và 4 bạn nam), xác suất chọn được 3
bạn nam là
-
A.
\(\frac{1}{{30}}\)
-
B.
\(\frac{3}{{10}}\)
-
C.
\(\frac{1}{5}\)
-
D.
\(\frac{1}{6}\)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và \(SA = a\sqrt 3 \). Thể tích khối chóp S.ABC bằng
-
A.
\(\frac{{{a^3}}}{8}\)
-
B.
\(\frac{{{a^3}}}{2}\)
-
C.
\(\frac{{3{a^3}}}{4}\)
-
D.
\(\frac{{{a^3}}}{4}\)
Tập xác định của hàm số \(y = {\log _3}(x - 5)\) là
-
A.
\(( - \infty ; + \infty )\)
-
B.
\((5; + \infty )\)
-
C.
\([5; + \infty )\)
-
D.
\(( - \infty ;5)\)
Cho mẫu số liệu ghép nhóm về số tiền mà 60 khách hàng mua sách ở một cửa hàng trong một ngày như sau:

Tứ phân vị thứ nhất của mẫu là
-
A.
\({Q_1} = 25\)
-
B.
\({Q_1} = 60\)
-
C.
\({Q_1} = 60,8\)
-
D.
\({Q_1} = 65\)
Cho hình hộp ABCD.A’B’C’D’. Mệnh đề nào dưới đây là mệnh đề đúng?
-
A.
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} \)
-
B.
\(\overrightarrow {AB'} = \overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} \)
-
C.
\(\overrightarrow {A'D} = \overrightarrow {A'B'} + \overrightarrow {A'C} \)
-
D.
\(\overrightarrow {AD'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AC'} \)
Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x - 2024}}{{x + 1}}\) là
-
A.
\(y = - 1\)
-
B.
\(x = 2\)
-
C.
\(y = \frac{1}{2}\)
-
D.
\(y = 2\)
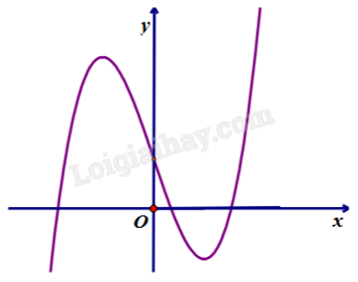
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ sau:
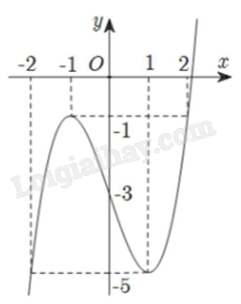
Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số đã cho trên đoạn [-2;2] bằng
-
A.
0
-
B.
-1
-
C.
-5
-
D.
-6
Trong không gian Oxyz, cho \(\overrightarrow a = (2;1;3)\) và \(\overrightarrow b = ( - 1;2;1)\). Tọa độ của vecto \(\overrightarrow a + \overrightarrow b \) là
-
A.
\(\overrightarrow a + \overrightarrow b = (3; - 1;2)\)
-
B.
\(\overrightarrow a + \overrightarrow b = ( - 1;3;4)\)
-
C.
\(\overrightarrow a + \overrightarrow b = (1;3;4)\)
-
D.
\(\overrightarrow a + \overrightarrow b = (2; - 1;2)\)
Giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - x + 3}}{{x + 2}}\) bằng
-
A.
\( - 1\)
-
B.
\(1\)
-
C.
\(\frac{{ - 3}}{2}\)
-
D.
\( - 3\)
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) có đạo hàm \(f'(x) = (x + 1)(x - 2)\), \(\forall x \in \mathbb{R}\). Hàm số đã cho nghịch biến trên khoảng nào sau đây?
-
A.
\((2; + \infty )\)
-
B.
\(( - \infty ;2)\)
-
C.
\(( - 1;2)\)
-
D.
\(( - 1; + \infty )\)
Cho hàm số y = f(x) liên tục trên và có bảng xét dấu của f’(x) như hình dưới:
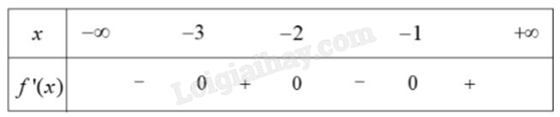
Hàm số y = f(x) có bao nhiêu điểm cực trị?
-
A.
1
-
B.
2
-
C.
4
-
D.
3
-
A.
\(f(x) = {x^3} + 3x + 1\)
-
B.
\(f(x) = {x^3} - 3x - 1\)
-
C.
\(f(x) = {x^3} - 3x + 1\)
-
D.
\(f(x) = - {x^3} - 3x + 1\)
Cho hàm số \(f(x) = 5x - {\log _3}(x + 1)\).
a) Hàm số f(x) nghịch biến trên khoảng (1;0) .
b) Hàm số f(x) có một điểm cực đại.
c) Đạo hàm của hàm số f(x) là \(f'(x) = 5 - \frac{1}{{(x + 1)\ln 3}}\), \(\forall x \in ( - 1; + \infty )\).
d) Giá trị của hàm số f(x) tại điểm x = 2 là f(2) = 9.
Hệ thống cáp treo gồm hai trụ lớn và một đường cáp nối thẳng giữa hai trụ đó (coi như độ cong không đáng kể), được đặt trong không gian với hệ tọa độ Oxyz. Một cabin cáp treo xuất phát từ điểm O(0;0;0) thuộc trụ thứ nhất và chuyển động thẳng đều theo đường cáp đến điểm A(896;2025;189) thuộc trụ thứ hai với tốc độ là 7,4 (m/s) (đơn vị trên mỗi trục là mét).
a) Điểm chính giữa của đường cáp có tọa độ là (448;1210,5;94,5).
b) Có một khu vui chơi phía dưới cáp treo nằm trong mặt phẳng (Oxy) với điểm trung tâm có tọa độ
(750,5;1497,25;0). Biết rằng từ trong cabin cáp treo có thể ngắm nhìn toàn cảnh khu vui chơi rõ nhất tại vị trí điểm \(M({x_0};{y_0};{z_0})\) cách trung tâm khu vui chơi một khoảng ngắn nhất. Khi đó ta có \({x_0} + {y_0} + {z_0} \approx 2332,5\) (kết quả làm tròn đến hàng phần mười).
c) Trên đường cáp có điểm B với hoành độ \({x_B} = 672\), khi đó thời gian để cabin đi từ điểm B đến điểm A xấp xỉ là 70 giây (kết quả làm tròn đến hàng đơn vị).
d) Độ dài đường cáp xấp xỉ bằng 2220 m (kết quả làm tròn đến hàng đơn vị).
Thông kê kết quả điểm trung bình học kì 1 của hai nhóm học sinh thuộc hai trường X và Y ta lập được bảng sau:

a) Nếu so sánh theo độ lệch chuẩn của hai mẫu số liệu thì nhóm học sinh trường X có điểm trung bình đều hơn nhóm học sinh trường Y.
b) Khoảng tứ phân vị của mẫu số liệu trường Y (làm tròn đến hàng phần trăm) là \({\Delta _Q} = 1,73\).
c) Cỡ của mẫu mẫu số liệu trường X là 18, cỡ của mẫu số liệu trường Y là 12.
d) Nếu so sánh độ khoảng tứ phân vị của hai mẫu số liệu thì nhóm học sinh trường Y có điểm trung bình đều hơn nhóm học sinh trường X.
Một cửa hàng bán bưởi da xanh Bến Tre với giá bán là 50000 đồng/1 quả. Giá nhập vào là 30000 đồng/1 quả. Với giá bán này của hàng bán được 100 quả/1 ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm 1000 đồng/1 quả thì số bưởi da xanh bán được sẽ tăng thêm là 10 quả.
a) Nếu giữ nguyên giá ban đầu, lợi nhuận theo ngày của cửa hàng là 2200000 đồng.
b) Lợi nhuận tối đa theo ngày của cửa hàng là 2200000 đồng.
c) Nếu giá bán là 44000 đồng/1 quả, khi đó cửa hàng bán được 150 quả/1 ngày.
d) Nếu giá bán là 40000 đồng/1 quả, khi đó lợi nhuận theo ngày của cửa hàng là 2000000 đồng.
Một xí nghiệp may áo vest và quần âu để chuẩn bị cho dịp cuối năm. Biết may 1 áo vest hết 2m vải và cần 20 giờ; may 1 quần âu hết 1,5m vải và cần 5 giờ. Xí nghiệp được giao sử dụng không quá 900m vải và 60 giờ công không vượt quá 6000 giờ. Theo khảo sát thị trường, số lượng quần âu bán ra không nhỏ hơn số lượng áo vest bán ra và số lượng quần áo bán ra không vượt quá 2 lần số lượng áo vest bán ra. Khi xuất ra thị trường, 1 chiếc áo vest là 350 nghìn đồng, 1 chiếc quần âu là 100 nghìn đồng. Gọi x, y lần lượt là số áo vest và quần âu xí nghiệp có sẽ sản xuất. Tính giá trị của biểu thức T = 2x + 3y.
Đáp án:
Trong không gian Oxyz, cho tam giác ABC biết A(1;-1;2), B(-2;0;3), C(0;1;-2). Gọi M(a;b;c) là điểm thuộc mặt phẳng (Oxy) sao cho biểu thức đạt giá trị nhỏ nhất. Tính giá trị của biểu thức T = 12a + 12b + c.
Đáp án:
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 1 và thể tích bằng \(\frac{2}{3}\). Gọi G là trọng tâm của tam giác SCD. Trên các cạnh AB, SD, lần lượt lấy các điểm E, F sao cho EF song song BG. Khoảng cách giữa hai đường thẳng DG và EF bằng \(\frac{m}{n}\) với m, n nguyên dương \(\frac{m}{n}\) là phân số tối giản. Tính giá trị của biểu thức T = 2m – n.
Đáp án:
Người ta muốn xây một bể chứa nước lớn dạng một khối hộp chữ nhật không nắp (xây bốn mặt xung quanh và mặt đáy) có thể tích lớn hơn 432 \({m^3}\) nước. Đây là bể hình chữ nhật có chiều dài gấp đôi chiều rộng, tính chi phí xây bể là 400.000 đồng/\({m^2}\) (tính trên diện tích mặt trong bể). Hỏi chi phí thấp nhất để xây bể là bao nhiêu triệu đồng (kết quả làm tròn đến hàng đơn vị)?
Đáp án:
Một công ty kinh doanh dịch vụ nhận thấy rằng: Nếu áp dụng mức giá 3 triệu đồng/người/ngày thì mỗi tháng có 160 khách đến nghỉ và mỗi khách sẽ nghỉ 10 ngày. Nếu có tăng giá thêm 500 nghìn đồng/người/ngày thì mỗi tháng sẽ có khách đến nghỉ sẽ giảm 4 người và thời gian lưu trú của mỗi người khách cũng giảm đi 2 ngày. Ngược lại, nếu công ty giữ nguyên mức giá 500 nghìn đồng/người/ngày thì hàng tháng số khách đến nghỉ sẽ tăng thêm 4 người và thời gian lưu trú của một khách cũng tăng thêm 2 ngày. Hỏi công ty cần áp dụng mức giá bao nhiêu triệu đồng/người/ngày để lợi nhuận tháng thu được là lớn nhất, biết tổng chi phí công ty phải chi cho một ngày lưu trú của mỗi khách là 2 triệu đồng và Sở du lịch không cho công ty thu vượt quá 10 triệu đồng/người/ngày?
Đáp án:
Cho \(\cot \alpha = \frac{1}{3}\). Biết giá trị của biểu thức \(\frac{{3\sin \alpha + 4\cos \alpha }}{{2\sin \alpha - 5\cos \alpha }}\) có dạng \(\frac{a}{b}\) (với \(a,b \in \mathbb{N}\); \(b \ne 0\), \(\frac{a}{b}\) là phân số tối giản). Tính giá trị của biểu thức T = 100a + b.
Đáp án:
Lời giải và đáp án
Chọn ngẫu nhiên 3 bạn từ một tổ có 10 học sinh (gồm 6 bạn nữ và 4 bạn nam), xác suất chọn được 3
bạn nam là
-
A.
\(\frac{1}{{30}}\)
-
B.
\(\frac{3}{{10}}\)
-
C.
\(\frac{1}{5}\)
-
D.
\(\frac{1}{6}\)
Đáp án : A
Sử dụng phương pháp tổ hợp.
Xác suất để chọn được 3 bạn nam là \(\frac{{C_4^3}}{{C_{10}^3}} = \frac{1}{{30}}\).
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy và \(SA = a\sqrt 3 \). Thể tích khối chóp S.ABC bằng
-
A.
\(\frac{{{a^3}}}{8}\)
-
B.
\(\frac{{{a^3}}}{2}\)
-
C.
\(\frac{{3{a^3}}}{4}\)
-
D.
\(\frac{{{a^3}}}{4}\)
Đáp án : D
Sử dụng công thức tính thể tích khối chóp \({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.h\).
Diện tích tam giác đều cạnh a là \({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\).
\({V_{S.ABC}} = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.a\sqrt 3 = \frac{{{a^3}}}{4}\).
Tập xác định của hàm số \(y = {\log _3}(x - 5)\) là
-
A.
\(( - \infty ; + \infty )\)
-
B.
\((5; + \infty )\)
-
C.
\([5; + \infty )\)
-
D.
\(( - \infty ;5)\)
Đáp án : B
Tập xác định của hàm số \(y = {\log _a}x\) là \((x; + \infty )\).
Điều kiện: x – 5 > 0 hay x > 5 nên tập xác định của hàm số \(y = {\log _3}(x - 5)\) là \((5; + \infty )\).
Cho mẫu số liệu ghép nhóm về số tiền mà 60 khách hàng mua sách ở một cửa hàng trong một ngày như sau:

Tứ phân vị thứ nhất của mẫu là
-
A.
\({Q_1} = 25\)
-
B.
\({Q_1} = 60\)
-
C.
\({Q_1} = 60,8\)
-
D.
\({Q_1} = 65\)
Đáp án : C
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.({u_{m + 1}} - {u_m})\).
Cỡ mẫu: n = 5 + 8 + 25 + 20 + 2 = 60.
\({Q_1} = 60 + \frac{{\frac{{60}}{4} - (5 + 8)}}{{25}}.(70 - 60) = 60,8\).
Cho hình hộp ABCD.A’B’C’D’. Mệnh đề nào dưới đây là mệnh đề đúng?
-
A.
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} \)
-
B.
\(\overrightarrow {AB'} = \overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} \)
-
C.
\(\overrightarrow {A'D} = \overrightarrow {A'B'} + \overrightarrow {A'C} \)
-
D.
\(\overrightarrow {AD'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AC'} \)
Đáp án : A
Áp dụng quy tắc hình hộp.
Theo quy tắc hình hộp, ta có \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} \).
Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x - 2024}}{{x + 1}}\) là
-
A.
\(y = - 1\)
-
B.
\(x = 2\)
-
C.
\(y = \frac{1}{2}\)
-
D.
\(y = 2\)
Đáp án : D
Đồ thị hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đường tiệm cận ngang là \(y = \frac{a}{c}\).
Đường tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x - 2024}}{{x + 1}}\) là \(y = 2\).
Cho hàm số y = f(x) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ sau:

Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số đã cho trên đoạn [-2;2] bằng
-
A.
0
-
B.
-1
-
C.
-5
-
D.
-6
Đáp án : D
Quan sát đồ thị và nhận xét.
Trên đoạn [-2;2], hàm số có giá trị lớn nhất là -1, giá trị nhỏ nhất là -5. Tổng của chúng là -6.
Trong không gian Oxyz, cho \(\overrightarrow a = (2;1;3)\) và \(\overrightarrow b = ( - 1;2;1)\). Tọa độ của vecto \(\overrightarrow a + \overrightarrow b \) là
-
A.
\(\overrightarrow a + \overrightarrow b = (3; - 1;2)\)
-
B.
\(\overrightarrow a + \overrightarrow b = ( - 1;3;4)\)
-
C.
\(\overrightarrow a + \overrightarrow b = (1;3;4)\)
-
D.
\(\overrightarrow a + \overrightarrow b = (2; - 1;2)\)
Đáp án : C
Áp dụng biểu thức tọa độ phép cộng hai vecto.
\(\overrightarrow a + \overrightarrow b = (2 - 1;1 + 2;3 + 1) = (1;3;4)\).
Giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - x + 3}}{{x + 2}}\) bằng
-
A.
\( - 1\)
-
B.
\(1\)
-
C.
\(\frac{{ - 3}}{2}\)
-
D.
\( - 3\)
Đáp án : A
Áp dụng quy tắc tính giới hạn đặc biệt: \(\mathop {\lim }\limits_{x \to \infty } \frac{1}{x} = 0\).
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{ - x + 3}}{{x + 2}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{x\left( { - 1 + \frac{3}{x}} \right)}}{{x\left( {1 + \frac{2}{x}} \right)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{ - 1 + \frac{3}{x}}}{{1 + \frac{2}{x}}} = \frac{{ - 1 + 0}}{{1 + 0}} = - 1\).
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) có đạo hàm \(f'(x) = (x + 1)(x - 2)\), \(\forall x \in \mathbb{R}\). Hàm số đã cho nghịch biến trên khoảng nào sau đây?
-
A.
\((2; + \infty )\)
-
B.
\(( - \infty ;2)\)
-
C.
\(( - 1;2)\)
-
D.
\(( - 1; + \infty )\)
Đáp án : C
Lập bảng xét dấu.

Vậy đạo hàm f’(x) nghịch biến trên khoảng (-1;2).
Cho hàm số y = f(x) liên tục trên và có bảng xét dấu của f’(x) như hình dưới:

Hàm số y = f(x) có bao nhiêu điểm cực trị?
-
A.
1
-
B.
2
-
C.
4
-
D.
3
Đáp án : D
Hàm số đạt cực trị tại điểm thỏa mãn hai điều kiện:
- Đạo hàm của hàm số bằng 0 hoặc tại đó không tồn tại đạo hàm.
- Đạo hàm của hàm số đổi dấu.
Quan sát bảng xét dấu thấy f(x) có ba điểm cực trị x = -3; x = -2; x = -1.
-
A.
\(f(x) = {x^3} + 3x + 1\)
-
B.
\(f(x) = {x^3} - 3x - 1\)
-
C.
\(f(x) = {x^3} - 3x + 1\)
-
D.
\(f(x) = - {x^3} - 3x + 1\)
Đáp án : C
Quan sát đồ thị và nhận xét. Sử dụng phương pháp loại trừ.
Hàm số có dạng \(y = f(x) = a{x^3} + bx + c\).
Vì \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \) nên a > 0. Loại D.
Đồ thị cắt trục tung tại điểm có tung độ dương nên c > 0. Loại B.
Xét đáp án A: \(f'(x) = 3{x^2} + 3 = 0 \Leftrightarrow {x^2} = - 1\) (vô lí) nên hàm số \(f(x) = {x^3} + 3x + 1\) không có cực trị. Loại A.
Cho hàm số \(f(x) = 5x - {\log _3}(x + 1)\).
a) Hàm số f(x) nghịch biến trên khoảng (1;0) .
b) Hàm số f(x) có một điểm cực đại.
c) Đạo hàm của hàm số f(x) là \(f'(x) = 5 - \frac{1}{{(x + 1)\ln 3}}\), \(\forall x \in ( - 1; + \infty )\).
d) Giá trị của hàm số f(x) tại điểm x = 2 là f(2) = 9.
a) Hàm số f(x) nghịch biến trên khoảng (1;0) .
b) Hàm số f(x) có một điểm cực đại.
c) Đạo hàm của hàm số f(x) là \(f'(x) = 5 - \frac{1}{{(x + 1)\ln 3}}\), \(\forall x \in ( - 1; + \infty )\).
d) Giá trị của hàm số f(x) tại điểm x = 2 là f(2) = 9.
Tìm tập xác định của hàm số, tính đạo hàm, lập bảng biến thiên và kết luận.
Tập xác định: \(D = ( - 1; + \infty )\).
\(f'(x) = 5 - \frac{{(x + 1)'}}{{(x + 1)\ln 3}} = 5 - \frac{1}{{(x + 1)\ln 3}}\).
\(f'(x) = 0 \Leftrightarrow 5 = \frac{1}{{(x + 1)\ln 3}} \Leftrightarrow x = \frac{1}{{5\ln 3}} - 1 \approx - 0,8\).
Bảng biến thiên:

a) Sai. Hàm số nghịch biến trên \(\left( { - 1;\frac{1}{{5\ln 3}} - 1} \right)\) và đồng biến trên \(\left( {\frac{1}{{5\ln 3}} - 1;0} \right)\).
b) Sai. Hàm số không có điểm cực đại.
c) Đúng. \(f'(x) = 5 - \frac{{(x + 1)'}}{{(x + 1)\ln 3}} = 5 - \frac{1}{{(x + 1)\ln 3}}\).
d) Đúng. \(f(2) = 5.2 - {\log _3}(2 + 1) = 10 - 1 = 9\).
Hệ thống cáp treo gồm hai trụ lớn và một đường cáp nối thẳng giữa hai trụ đó (coi như độ cong không đáng kể), được đặt trong không gian với hệ tọa độ Oxyz. Một cabin cáp treo xuất phát từ điểm O(0;0;0) thuộc trụ thứ nhất và chuyển động thẳng đều theo đường cáp đến điểm A(896;2025;189) thuộc trụ thứ hai với tốc độ là 7,4 (m/s) (đơn vị trên mỗi trục là mét).
a) Điểm chính giữa của đường cáp có tọa độ là (448;1210,5;94,5).
b) Có một khu vui chơi phía dưới cáp treo nằm trong mặt phẳng (Oxy) với điểm trung tâm có tọa độ
(750,5;1497,25;0). Biết rằng từ trong cabin cáp treo có thể ngắm nhìn toàn cảnh khu vui chơi rõ nhất tại vị trí điểm \(M({x_0};{y_0};{z_0})\) cách trung tâm khu vui chơi một khoảng ngắn nhất. Khi đó ta có \({x_0} + {y_0} + {z_0} \approx 2332,5\) (kết quả làm tròn đến hàng phần mười).
c) Trên đường cáp có điểm B với hoành độ \({x_B} = 672\), khi đó thời gian để cabin đi từ điểm B đến điểm A xấp xỉ là 70 giây (kết quả làm tròn đến hàng đơn vị).
d) Độ dài đường cáp xấp xỉ bằng 2220 m (kết quả làm tròn đến hàng đơn vị).
a) Điểm chính giữa của đường cáp có tọa độ là (448;1210,5;94,5).
b) Có một khu vui chơi phía dưới cáp treo nằm trong mặt phẳng (Oxy) với điểm trung tâm có tọa độ
(750,5;1497,25;0). Biết rằng từ trong cabin cáp treo có thể ngắm nhìn toàn cảnh khu vui chơi rõ nhất tại vị trí điểm \(M({x_0};{y_0};{z_0})\) cách trung tâm khu vui chơi một khoảng ngắn nhất. Khi đó ta có \({x_0} + {y_0} + {z_0} \approx 2332,5\) (kết quả làm tròn đến hàng phần mười).
c) Trên đường cáp có điểm B với hoành độ \({x_B} = 672\), khi đó thời gian để cabin đi từ điểm B đến điểm A xấp xỉ là 70 giây (kết quả làm tròn đến hàng đơn vị).
d) Độ dài đường cáp xấp xỉ bằng 2220 m (kết quả làm tròn đến hàng đơn vị).
a) Áp dụng công thức tính tọa độ trung điểm.
b) Ứng dụng điều kiện của hai vecto cùng phương và tìm giá trị nhỏ nhất bằng cách ứng dụng đạo hàm.
c) Ứng dụng điều kiện của hai vecto cùng phương, tìm độ dài quãng đường, từ đó tính được thời gian.
d) Áp dụng công thức tính khoảng cách giữa hai điểm.
a) Đúng. Gọi điểm chính giữa đường cáp là I, khi đó I là trung điểm của OA.
Ta có \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_O} + {x_A}}}{2} = \frac{{0 + 896}}{2} = 448\\{y_I} = \frac{{{y_O} + {y_A}}}{2} = \frac{{0 + 2025}}{2} = 1012,5\\{z_I} = \frac{{{z_O} + {z_A}}}{2} = \frac{{0 + 189}}{2} = 94,5\end{array} \right.\), suy ra I(448; 1012,5; 94,5).
b) Đúng. Gọi vị trí khu vui chơi là B(750,5; 1497,25; 0).
\(\overrightarrow {OA} = (896;2025;189)\).
Vì \(M({x_0};{y_0};{z_0})\) thuộc đường cáp nên \(\overrightarrow {OM} = k\overrightarrow {OA} \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 896k\\{y_0} = 2025k\\{z_0} = 189k\end{array} \right.\) \((k \in \mathbb{Z})\).
\(\overrightarrow {BM} = ({x_0} - 750,5;{y_0} - 1497,25;{z_0})\).
\(\left| {\overrightarrow {BM} } \right| = \sqrt {{{({x_0} - 750,5)}^2} + {{({y_0} - 1497,25)}^2} + {z_0}^2} \)
\( = \sqrt {{{(896k - 750,5)}^2} + {{(2025k - 1497,25)}^2} + {{(189k)}^2}} \)
\(B{M^2} = 4939162{k^2} + 7408758,5k + 280007,813\).
Cabin cách khu vui chơi một khoảng ngắn nhất khi BM ngắn nhất, hay \(B{M^2}\) ngắn nhất.
Cần tìm k để \(B{M^2}\) ngắn nhất. Bài toán trở thành tìm giá trị nhỏ nhất của hàm số \(f(k) = 4939162{k^2} + 7408758,5k + 280007,813\).
\(f'(k) = 9878324k + 7408758,5 = 0 \Leftrightarrow k \approx 0,75\).
Vì f(k) là hàm số bậc hai có đồ thị có bề lõm hướng lên trên nên giá trị nhỏ nhất của f(k) là giá trị tại điểm cực trị của hàm số f(k), tức \(k \approx 0,75\).
Vậy \({x_0} + {y_0} + {z_0} = 896.0,75 + 2025.0,75 + 189.0,75 \approx 2332,5\).
c) Sai. Điểm B thuộc đường cáp nên \(\left\{ \begin{array}{l}{x_B} = 896k' = 672\\{y_B} = 2025k'\\{z_B} = 189k'\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k' = 0,75\\{y_B} = 1518,75\\{z_B} = 141,75\end{array} \right.\).
Vậy B(672; 1518,75; 141,75).
\(AB = \sqrt {{{(672 - 896)}^2} + {{(1518,75 - 2025)}^2} + {{(141,75 - 189)}^2}} \approx 555,6\) (m).
Thời gian để đi từ B đến A là \(\frac{{AB}}{v} = \frac{{555,6}}{{7,4}} \approx 75\) (giây).
d) Sai. Độ dài đường cáp là \(OA = \sqrt {{{896}^2} + {{2025}^2} + {{189}^2}} \approx 2222\) (m).
Thông kê kết quả điểm trung bình học kì 1 của hai nhóm học sinh thuộc hai trường X và Y ta lập được bảng sau:

a) Nếu so sánh theo độ lệch chuẩn của hai mẫu số liệu thì nhóm học sinh trường X có điểm trung bình đều hơn nhóm học sinh trường Y.
b) Khoảng tứ phân vị của mẫu số liệu trường Y (làm tròn đến hàng phần trăm) là \({\Delta _Q} = 1,73\).
c) Cỡ của mẫu mẫu số liệu trường X là 18, cỡ của mẫu số liệu trường Y là 12.
d) Nếu so sánh độ khoảng tứ phân vị của hai mẫu số liệu thì nhóm học sinh trường Y có điểm trung bình đều hơn nhóm học sinh trường X.
a) Nếu so sánh theo độ lệch chuẩn của hai mẫu số liệu thì nhóm học sinh trường X có điểm trung bình đều hơn nhóm học sinh trường Y.
b) Khoảng tứ phân vị của mẫu số liệu trường Y (làm tròn đến hàng phần trăm) là \({\Delta _Q} = 1,73\).
c) Cỡ của mẫu mẫu số liệu trường X là 18, cỡ của mẫu số liệu trường Y là 12.
d) Nếu so sánh độ khoảng tứ phân vị của hai mẫu số liệu thì nhóm học sinh trường Y có điểm trung bình đều hơn nhóm học sinh trường X.
Áp dụng các công thức tính cỡ mẫu, độ lệch chuẩn, khoảng tứ phân vị rồi nhận xét.
a) Sai. \(\overline {{x_X}} = \frac{{5,5.4 + 6,5.5 + 7,5.3 + 8,5.4 + 9,5.2}}{{4 + 5 + 3 + 4 + 2}} = \frac{{65}}{9}\).
\(\overline {{x_Y}} = \frac{{5,5.2 + 6,5.5 + 7,5.4 + 8,5.3 + 9,5.1}}{{2 + 5 + 4 + 3 + 1}} = \frac{{217}}{{30}}\).
\(\sqrt {{s_X}^2} = \sqrt {\frac{1}{{18}}.\left[ {4.{{\left( {5,5 - \frac{{65}}{9}} \right)}^2} + 5.{{\left( {6,5 - \frac{{65}}{9}} \right)}^2} + 3.{{\left( {7,5 - \frac{{65}}{9}} \right)}^2} + 4.{{\left( {8,5 - \frac{{65}}{9}} \right)}^2} + 2.{{\left( {9,5 - \frac{{65}}{9}} \right)}^2}} \right]} = \sqrt {\frac{{569}}{{324}}} \).
\(\sqrt {{s_Y}^2} = \sqrt {\frac{1}{{15}}.\left[ {2.{{\left( {5,5 - \frac{{217}}{{30}}} \right)}^2} + 5.{{\left( {6,5 - \frac{{217}}{{30}}} \right)}^2} + 4.{{\left( {7,5 - \frac{{217}}{{30}}} \right)}^2} + 3.{{\left( {8,5 - \frac{{217}}{{30}}} \right)}^2} + 1.{{\left( {9,5 - \frac{{217}}{{30}}} \right)}^2}} \right]} = \sqrt {\frac{{284}}{{225}}} \).
Vì \(\sqrt {{s_Y}^2} < \sqrt {{s_X}^2} \) nên nhóm học sinh trường Y có điểm trung bình đều hơn nhóm học sinh trường X.
b) Đúng. Khoảng tứ phân vị trường Y là
\({\Delta _{{Q_Y}}} = {Q_3} - {Q_1} = 8 + \frac{{\frac{{15.3}}{4} - (2 + 5 + 4)}}{3}.(9 - 8) - 6 - \frac{{\frac{{15}}{4} - 2}}{5}.(7 - 6) \approx 1,73\).
c) Sai. Cỡ mẫu số liệu trường X là \({n_X} = 4 + 5 + 3 + 4 + 2 = 18\).
Cỡ mẫu số liệu trường Y là \({n_Y} = 2 + 5 + 4 + 3 + 1 = 15\).
d) Đúng. \({\Delta _{{Q_X}}} = {Q_3} - {Q_1} = 8 + \frac{{\frac{{18.3}}{4} - (4 + 5 + 3)}}{4}.(9 - 8) - 6 - \frac{{\frac{{18}}{4} - 4}}{5}.(7 - 6) = 2,275\).
Vì \({\Delta _{{Q_Y}}} < {\Delta _{{Q_X}}}\) nên nhóm học sinh trường Y có điểm trung bình đều hơn nhóm học sinh trường X.
Một cửa hàng bán bưởi da xanh Bến Tre với giá bán là 50000 đồng/1 quả. Giá nhập vào là 30000 đồng/1 quả. Với giá bán này của hàng bán được 100 quả/1 ngày. Cửa hàng dự định giảm giá bán, ước tính cứ giảm 1000 đồng/1 quả thì số bưởi da xanh bán được sẽ tăng thêm là 10 quả.
a) Nếu giữ nguyên giá ban đầu, lợi nhuận theo ngày của cửa hàng là 2200000 đồng.
b) Lợi nhuận tối đa theo ngày của cửa hàng là 2200000 đồng.
c) Nếu giá bán là 44000 đồng/1 quả, khi đó cửa hàng bán được 150 quả/1 ngày.
d) Nếu giá bán là 40000 đồng/1 quả, khi đó lợi nhuận theo ngày của cửa hàng là 2000000 đồng.
a) Nếu giữ nguyên giá ban đầu, lợi nhuận theo ngày của cửa hàng là 2200000 đồng.
b) Lợi nhuận tối đa theo ngày của cửa hàng là 2200000 đồng.
c) Nếu giá bán là 44000 đồng/1 quả, khi đó cửa hàng bán được 150 quả/1 ngày.
d) Nếu giá bán là 40000 đồng/1 quả, khi đó lợi nhuận theo ngày của cửa hàng là 2000000 đồng.
Đặt ẩn là giá bán thực tế của mỗi quả bưởi. Lập hàm số biểu diễn lợi nhuận của cửa hàng theo x, từ đó tính các giá trị theo yêu cầu đề bài.
a) Đúng. Giữ nguyên giá ban đầu, lợi nhuận theo ngày của của hàng là \((50000 - 30000).100 = 2000000\) (đồng).
b) Sai. Gọi x là giá bán thực tế của mỗi quả bưởi \((30000 \le x \le 50000)\).
Theo giả thiết, số quả bán được thêm mỗi ngày khi giảm giá còn x (đồng) là \(\frac{{50000 - x}}{{1000}}.10 = \frac{{50000 - x}}{{100}}\) (quả).
Vậy tổng số bưởi bán được khi bán với giá x (đồng) là \(100 + \frac{{50000 - x}}{{100}}\) (quả).
Lợi nhuận thu được khi đó là \(f(x) = \left( {100 + \frac{{50000 - x}}{{100}}} \right).\left( {x - 30000} \right) = - \frac{{{x^2}}}{{100}} + 900x - 18000000\) (đồng).
\(f'(x) = - \frac{x}{{50}} + 900 = 0 \Leftrightarrow x = 45000\) (đồng).
Có \(f(30000) = 0\); \(f(45000) = 2250000\); \(f(50000) = 2000000\).
Vậy lợi nhuận tối đa theo ngày là 2250000 đồng khi bán mỗi quả bưởi với giá 45000 đồng.
c) Sai. Số quả bưởi cửa hàng bán được trong ngày khi bán với giá 44000 đồng/quả là \(100 + \frac{{50000 - 44000}}{{100}} = 160\) (quả).
d) Đúng. \(f(40000) = 2000000\) nên nếu bán 40000 đồng/quả thì lợi nhuận theo ngày là 2000000 đồng.
Một xí nghiệp may áo vest và quần âu để chuẩn bị cho dịp cuối năm. Biết may 1 áo vest hết 2m vải và cần 20 giờ; may 1 quần âu hết 1,5m vải và cần 5 giờ. Xí nghiệp được giao sử dụng không quá 900m vải và 60 giờ công không vượt quá 6000 giờ. Theo khảo sát thị trường, số lượng quần âu bán ra không nhỏ hơn số lượng áo vest bán ra và số lượng quần áo bán ra không vượt quá 2 lần số lượng áo vest bán ra. Khi xuất ra thị trường, 1 chiếc áo vest là 350 nghìn đồng, 1 chiếc quần âu là 100 nghìn đồng. Gọi x, y lần lượt là số áo vest và quần âu xí nghiệp có sẽ sản xuất. Tính giá trị của biểu thức T = 2x + 3y.
Đáp án:
Đáp án:
Ứng dụng miền nghiệm của hệ bất phương trình bậc nhất hai ẩn để giải bài toán.
Số mét vải để may x áo và y quần là: 2x + 1,5y (m).
Vì xí nghiệp được giao sử dụng không quá 900 m vải nên ta có: \(2x + 1,5y \le 900\).
Số giờ để may x áo và y quần là: 20x + 5y (giờ).
Vì số giờ công không vượt quá 6000 giờ nên ta có: \(20x + 5y \le 600\) hay \(4x + y \le 1200\).
Theo khảo sát thị trường, ta có:
Số lượng quần bán ra không nhỏ hơn số lượng áo nên \(y \ge x\).
Số lượng quần không vượt quá 2 lần số lượng áo nên \(y \le 2x\).
Ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}2x + 1,5y \le 900\\4x + y \le 1200\\x \le y\\2x \ge y\\x \ge 0\\y \ge 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}2x + 1,5y \le 900\\4x + y \le 1200\\x - y \le 0\\2x - y \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)
Ta biểu diễn miền nghiệm:
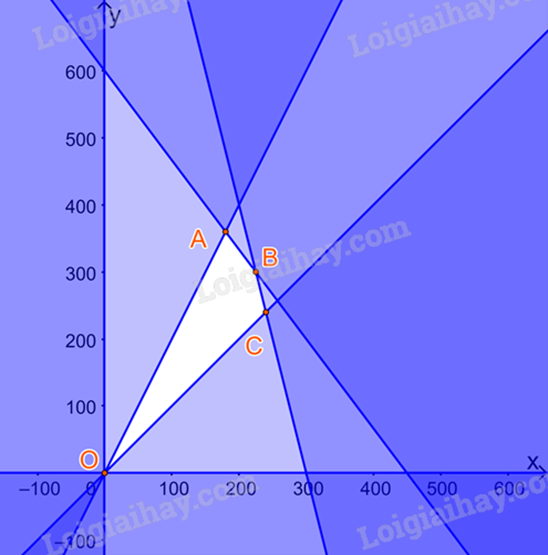
Miền nghiệm của hệ bất phương trình là tứ giác OABC với O(0;0), A(180;360), B(200;250), C(240;240).
Tiền lãi khi bán x cái áo và y cái quần là 350x + 100y (nghìn đồng).
Đặt F = 350x + 100y.
Ta có biểu thức F = 350x + 100y có giá trị lớn nhất tại một trong các đỉnh của tứ giác OABC.
Tính giá trị biểu thức T tại các đỉnh của tứ giác:
Tại O(0;0), với x = 0 và y = 0 thì F = 350.0 + 100.0 = 0;
Tại A(180;360), với x = 180 và y = 360 thì F = 350.180 + 100.360 = 99000.
Tại B(225;300), với x = 225 và y = 300 thì F = 350.225 + 100.300 = 108750.
Tại C(240;240), với x = 240 và y = 240 thì F = 350.240 + 100.240 = 108000.
Ta được F đạt giá trị lớn nhất bằng 108750 000 đồng khi x = 225, y = 300.
Vậy để thu được tiền lãi là cao nhất thì phân xưởng cần may 225 cái áo vest, 300 cái quần âu.
T = 2.225 + 3.300 = 1350.
Trong không gian Oxyz, cho tam giác ABC biết A(1;-1;2), B(-2;0;3), C(0;1;-2). Gọi M(a;b;c) là điểm thuộc mặt phẳng (Oxy) sao cho biểu thức đạt giá trị nhỏ nhất. Tính giá trị của biểu thức T = 12a + 12b + c.
Đáp án:
Đáp án:
Áp dụng các quy tắc cộng, trừ vecto, tích vô hướng của hai vecto. Đưa biểu thức về dạng hằng đẳng thức để tìm giá trị nhỏ nhất.
Vì \(M(a;b;c) \in (Oxy)\) nên M(a;b;0).
\(\overrightarrow {MA} = (1 - a; - 1 - b;2)\); \(\overrightarrow {MB} = ( - 2 - a; - b;3)\); \(\overrightarrow {MC} = ( - a; - b; - 2)\).
\(\overrightarrow {MA} .\overrightarrow {MB} = (1 - a)( - 2 - a) + ( - 1 - b)( - b) + 6 = {a^2} + a + {b^2} + b + 4\).
\(\overrightarrow {MB} .\overrightarrow {MC} = ( - 2 - a)( - a) + ( - b)( - 1 - b) - 6 = {a^2} + 2a + {b^2} - b - 6\).
\(\overrightarrow {MC} .\overrightarrow {MA} = ( - a)(1 - a) + (1 - b)( - 1 - b) - 4 = {a^2} - a + {b^2} - 5\).
\(S = {a^2} + a + {b^2} + b + 4 + 2\left( {{a^2} + 2a + {b^2} - b - 6} \right) + 3\left( {{a^2} - a + {b^2} - 5} \right) = 6{a^2} + 2a + 6{b^2} - b - 23\)
\( = 6{\left( {a + \frac{1}{6}} \right)^2} + 6{\left( {b - \frac{1}{{12}}} \right)^2} - \frac{{557}}{{24}} \ge - \frac{{557}}{{24}}\).
Dấu “=” xảy ra khi \(a = - \frac{1}{6}\) và \(b = \frac{1}{{12}}\).
Khi đó \(T = 12a + 12b + c = 12.\left( { - \frac{1}{6}} \right) + 12.\frac{1}{{12}} + 0 = - 1\).
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 1 và thể tích bằng \(\frac{2}{3}\). Gọi G là trọng tâm của tam giác SCD. Trên các cạnh AB, SD, lần lượt lấy các điểm E, F sao cho EF song song BG. Khoảng cách giữa hai đường thẳng DG và EF bằng \(\frac{m}{n}\) với m, n nguyên dương \(\frac{m}{n}\) là phân số tối giản. Tính giá trị của biểu thức T = 2m – n.
Đáp án:
Đáp án:
Tính khoảng cách thông qua thể tích và diện tích khối chóp.
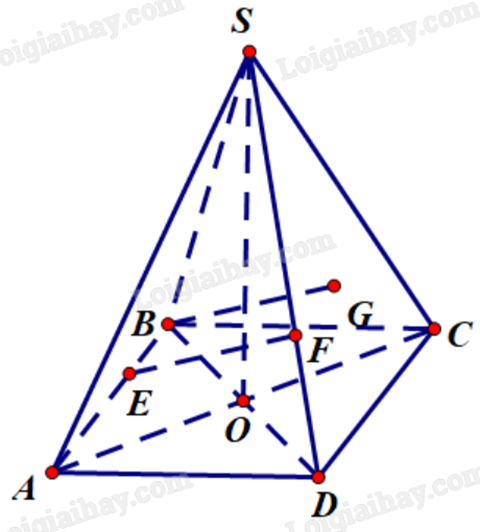
EF // BG nên E, F, G, B đồng phẳng.
\(\left\{ \begin{array}{l}(EFGB) \cap (SCD) = GF\\(EFGB) \cap (ABCD) = EB\\(SCD) \cap (ABCD) = CD\\EB//CD\end{array} \right.\) nên GF // EB // CD.
\(d(DG,EF) = d(EF,(BGD)) = d(E,(BGD)) = \frac{{3{V_{G.EBD}}}}{{{S_{BGD}}}}\).
\({V_{G.BED}} = \frac{1}{3}d(G,(BED)).{S_{BED}} = \frac{1}{3}.\frac{1}{3}d(S,(ABCD)).{S_{BED}}\).
Do EBGF là hình bình hành nên \(\frac{{EB}}{{AB}} = \frac{{GF}}{{CD}} = \frac{{GF}}{{2MD}} = \frac{1}{2}.\frac{{SG}}{{SM}} = \frac{1}{3}\).
Khi đó \({S_{BED}} = \frac{1}{3}{S_{BAD}} = \frac{1}{6}{S_{ABCD}}\).
\({V_{G.BED}} = \frac{1}{3}.\frac{1}{3}d(S,(ABCD)).\frac{1}{6}{S_{ABCD}} = \frac{1}{{18}}.\frac{2}{3} = \frac{1}{{27}}\).
\(BD = \sqrt 2 \); \({V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} \Leftrightarrow SO = \frac{{3.{V_{S.ABCD}}}}{{{S_{ABCD}}}} = \frac{{3.\frac{2}{3}}}{{{1^2}}} = 2\).
\(SB = \sqrt {S{O^2} + O{B^2}} = \sqrt {{2^2} + \left( {\frac{{\sqrt 2 }}{2}} \right)} = \frac{{3\sqrt 2 }}{2}\).
\(BM = \sqrt {B{C^2} + C{M^2}} = \sqrt {{1^2} + {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 5 }}{2}\).
\(SM = \sqrt {S{O^2} + O{M^2}} = \sqrt {{2^2} + {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt {17} }}{2} \Rightarrow GM = \frac{{\sqrt {17} }}{6}\).
\(B{G^2} = G{M^2} + B{M^2} - 2.BM.GM.\cos \widehat {GMB} \)
\(= G{M^2} + B{M^2} - 2.BM.GM.\frac{{M{S^2} + M{B^2} - S{B^2}}}{{2.MS.MB}} = \frac{{25}}{{18}}\).
\(BG = \frac{{5\sqrt 2 }}{6}\).
\(GD = \sqrt {G{M^2} + M{D^2}} = \sqrt {{{\left( {\frac{{\sqrt {17} }}{6}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt {26} }}{6}\).
\(p = \frac{{BG + GD + DB}}{2} = \frac{{\sqrt {26} + 11\sqrt 2 }}{{12}}\).
Áp dụng công thức Heron: \({S_{BGD}} = \frac{1}{2}\).
\(d(DG,EF) = \frac{{3{V_{G.EBD}}}}{{{S_{BGD}}}} = \frac{{3.\frac{1}{{27}}}}{{\frac{1}{2}}} = \frac{2}{9} = \frac{m}{n}\).
Vậy T = 2m – n = 2.2 – 9 = -5.
Người ta muốn xây một bể chứa nước lớn dạng một khối hộp chữ nhật không nắp (xây bốn mặt xung quanh và mặt đáy) có thể tích lớn hơn 432 \({m^3}\) nước. Đây là bể hình chữ nhật có chiều dài gấp đôi chiều rộng, tính chi phí xây bể là 400.000 đồng/\({m^2}\) (tính trên diện tích mặt trong bể). Hỏi chi phí thấp nhất để xây bể là bao nhiêu triệu đồng (kết quả làm tròn đến hàng đơn vị)?
Đáp án:
Đáp án:
Đặt ẩn x là chiều dài hoặc chiều rộng của bể. Lập hàm số tính chi phí xây bể theo x và tìm giá trị nhỏ nhất.
Gọi chiều rộng đáy bể là x (m), khi đó chiều dài đáy bể là 2x (m) với điều kiện \(x > 0\).
Diện tích đáy bể là \(2{x^2}\) \(({m^2})\).
Chiều cao bể là \(\frac{{432}}{{2{x^2}}} = \frac{{216}}{{{x^2}}}\) (m).
Diện tích xung quanh bể là \(2.\frac{{216}}{{{x^2}}}x + 2.\frac{{216}}{{{x^2}}}2x = \frac{{432}}{x} + \frac{{864}}{x} = \frac{{1296}}{x}\) (m).
Chi phí xây bể là \(f(x) = \left( {2{x^2} + \frac{{1296}}{x}} \right).400000 = 800000{x^2} + \frac{{518400000}}{x}\) (đồng).
\(f'(x) = 1600000x - \frac{{518400000}}{{{x^2}}} = 0 \Leftrightarrow {x^3} = 324 \Leftrightarrow x = \sqrt[3]{{324}}\) (m).
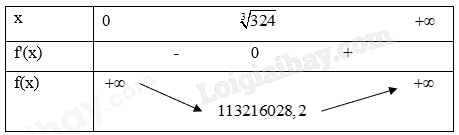
Vậy chi phí thấp nhất để xây bể là \(f(\sqrt[3]{{324}}) \approx 113216028,2\) đồng, hay xấp xỉ 113 triệu đồng.
Một công ty kinh doanh dịch vụ nhận thấy rằng: Nếu áp dụng mức giá 3 triệu đồng/người/ngày thì mỗi tháng có 160 khách đến nghỉ và mỗi khách sẽ nghỉ 10 ngày. Nếu có tăng giá thêm 500 nghìn đồng/người/ngày thì mỗi tháng sẽ có khách đến nghỉ sẽ giảm 4 người và thời gian lưu trú của mỗi người khách cũng giảm đi 2 ngày. Ngược lại, nếu công ty giữ nguyên mức giá 500 nghìn đồng/người/ngày thì hàng tháng số khách đến nghỉ sẽ tăng thêm 4 người và thời gian lưu trú của một khách cũng tăng thêm 2 ngày. Hỏi công ty cần áp dụng mức giá bao nhiêu triệu đồng/người/ngày để lợi nhuận tháng thu được là lớn nhất, biết tổng chi phí công ty phải chi cho một ngày lưu trú của mỗi khách là 2 triệu đồng và Sở du lịch không cho công ty thu vượt quá 10 triệu đồng/người/ngày?
Đáp án:
Đáp án:
Giả sử mức giá tăng lên/giảm đi là x. Lập hàm số theo x biểu diễn lợi nhuận của công ty và tìm giá trị lón nhất.
Giả sử mức giá một người, một ngày là 3 + 0,5x (\(2 \le 3 + 0,5x \le 10 \Leftrightarrow - 2 \le x \le 14)\).
Khi đó số khách là 160 – 4x, thời gian lưu trú là 10 – 2x.
Tổng doanh thu là \((3 + 0,5x)(160 - 4x)(10 - 2x)\).
Tổng chi phí là \(2(160 - 4x)(10 - 2x)\).
Vậy lợi nhuận là \(f(x) = (1 + 0,5x)(160 - 4x)(10 - 2x) = 4{x^3} - 172{x^2} + 440x + 1600\).
\(f'(x) = 12{x^2} - 344x + 440 = 0\) khi \(x = \frac{{43 - 7\sqrt {31} }}{3}\) (giá trị duy nhất thỏa mãn điều kiện).
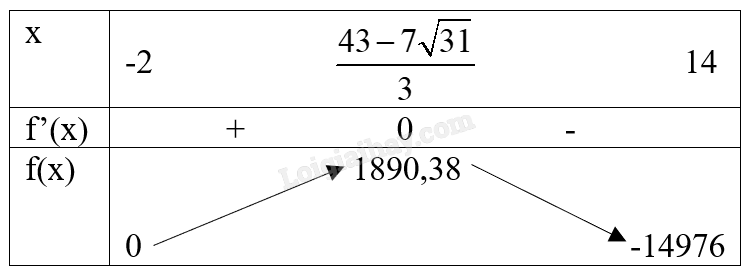
Vậy, để lợi nhuận lớn nhất thì \(x = \frac{{43 - 7\sqrt {31} }}{3}\), khi đó giá tiền cần áp dụng là \(3 + 0,5x = 3 + 0,5.\frac{{43 - 7\sqrt {31} }}{3} \approx 3,67\) triệu đồng.
Cho \(\cot \alpha = \frac{1}{3}\). Biết giá trị của biểu thức \(\frac{{3\sin \alpha + 4\cos \alpha }}{{2\sin \alpha - 5\cos \alpha }}\) có dạng \(\frac{a}{b}\) (với \(a,b \in \mathbb{N}\); \(b \ne 0\), \(\frac{a}{b}\) là phân số tối giản). Tính giá trị của biểu thức T = 100a + b.
Đáp án:
Đáp án:
Chia cả tử và mẫu của biểu thức cho \(\cos \alpha \).
Vì \(\cot \alpha = \frac{1}{3}\) nên \(\cos \alpha \ne 0\).
\(P = \frac{{3\sin \alpha + 4\cos \alpha }}{{2\sin \alpha - 5\cos \alpha }} = \frac{{3 + 4\cot \alpha }}{{2 - 5\cot \alpha }} = \frac{{3 + 4.\frac{1}{3}}}{{2 - 5.\frac{1}{3}}} = 13\).
Vậy T = 100.13 + 1 = 1301.
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
Các bài khác cùng chuyên mục
- Đề thi thử THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
- Đề thi THPT môn Toán năm 2025 (Mã 123) có lời giải
- Đề tham khảo thi THPT môn Toán - Đề số 10 (hay, chi tiết)
- Đề khảo sát chất lượng Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội
- Đề thi thử THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
- Đề thi THPT môn Toán năm 2025 (Mã 123) có lời giải
- Đề tham khảo thi THPT môn Toán - Đề số 10 (hay, chi tiết)
- Đề khảo sát chất lượng Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội