-
Đề thi chính thức tốt nghiệp THPT môn Toán
-
Đề thi thử tốt nghiệp THPT môn Toán
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Vĩnh Phúc
- Đề thi thử tốt nghiệp THPT môn Toán năm 2025 Sở GD Hà Tĩnh
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Ninh Bình
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 3 - Thanh Hóa
- Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2025 cụm các trường số 4 - Hải Dương
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Phú Thọ
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 4 - Thanh Hóa
- Đề thi thử tốt nghiệp THPT môn Toán năm 2025 Sở GD Quảng Bình
- Đề KSCL Toán 11 năm 2024 - 2025 sở GD&ĐT Hà Nội
- Đề KSCL Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội
-
Đề tham khảo thi tốt nghiệp THPT môn Toán
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 1
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 2
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 3
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 4
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 5
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 6
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 7
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 8
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 9
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 10
Đề tham khảo thi THPT môn Toán - Đề số 10 (hay, chi tiết)
I. Phần trắc nghiệm
Đề bài
Nguyên hàm của hàm số y = sinx + 2cosx là
-
A.
cosx – 2sinx + C
-
B.
-cosx + 2sinx + C
-
C.
cosx + 2sinx + C
-
D.
-cosx – 2sinx + C
Thể tích khối tròn xoay do hình phẳng được giới hạn bởi các đường \(y = \sqrt x \), trục Ox và hai đường thẳng x = 1, x = 4 khi quay quanh trục hoành được tính bởi công thức nào?
-
A.
\(V = \pi \int\limits_1^4 {xdx} \)
-
B.
\(V = \int\limits_1^4 {\left| {\sqrt x } \right|dx} \)
-
C.
\(V = {\pi ^2}\int\limits_1^4 {xdx} \)
-
D.
\(V = \pi \int\limits_1^4 {\sqrt x dx} \)
Tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) được thống kê lại như sau:
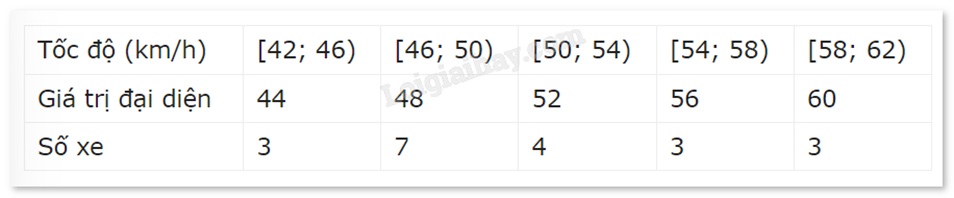
Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm.
-
A.
26,56
-
B.
5,154
-
C.
7,23
-
D.
25,32
Trong không gian Oxy, cho mặt phẳng \(\left( \alpha \right)\): x + 2y – 2z + 3 = 0. Phương trình tham số của đường thẳng đi qua điểm A(2;1;-5) và vuông góc với mặt phẳng \(\left( \alpha \right)\) là
-
A.
\(\left\{ \begin{array}{l}x = - 2 + t\\y = - 1 + 2t\\z = 5 - 2t\end{array} \right.\) \((t \in \mathbb{R})\)
-
B.
\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + t\\z = - 2 - 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
C.
\(\left\{ \begin{array}{l}x = 2 + t\\y = 1 + 2t\\z = - 5 - 2t\end{array} \right.\) \((t \in \mathbb{R})\)
-
D.
\(\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = - 5 - 2t\end{array} \right.\) \((t \in \mathbb{R})\)
Xác định m để mặt phẳng (P): 3x – 4y + 2z + m = 0 đi qua điểm A(3;1;-2).
-
A.
m = -1
-
B.
m = 1
-
C.
m = 9
-
D.
m = -9
Tập nghiệm của bất phương trình \({\left( {\frac{1}{3}} \right)^x} > 9\) là
-
A.
\(\left( {2;\, + \infty } \right)\)
-
B.
\(\left( { - \infty ;\, - 2} \right)\)
-
C.
\(\left( { - 2;\, + \infty } \right)\)
-
D.
\(\left( { - 2;\,0} \right)\)
Nghiệm của phương trình \({\log _2}x = 3\) là
-
A.
x = 3
-
B.
x = 2
-
C.
x = \({3^2}\)
-
D.
x = \({2^3}\)
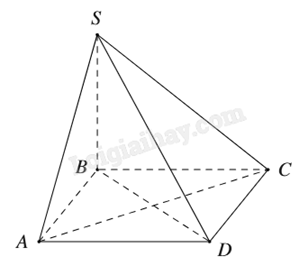
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB vuông góc với mặt phẳng. Khẳng định nào sau đây đúng?
-
A.
\(AC \bot (SCD)\)
-
B.
\(AC \bot (SBD)\)
-
C.
\(AC \bot (SBC)\)
-
D.
\(AC \bot (SAB)\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\), công sai d = 2. Số hạng thứ 5 của \(\left( {{u_n}} \right)\) bằng
-
A.
14
-
B.
5
-
C.
6
-
D.
11
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 4}}{{x - 1}}\) là đường thẳng
-
A.
x = 2
-
B.
x = 1
-
C.
y = 2
-
D.
y = 1
-
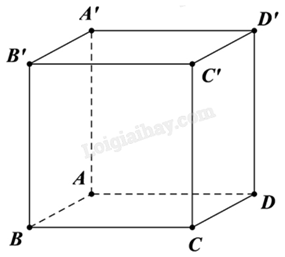
A.
\(\overrightarrow {AB} = \overrightarrow {CD} \)
-
B.
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
-
C.
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
-
D.
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
-
A.
-2
-
B.
-3
-
C.
3
-
D.
2
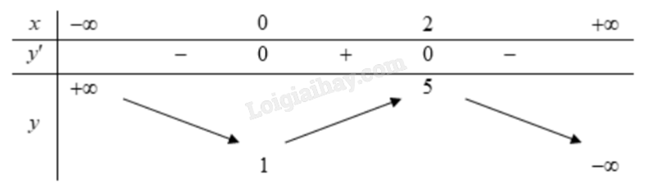
a) Hàm số đồng biến trên khoảng (1;5).
b) Hàm số đạt cực đại tại điểm x = 2.
c) a > 0.
d) Phương trình 2f(x) – e = 0 luôn có một nghiệm âm.
Một người điều khiển ô tô đang ở đường dẫn muốn nhập làn vào đường cao tốc. Khi ô tô cách điểm nhập làn 240 m, tốc độ của ô tô là 28,8 km/h. Bốn giây sau đó, ô tô bắt đầu tăng tốc với tốc độ \(v = at + b\) (m/s) với \(a,b \in \mathbb{R}\), a > 0, trong đó t là thời gian tính bằng giây kể từ khi bắt đầu tăng tốc. Biết rằng ô tô nhập làn cao tốc sau 16 giây và duy trì sự tăng tốc trong 30 giây kể từ khi bắt đầu tăng tốc.
a) Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 208 m.
b) Giá trị của b là 8.
c) Quãng đường S(t) (đơn vị: mét) mà ô tô đi được trong thời gian t giây \((0 \le t \le 30)\) kể từ khi tăng tốc được tính theo công thức \(S(t) = \int\limits_0^{30} {v(t)dt} \).
d) Sau 30 giây kể từ khi tăng tốc, tốc độ của ô tô không vượt quá tốc độ tối đa cho phép là 100 km/h.
Giả sử 5% email của bạn nhận được là email rác. Bạn sử dụng một hệ thống lọc email rác mà khả năng lọc đúng email rác của hệ thống này là 95% và có 10% những email không phải là email rác nhưng vẫn bị lọc.
a) Xác suất nhận được một email rác là 0,05.
b) Xác suất bị lọc của email rác là 0,93.
c) Xác suất email bị lọc bất kể có là rác hay không là 0,1425.
d) Xác suất một email bị lọc thực sự là email rác là \(\frac{7}{{19}}\).
Hải đăng là một ngọn tháp được thiết kế để chiếu sáng từ một hệ thống đèn và thấu kính hoặc thời xưa là chiếu sáng bằng lửa, với mục đích hỗ trợ cho các hoa tiêu trên biển định hướng và tìm đường. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là một mét), coi một phần mặt biển được khảo sát là mặt phẳng (Oxy), trục Oz hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao 50 mét so với mực nước biển, biết đỉnh ở vị trí I(21;35;50). Biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.
a) Phương trình mặt cầu để mô tả ranh giới của vùng phủ sáng trên biển của ngọn hải đăng trên là \({\left( {x - 21} \right)^2} + {\left( {y - 35} \right)^2} + {\left( {z - 50} \right)^2} = 16\).
b) Người đi biển coi là một điểm ở vị trí D(5121;658;0) thì có thể nhìn thấy được ánh sáng của ngọn hải đăng trên.
c) Ngọn hải đăng phủ một vùng sáng trên mặt biển thì bán kính vùng sáng này là 3999,7 (làm tròn đến hàng phần mười của mét) giả sử yếu tố bị che khuất bởi địa hình là không đáng kể).
d) Giả sử người đi biển coi là một điểm từ vị trí D(5121;658;0) di chuyển theo đường thẳng đến chân ngọn hải đăng với tốc độ 7 hải lý/giờ (biết 1 hải lý bằng 1852 mét) thì mất 5,28 phút (kết quả làm tròn đến hàng phần trăm) để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên.
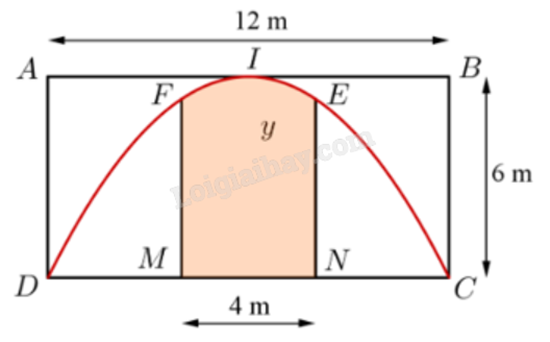
Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Diện tích nhỏ nhất có thể giăng lưới là bao nhiêu mét vuông, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
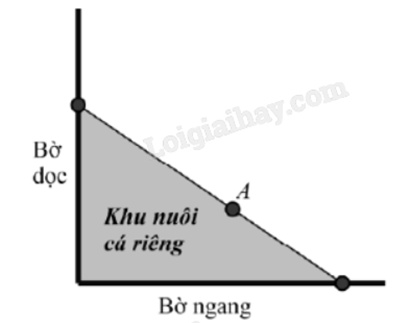
Một công ty quảng cáo muốn làm một bức tranh trang trí hình MNEIF ở chính giữa của một bức tường hình chữ nhật ABCD có chiều cao BC = 6 m, chiều dài CD = 12 m (hình vẽ bên). Cho biết MNEF là hình chữ nhật có MN = 4 m, cung EIF có hình dạng là một phần của parabol có đỉnh I là trung điểm của cạnh AB và đi qua 2 điểm C, D. Đơn giá làm bức tranh là 900 000 đồng/\({m^2}\). Hỏi công ty đó cần bao nhiêu tiền để làm bức tranh đó (đơn vị: triệu đồng)?
Có hai đội thi đấu môn bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I (làm tròn đến hai chữ số thập phân).
Trong không gian Oxyz, một cabin cáp treo ở Bà Nà Hill xuất phát từ điểm A(-2;1;5) và chuyển động đều theo đường cáp có vecto chỉ phương là \(\overrightarrow u = (0; - 2;6)\) với tốc độ là 4 m/s (đơn vị trên mỗi trục tọa độ là mét). Giả sử sau 5 giây (s) kể từ lúc xuất phát, cabin đến điểm M. Gọi tọa độ M(a;b;c). Tính a + 3b + c.
Trong tiết thể dục học về kĩ thuật chuyền bóng hơi, Thanh và Minh đang tập chuyền bóng cho nhau. Thanh ném bóng cho Minh đỡ, quả bóng bay lên cao nhưng lại lệch sang phải của Thanh và rơi xuống vị trí cách Minh 0,5 (m) và cách Thanh 4,5 (m) được mô tả bằng hình vẽ bên dưới.
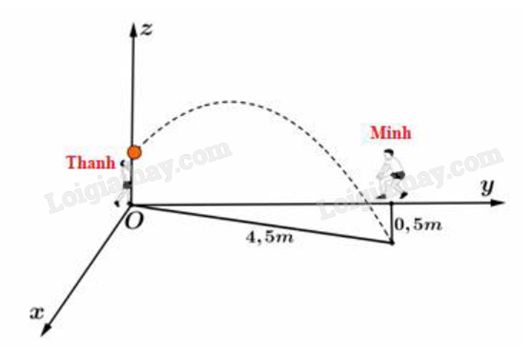
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng \(\left( \alpha \right)\): ax + by + cz + d = 0 và vuông góc với mặt đát. Khoảng cách từ bạn Minh đến mặt phẳng \(\left( \alpha \right)\) bằng bao nhiêu mét (làm tròn kết quả đến chữ số thập phân thứ hai)?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(\sqrt 3 \). Gọi M, N và P lần lượt là trung điểm của các cạnh AB, AD và DC. Gọi H là giao điểm của CN và DM, biết SH vuông góc với (ABCD), SH = 3. Tính khoảng cách từ điểm C đến mặt phẳng (SBP).
Lời giải và đáp án
Nguyên hàm của hàm số y = sinx + 2cosx là
-
A.
cosx – 2sinx + C
-
B.
-cosx + 2sinx + C
-
C.
cosx + 2sinx + C
-
D.
-cosx – 2sinx + C
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lượng giác \(\int {\cos xdx} = \sin x + C\), \(\int {\sin xdx} = - \cos x + C\).
\(\int {(\sin x + 2\cos x)dx} = - \cos x + 2\sin x + C\).
Thể tích khối tròn xoay do hình phẳng được giới hạn bởi các đường \(y = \sqrt x \), trục Ox và hai đường thẳng x = 1, x = 4 khi quay quanh trục hoành được tính bởi công thức nào?
-
A.
\(V = \pi \int\limits_1^4 {xdx} \)
-
B.
\(V = \int\limits_1^4 {\left| {\sqrt x } \right|dx} \)
-
C.
\(V = {\pi ^2}\int\limits_1^4 {xdx} \)
-
D.
\(V = \pi \int\limits_1^4 {\sqrt x dx} \)
Đáp án : A
Cho hàm số \(y = f(x)\) liên tục trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức \(V = \pi \int\limits_a^b {{f^2}(x)dx} \).
Thể tích khối tròn xoay khi quay hình phẳng quanh trục Ox được tính theo công thức \(V = \pi \int\limits_1^4 {{{\left( {\sqrt x } \right)}^2}dx} = \pi \int\limits_1^4 {xdx} \).
Tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) được thống kê lại như sau:
Hãy tính độ lệch chuẩn của mẫu số liệu ghép nhóm.
-
A.
26,56
-
B.
5,154
-
C.
7,23
-
D.
25,32
Đáp án : B
Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm.
Số trung bình của mẫu số liệu là:
\(\overline x = \frac{{3.44 + 7.48 + 4.52 + 3.56 + 3.60}}{{20}} = 51,2\).
Phương sai của mẫu số liệu là:
\({s^2} = \frac{1}{{20}}\left[ {3.{{(44 - 51,2)}^2} + 7.{{(48 - 51,2)}^2} + 4.{{(52 - 51,2)}^2} + 3.{{(56 - 51,2)}^2} + 3.{{(60 - 51,2)}^2}} \right] = 26,56\).
Độ lệch chuẩn của mẫu số liệu ghép nhóm là:
\(s = \sqrt {{s^2}} = \sqrt {26,56} \approx 5,154\).
Trong không gian Oxy, cho mặt phẳng \(\left( \alpha \right)\): x + 2y – 2z + 3 = 0. Phương trình tham số của đường thẳng đi qua điểm A(2;1;-5) và vuông góc với mặt phẳng \(\left( \alpha \right)\) là
-
A.
\(\left\{ \begin{array}{l}x = - 2 + t\\y = - 1 + 2t\\z = 5 - 2t\end{array} \right.\) \((t \in \mathbb{R})\)
-
B.
\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 + t\\z = - 2 - 5t\end{array} \right.\) \((t \in \mathbb{R})\)
-
C.
\(\left\{ \begin{array}{l}x = 2 + t\\y = 1 + 2t\\z = - 5 - 2t\end{array} \right.\) \((t \in \mathbb{R})\)
-
D.
\(\left\{ \begin{array}{l}x = 2 - t\\y = 1 + 2t\\z = - 5 - 2t\end{array} \right.\) \((t \in \mathbb{R})\)
Đáp án : C
Đường thẳng đi qua điểm \(M({x_0};{y_0};{z_0})\) có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) có phương trình là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\).
Vì đường thẳng vuông góc với \(\left( \alpha \right)\) nên vecto pháp tuyến của \(\left( \alpha \right)\) là một vecto chỉ phương của đường thẳng.
Phương trình đường thẳng nhận \(\overrightarrow u = (1;2; - 2)\) làm vecto chỉ phương và đi qua điểm A(2;1;-5) là \(\left\{ {\begin{array}{*{20}{c}}{x = 2 + t}\\{y = 1 + 2t}\\{z = - 5 - 2t}\end{array}} \right.\) \((t \in \mathbb{R})\).
Xác định m để mặt phẳng (P): 3x – 4y + 2z + m = 0 đi qua điểm A(3;1;-2).
-
A.
m = -1
-
B.
m = 1
-
C.
m = 9
-
D.
m = -9
Đáp án : A
Thay tọa độ điểm A vào phương trình (P) rồi giải, tìm m.
Ta có \(3.3 - 4.1 + 2.( - 2) + m = 0 \Leftrightarrow m = - 1\).
Tập nghiệm của bất phương trình \({\left( {\frac{1}{3}} \right)^x} > 9\) là
-
A.
\(\left( {2;\, + \infty } \right)\)
-
B.
\(\left( { - \infty ;\, - 2} \right)\)
-
C.
\(\left( { - 2;\, + \infty } \right)\)
-
D.
\(\left( { - 2;\,0} \right)\)
Đáp án : B
Với 0 < a < 1 thì \({a^x} > b \Leftrightarrow x < {\log _a}b\).
\({\left( {\frac{1}{3}} \right)^x} > 9 \Leftrightarrow x < {\log _{\frac{1}{3}}}9 \Leftrightarrow x < - 2\). Vậy tập nghiệm \(S = \left( { - \infty ;\, - 2} \right)\).
Nghiệm của phương trình \({\log _2}x = 3\) là
-
A.
x = 3
-
B.
x = 2
-
C.
x = \({3^2}\)
-
D.
x = \({2^3}\)
Đáp án : D
ĐKXĐ: x > 0.
\({\log _a}x = b \Leftrightarrow x = {a^b}\).
ĐKXĐ: x > 0.
\({\log _2}x = 3 \Leftrightarrow x = {2^3}\) (thỏa mãn).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SB vuông góc với mặt phẳng. Khẳng định nào sau đây đúng?
-
A.
\(AC \bot (SCD)\)
-
B.
\(AC \bot (SBD)\)
-
C.
\(AC \bot (SBC)\)
-
D.
\(AC \bot (SAB)\)
Đáp án : B
Đường thẳng vuông góc với mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng.
Vì ABCD là hình vuông nên \(AC \bot BD\).
Mặt khác \(SB \bot (ABCD)\) nên \(SB \bot AC\).
Do đó \(AC \bot (SBD)\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\), công sai d = 2. Số hạng thứ 5 của \(\left( {{u_n}} \right)\) bằng
-
A.
14
-
B.
5
-
C.
6
-
D.
11
Đáp án : D
Áp dụng công thức số hạng tổng quát của cấp số cộng: \({u_n} = {u_1} + (n - 1)d\).
\({u_5} = 3 + (5 - 1).2 = 11\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 4}}{{x - 1}}\) là đường thẳng
-
A.
x = 2
-
B.
x = 1
-
C.
y = 2
-
D.
y = 1
Đáp án : C
Đồ thị hàm số y = f(x) có đường tiệm cận ngang là \(y = {y_0}\) nếu thõa mãn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\).
Ta có \(\mathop {\lim }\limits_{x \to \pm \infty } \frac{{2x + 4}}{{x - 1}} = 2\) nên đồ thị hàm số có đường tiệm cận ngang là y = 2.
-
A.
\(\overrightarrow {AB} = \overrightarrow {CD} \)
-
B.
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
-
C.
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
-
D.
\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|\)
Đáp án : A
Áp dụng định nghĩa hai vecto bằng nhau, quy tắc ba điểm, quy tắc hình hộp và độ dài vecto.
Vì \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng nên \(\overrightarrow {AB} \ne \overrightarrow {CD} \).
-
A.
-2
-
B.
-3
-
C.
3
-
D.
2
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Giá trị cực đại của hàm số đã cho bằng 2.
a) Hàm số đồng biến trên khoảng (1;5).
b) Hàm số đạt cực đại tại điểm x = 2.
c) a > 0.
d) Phương trình 2f(x) – e = 0 luôn có một nghiệm âm.
a) Hàm số đồng biến trên khoảng (1;5).
b) Hàm số đạt cực đại tại điểm x = 2.
c) a > 0.
d) Phương trình 2f(x) – e = 0 luôn có một nghiệm âm.
Quan sát bảng biến thiên và nhận xét.
Áp dụng kiến thức về sự tương giao đồ thị.
a) Sai. Hàm số đồng biến trên khoảng (1;2) và nghịch biến trên khoảng (2;5).
b) Đúng. Hàm số đạt cực đại tại điểm x = 2.
c) Sai. Vì \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \) nên hệ số a < 0.
d) Đúng. \(2f(x) - e = 0 \Leftrightarrow f(x) = \frac{e}{2}\).
Phương trình 2f(x) – e = 0 luôn có một nghiệm âm khi đồ thị hàm số y = f(x) cắt đồ thị hàm số \(y = \frac{e}{2}\) tại một điểm có hoành độ âm.
Đồ thị hàm số \(y = \frac{e}{2}\) là đường thẳng song song với trục hoành, được minh họa trên bảng biến thiên như sau:
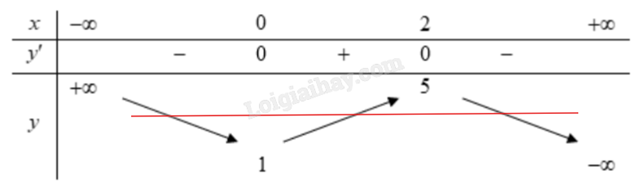
Ta thấy đường thẳng \(y = \frac{e}{2}\) cắt đồ thị y = f(x) tại một điểm có hoành độ âm nên phương trình 2f(x) – e = 0 có một nghiệm âm.
Một người điều khiển ô tô đang ở đường dẫn muốn nhập làn vào đường cao tốc. Khi ô tô cách điểm nhập làn 240 m, tốc độ của ô tô là 28,8 km/h. Bốn giây sau đó, ô tô bắt đầu tăng tốc với tốc độ \(v = at + b\) (m/s) với \(a,b \in \mathbb{R}\), a > 0, trong đó t là thời gian tính bằng giây kể từ khi bắt đầu tăng tốc. Biết rằng ô tô nhập làn cao tốc sau 16 giây và duy trì sự tăng tốc trong 30 giây kể từ khi bắt đầu tăng tốc.
a) Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 208 m.
b) Giá trị của b là 8.
c) Quãng đường S(t) (đơn vị: mét) mà ô tô đi được trong thời gian t giây \((0 \le t \le 30)\) kể từ khi tăng tốc được tính theo công thức \(S(t) = \int\limits_0^{30} {v(t)dt} \).
d) Sau 30 giây kể từ khi tăng tốc, tốc độ của ô tô không vượt quá tốc độ tối đa cho phép là 100 km/h.
a) Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 208 m.
b) Giá trị của b là 8.
c) Quãng đường S(t) (đơn vị: mét) mà ô tô đi được trong thời gian t giây \((0 \le t \le 30)\) kể từ khi tăng tốc được tính theo công thức \(S(t) = \int\limits_0^{30} {v(t)dt} \).
d) Sau 30 giây kể từ khi tăng tốc, tốc độ của ô tô không vượt quá tốc độ tối đa cho phép là 100 km/h.
Ứng dụng tích phân để giải bài toán chuyển động. Áp dụng công thức \(S(t) = \int\limits_0^t {v(t)dt} \).
a) Đúng. Tốc độ ban đầu của ô tô là \(\frac{{28,8}}{{3,6}} = 8\) m/s.
Quãng đường ô tô đi được trong 4 giây đầu tiên là 4.8 = 32 m.
Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 320 – 32 = 208 m.
b) Đúng. Thời điểm bắt đầu tăng tốc ta có \(v(0) = 8 \Leftrightarrow a.0 + b = 8 \Leftrightarrow b = 8\).
c) Sai. Quãng đường S(t) (đơn vị: mét) mà ô tô đi được trong thời gian t giây \((0 \le t \le 30)\) kể từ khi tăng tốc được tính theo công thức \(S(t) = \int\limits_0^t {v(t)dt} \).
d) Đúng. Ta có v(t) = at + 8 (m/s).
Vì xe nhập làn sau 16 giây kể từ lúc tăng tốc nên ta có:
\(208 = \int\limits_0^{16} {(at + 8)dt} \Leftrightarrow 208 = a\frac{{{t^2}}}{2} + 8t\left| {\begin{array}{*{20}{c}}{16}\\0\end{array}} \right. \Leftrightarrow 208 = a\frac{{{{16}^2}}}{2} + 8.16 \Leftrightarrow a = \frac{5}{8}\).
Suy ra \(v(t) = \frac{5}{8}t + 8\) (m/s).
Tốc độ của ô tô sau 30 giây là \(v(30) = \frac{5}{8}.30 + 8 = \frac{{107}}{4}\) (m/s) = 96,3 km/h.
Giả sử 5% email của bạn nhận được là email rác. Bạn sử dụng một hệ thống lọc email rác mà khả năng lọc đúng email rác của hệ thống này là 95% và có 10% những email không phải là email rác nhưng vẫn bị lọc.
a) Xác suất nhận được một email rác là 0,05.
b) Xác suất bị lọc của email rác là 0,93.
c) Xác suất email bị lọc bất kể có là rác hay không là 0,1425.
d) Xác suất một email bị lọc thực sự là email rác là \(\frac{7}{{19}}\).
a) Xác suất nhận được một email rác là 0,05.
b) Xác suất bị lọc của email rác là 0,93.
c) Xác suất email bị lọc bất kể có là rác hay không là 0,1425.
d) Xác suất một email bị lọc thực sự là email rác là \(\frac{7}{{19}}\).
Sử dụng công thức tính xác suất toàn phần và công thức Bayes.
Gọi các biến cố:
A: “Email nhận được là email rác”.
B: “Email bị lọc”.
a) Đúng. Vì 5% email nhận được là email rác nên xác suất nhận được một email rác là 5% = 0,05.
b) Sai. Xác suất bị lọc của email rác là P(B|A) = 95% = 0,95.
c) Đúng. Xác suất email nhận được không phải email rác là \(P(\overline A ) = 1 - P(A) = 1 - 0,05 = 0,95\).
Xác suất email bị lọc không phải email rác là \(P(B|\overline A ) = 10\% = 0,1\).
Xác suất một mail bị lọc bất kể là rác hay không là:
\(P(B) = P(A).P(B|A) + P(\overline A ).P(B|\overline A ) = 0,05.0,95 + 0,95.0,1 = 0,1425\).
d) Sai. Xác suất một email bị lọc thực sự là email rác là:
\(P(A|B) = \frac{{P(A).P(B|A)}}{{P(B)}} = \frac{{0,05.0,95}}{{0,1425}} = \frac{1}{3}\).
Hải đăng là một ngọn tháp được thiết kế để chiếu sáng từ một hệ thống đèn và thấu kính hoặc thời xưa là chiếu sáng bằng lửa, với mục đích hỗ trợ cho các hoa tiêu trên biển định hướng và tìm đường. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục là một mét), coi một phần mặt biển được khảo sát là mặt phẳng (Oxy), trục Oz hướng lên trên vuông góc với mặt biển; một ngọn hải đăng đỉnh cao 50 mét so với mực nước biển, biết đỉnh ở vị trí I(21;35;50). Biết rằng ngọn hải đăng này được thiết kế với bán kính phủ sáng là 4 km.
a) Phương trình mặt cầu để mô tả ranh giới của vùng phủ sáng trên biển của ngọn hải đăng trên là \({\left( {x - 21} \right)^2} + {\left( {y - 35} \right)^2} + {\left( {z - 50} \right)^2} = 16\).
b) Người đi biển coi là một điểm ở vị trí D(5121;658;0) thì có thể nhìn thấy được ánh sáng của ngọn hải đăng trên.
c) Ngọn hải đăng phủ một vùng sáng trên mặt biển thì bán kính vùng sáng này là 3999,7 (làm tròn đến hàng phần mười của mét) giả sử yếu tố bị che khuất bởi địa hình là không đáng kể).
d) Giả sử người đi biển coi là một điểm từ vị trí D(5121;658;0) di chuyển theo đường thẳng đến chân ngọn hải đăng với tốc độ 7 hải lý/giờ (biết 1 hải lý bằng 1852 mét) thì mất 5,28 phút (kết quả làm tròn đến hàng phần trăm) để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên.
a) Phương trình mặt cầu để mô tả ranh giới của vùng phủ sáng trên biển của ngọn hải đăng trên là \({\left( {x - 21} \right)^2} + {\left( {y - 35} \right)^2} + {\left( {z - 50} \right)^2} = 16\).
b) Người đi biển coi là một điểm ở vị trí D(5121;658;0) thì có thể nhìn thấy được ánh sáng của ngọn hải đăng trên.
c) Ngọn hải đăng phủ một vùng sáng trên mặt biển thì bán kính vùng sáng này là 3999,7 (làm tròn đến hàng phần mười của mét) giả sử yếu tố bị che khuất bởi địa hình là không đáng kể).
d) Giả sử người đi biển coi là một điểm từ vị trí D(5121;658;0) di chuyển theo đường thẳng đến chân ngọn hải đăng với tốc độ 7 hải lý/giờ (biết 1 hải lý bằng 1852 mét) thì mất 5,28 phút (kết quả làm tròn đến hàng phần trăm) để đến điểm đầu tiên nhìn thấy được ánh sáng ngọn hải đăng trên.
Áp dụng biểu thức tọa độ các phép toán trong không gian.
Đổi: 4 km = 4000 m.
a) Sai. Phương trình mặt cầu để mô tả ranh giới của vùng phủ sáng trên biển của ngọn hải đăng trên là \({\left( {x - 21} \right)^2} + {\left( {y - 35} \right)^2} + {\left( {z - 50} \right)^2} = {4000^2}\).
b) Sai. Khoảng cách từ người đi biển đến đỉnh ngọn hải đăng là:
\(ID = \sqrt {{{\left( {{x_D} - {x_I}} \right)}^2} + {{\left( {{y_D} - {y_I}} \right)}^2} + {{\left( {{z_D} - {z_I}} \right)}^2}} = \sqrt {{{\left( {5121 - 21} \right)}^2} + {{\left( {658 - 35} \right)}^2} + {{\left( {0 - 50} \right)}^2}} \approx 5138\) (m).
Vì ID > 4000 nên người đi biển không nhìn được ánh sáng của ngọn hải đăng.
c) Đúng. Bán kính vùng sáng trên mặt biển là: \(\sqrt {{{4000}^2} - {{50}^2}} \approx 3999,7\) (m).
d) Sai. Chân ngọn hải đăng là H(21;35;0).
Ta có \(DH = \sqrt {{{(21 - 5121)}^2} + {{(35 - 658)}^2} + {{(0 - 0)}^2}} = \sqrt {{{5100}^2} + {{623}^2}} \).
Khoảng cách từ người đó đến điểm đầu tiên nhìn thấy ánh sáng ngọn hải đăng là:
\(\sqrt {{{5100}^2} + {{623}^2}} - \sqrt {{{4000}^2} - {{50}^2}} \) (m).
Tốc độ di chuyển của người đó là 7 hải lý/giờ = 12964 mét/giờ.
Thời gian để người đó đến điểm đầu tiên nhìn thấy ánh sáng ngọn hải đăng là:
\(\frac{{\sqrt {{{5100}^2} + {{623}^2}} - \sqrt {{{4000}^2} - {{50}^2}} }}{{12964}}.60 \approx 5,27\) (phút).
Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Diện tích nhỏ nhất có thể giăng lưới là bao nhiêu mét vuông, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
Lập hàm biểu diễn diện tích khu nuôi cá theo biến x (với điều kiện của x).
Tìm giá trị nhỏ nhất của hàm số trên.
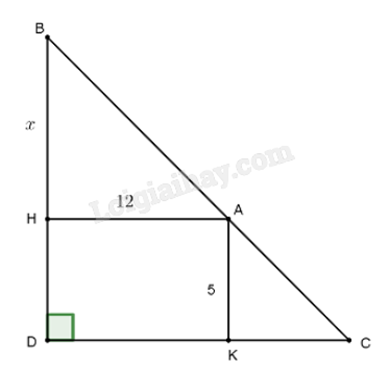
Mô hình hóa bài toán đã cho như hình trên. AH và AK lần lượt là khoảng cách từ A đến bờ dọc BD và bờ ngang CD.
Theo đề bài AH = 12 m, AK = 5 m. Do đó DK = AH = 12 m, DH = AK = 5 m.
Đặt BH = x (m, x > 0).
Vì AH // CD nên \(\frac{{BH}}{{DH}} = \frac{{AB}}{{AC}}\).
Vì AK // BD nên \(\frac{{DK}}{{CK}} = \frac{{AB}}{{AC}}\).
Do đó \(\frac{{BH}}{{DH}} = \frac{{DK}}{{CK}}\left( { = \frac{{AB}}{{AC}}} \right)\), suy ra \(CK = \frac{{DH.DK}}{{BH}} = \frac{{5.12}}{x} = \frac{{60}}{x}\) (m).
Diện tích khu nuôi cá riêng là:
\(S = \frac{1}{2}BD.CD = \frac{1}{2}\left( {x + 5} \right)\left( {12 + \frac{{60}}{x}} \right) = 6x + \frac{{150}}{x} + 60\) \(\left( {{m^2}} \right)\).
Xét hàm \(S(x) = 6x + \frac{{150}}{x} + 60\) với \(x \in \left( {0; + \infty } \right)\):
Ta có \(S'(x) = 6 - \frac{{150}}{{{x^2}}} = 0 \Leftrightarrow x = 5\).
Bảng biến thiên:
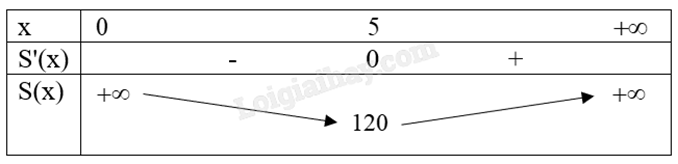
Từ bảng biến thiên, ta có diện tích nhỏ nhất có thể giăng lưới là 120 \({m^2}\).
Một công ty quảng cáo muốn làm một bức tranh trang trí hình MNEIF ở chính giữa của một bức tường hình chữ nhật ABCD có chiều cao BC = 6 m, chiều dài CD = 12 m (hình vẽ bên). Cho biết MNEF là hình chữ nhật có MN = 4 m, cung EIF có hình dạng là một phần của parabol có đỉnh I là trung điểm của cạnh AB và đi qua 2 điểm C, D. Đơn giá làm bức tranh là 900 000 đồng/\({m^2}\). Hỏi công ty đó cần bao nhiêu tiền để làm bức tranh đó (đơn vị: triệu đồng)?
Gắn hệ trục tọa độ ở vị trí phù hợp.
Từ tọa độ các điểm đồ thị đi qua, lập phương trình parabol.
Áp dụng công thức tính diện tích ứng dụng tích phân.
Gắn hệ trục tọa độ với O là trung điểm của MN, các điểm N, C thuộc tia Ox, đỉnh I thuộc tia Oy.
Parabol có phương trình dạng \(y = a{x^2} + bx + c\) (a < 0).
Vì parabol đi qua các điểm I(0;6), C(6;00. D(-6;0) nên ta có:
\(\left\{ \begin{array}{l}6 = a{.0^2} + b.0 + c\\0 = a{.6^2} + b.6 + c\\0 = a{( - 6)^2} + b( - 6) + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{6}\\b = 0\\c = 6\end{array} \right. \Rightarrow y = - \frac{1}{6}{x^2} + 6\).
Diện tích bức tranh là \(S = \int\limits_{ - 2}^2 {\left| { - \frac{1}{6}{x^2} + 6} \right|dx} = \int\limits_{ - 2}^2 {\left( { - \frac{1}{6}{x^2} + 6} \right)dx} = \frac{{208}}{9}\) \(\left( {{m^2}} \right)\).
Số tiền cần dùng là \(\frac{{208}}{9}.900000 = 20800000\) đồng = 20,8 triệu đồng.
Có hai đội thi đấu môn bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên. Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I (làm tròn đến hai chữ số thập phân).
Áp dụng công thức tính xác suất toàn phần và công thức Bayes.
Gọi các biến cố:
A: “Vận động viên được chọn thuộc đội I”.
Suy ra \(\overline A \): “Vận động viên được chọn thuộc đội II”.
B: “Vận động viên được chọn đạt huy chương vàng”.
Đội I có 5 vận động viên, đội II có 7 vận động viên (tổng hai đội là 12 vận động viên) nên ta có \(P(A) = \frac{5}{{12}}\); \(P(\overline A ) = \frac{7}{{12}}\).
Xác suất vận động viên thuộc đội I đạt huy chương vàng là 0,65 nên ta có \(P(B|A) = 0,65\).
Xác suất vận động viên thuộc đội II đạt huy chương vàng là 0,55 nên ta có \(P(B|\overline A ) = 0,65\).
Áp dụng công thức xác suất toàn phần, xác suất vận động viên được chọn đạt huy chương vàng là:
\(P(B) = P(A).P(B|A) + P(\overline A ).P(B|\overline A ) = \frac{5}{{12}}.0,65 + \frac{7}{{12}}.0,55 = \frac{{71}}{{120}}\).
Áp dụng công thức Bayes, xác suất vận động viên đạt huy chương vàng thuộc đội I là:
\(P(A|B) = \frac{{P(A).P(B|A)}}{{P(B)}} = \frac{{\frac{5}{{12}}.0,65}}{{\frac{{71}}{{120}}}} = \frac{{65}}{{142}} \approx 0,46\).
Trong không gian Oxyz, một cabin cáp treo ở Bà Nà Hill xuất phát từ điểm A(-2;1;5) và chuyển động đều theo đường cáp có vecto chỉ phương là \(\overrightarrow u = (0; - 2;6)\) với tốc độ là 4 m/s (đơn vị trên mỗi trục tọa độ là mét). Giả sử sau 5 giây (s) kể từ lúc xuất phát, cabin đến điểm M. Gọi tọa độ M(a;b;c). Tính a + 3b + c.
Lập phương trình đường cáp d và tọa độ điểm M theo tham số t.
Tính AM, từ đó tìm t.
Kết luận tọa độ M và tính a + 3b + c.
Phương trình đường cáp là phương trình đường thẳng d đi qua điểm A(-2;1;5), nhận \(\overrightarrow u = (0; - 2;6)\) làm vecto chỉ phương: \(\left\{ \begin{array}{l}x = - 2\\y = 1 - 2t\\z = 5 + 6t\end{array} \right.\) \(\left( {t \in \mathbb{R}} \right)\).
Vì M thuộc d nên ta có \(M( - 2;1 - 2t;5 + 6t)\).
Cabin đi đến điểm M với tốc độc 4 m/s trong 5 giây. Do đó AM = 4.5 = 20 (m).
Suy ra \(\left| {\overrightarrow {AM} } \right| = 20 \Leftrightarrow \sqrt {{0^2} + {{( - 2t)}^2} + {{(6t)}^2}} = 20 \Leftrightarrow 40{t^2} = {20^2} \Leftrightarrow t = \pm \sqrt {10} \).
Vì \(\overrightarrow {AM} = (0; - 2t;6t)\) cùng hướng với \(\overrightarrow u = (0; - 2;6)\) nên \( - 2t\) và \( - 2\) cùng dấu, suy ra \(t = \sqrt {10} \).
Khi đó \(M( - 2;1 - 2\sqrt 0 ;5 + 6\sqrt {10} )\).
Vậy \(a + 3b + c = - 2 + 3\left( {1 - 2\sqrt {10} } \right) + 5 + 6\sqrt {10} = 6\).
Trong tiết thể dục học về kĩ thuật chuyền bóng hơi, Thanh và Minh đang tập chuyền bóng cho nhau. Thanh ném bóng cho Minh đỡ, quả bóng bay lên cao nhưng lại lệch sang phải của Thanh và rơi xuống vị trí cách Minh 0,5 (m) và cách Thanh 4,5 (m) được mô tả bằng hình vẽ bên dưới.
Biết rằng quỹ đạo của quả bóng nằm trong mặt phẳng \(\left( \alpha \right)\): ax + by + cz + d = 0 và vuông góc với mặt đát. Khoảng cách từ bạn Minh đến mặt phẳng \(\left( \alpha \right)\) bằng bao nhiêu mét (làm tròn kết quả đến chữ số thập phân thứ hai)?
Tìm tọa độ của Minh và vị trí bóng rơi M.
Lập phương trình mặt phẳng \(\left( \alpha \right)\) đi qua gốc tọa độ, nhận \(\overrightarrow n = \left[ {\overrightarrow {OM} ,\overrightarrow k } \right]\) làm vecto pháp tuyến.
Áp dụng công thức tính khoảng cách từ Minh đến \(\left( \alpha \right)\).
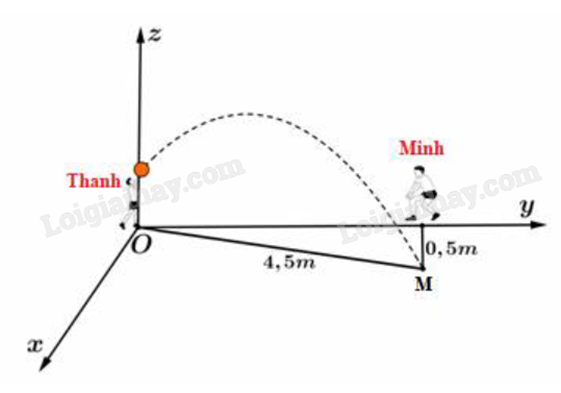
Chọn hệ trục như hình vẽ. Gọi M là điểm mà quả bóng chạm đất.
Khi đó \({x_M} = 0,5\), \({y_M} = \sqrt {4,{5^2} - 0,{5^2}} = 2\sqrt 5 \).
Ta có \(\overrightarrow {OM} = (0,5;2\sqrt 5 ;0)\) và vecto pháp tuyến của (Oxy) là \(\overrightarrow k = (0;0;1)\).
Vì O, M thuộc \(\left( \alpha \right)\) và \(\left( \alpha \right) \bot (Oxy)\) nên giả sử vecto pháp tuyến của \(\left( \alpha \right)\) là \(\overrightarrow n \), ta có:
\(\left\{ \begin{array}{l}\overrightarrow n \bot \overrightarrow {OM} \\\overrightarrow n \bot \overrightarrow k \end{array} \right. \Leftrightarrow \overrightarrow n = \left[ {\overrightarrow {OM} ,\overrightarrow k } \right] = \left( { - 2\sqrt 5 ;0,5;0} \right) = - \frac{1}{2}\left( {4\sqrt 5 ; - 1;0} \right)\).
Phương trình mặt phẳng \(\left( \alpha \right)\) là \(4\sqrt 5 \left( {x - 0} \right) - \left( {y - 0} \right) + 0\left( {z - 0} \right) = 0 \Leftrightarrow 4\sqrt 5 x - y = 0\).
Vị trí bạn Minh có tọa độ là \(\left( {2\sqrt 5 ;0;0} \right)\).
Khoảng cách từ bạn Minh đến mặt phẳng \(\left( \alpha \right)\) là \(\frac{{\left| {4\sqrt 5 .2\sqrt 5 - 1.0 + 0.0} \right|}}{{\sqrt {{{\left( {4\sqrt 5 } \right)}^2} + {{\left( { - 1} \right)}^2} + {0^2}} }} = \frac{{40}}{9} \approx 4,44\) (m).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh \(\sqrt 3 \). Gọi M, N và P lần lượt là trung điểm của các cạnh AB, AD và DC. Gọi H là giao điểm của CN và DM, biết SH vuông góc với (ABCD), SH = 3. Tính khoảng cách từ điểm C đến mặt phẳng (SBP).
Gọi BP giao NC tại F.
Chứng minh \((SBP) \bot (SNC)\).
Xét trong mặt phẳng (SNC), lấy E thuộc SF sao cho \(HE \bot SF\).
Chứng minh \(d\left( {C,(SBP)} \right) = d\left( {H,(SBP)} \right) = HE\).
Áp dụng hệ thức lượng trong tam giác vuông, tính HE.
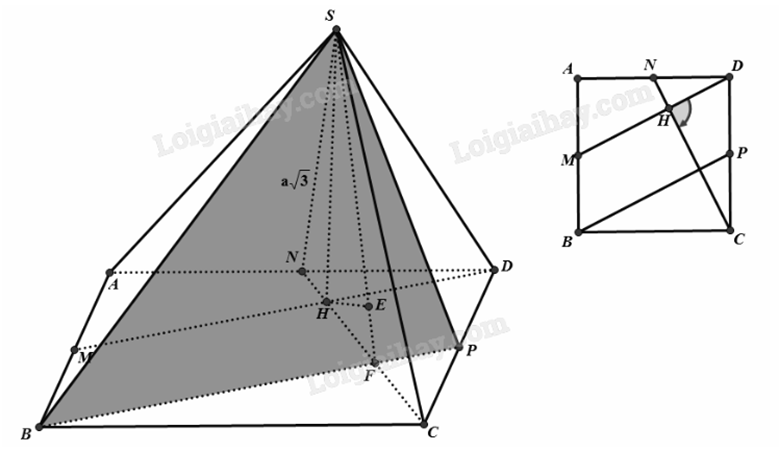
Gọi BP giao NC tại F.
Xét \(\Delta ADM\) và \(\Delta DCN\), có:
\(\widehat {DAM} = \widehat {CDN} = {90^o}\);
AD = CD (cạnh hình vuông);
AM = DN (một nửa cạnh hình vuông).
Do đó \(\Delta ADM = \Delta DCN\)(c.g.c), suy ra \(\widehat {ADM} = \widehat {DCN}\).
Mà \(\widehat {ADM} + \widehat {MDC} = {90^o}\) nên \(\widehat {DCN} + \widehat {MDC} = {90^o} \Rightarrow \widehat {DHC} = {90^o} \Rightarrow NC \bot MD\).
Xét tứ giác BMDP có BM // DP và BM = DP nên BMDP là hình bình hành, suy ra MD // BP.
Mà \(NC \bot MD\) suy ra \(NC \bot BP\).
Vì \(SH \bot (ABCD) \Rightarrow SH \bot BP\).
Ta có \(\left\{ \begin{array}{l}BP \bot NC\\BP \bot SH\end{array} \right. \Rightarrow BP \bot (SNC) \Rightarrow (SBP) \bot (SNC)\).
Xét trong mặt phẳng (SNC), lấy E thuộc SF sao cho \(HE \bot SF\).
Ta có \(\left\{ \begin{array}{l}(SNC) \bot (SBP)\\HE \bot SF\\HE \in (SNC)\\(SNC) \cap (SBP) = SF\end{array} \right.\) suy ra \(HE \bot (SBP)\), tức \(d\left( {H,(SBP)} \right) = HE\).
Vì EP // HD và P là trung điểm của CD nên PF là đường trung bình \(\Delta DHC\), suy ra HF = CF.
Mà F thuộc (SBP) nên \(d\left( {C,(SBP)} \right) = d\left( {H,(SBP)} \right) = HE\).
Xét \(\Delta DNC\) vuông tại D, đường cao DH:
\(D{C^2} = HC.CN \Leftrightarrow HC = \frac{{D{C^2}}}{{CN}} = \frac{{D{C^2}}}{{\sqrt {D{C^2} + N{D^2}} }} = \frac{3}{{\sqrt {3 + \frac{3}{4}} }} = \frac{{2\sqrt {15} }}{5}\).
Vì F là trung điểm của CH nên \(HF = \frac{{CH}}{2} = \frac{{\sqrt {15} }}{5}\).
Xét \(\Delta SHC\) vuông tại H, đường cao HE:
\(\frac{1}{{H{E^2}}} = \frac{1}{{H{F^2}}} + \frac{1}{{S{H^2}}} = \frac{1}{{{{\left( {\frac{{\sqrt {15} }}{5}} \right)}^2}}} + \frac{1}{{{3^2}}} = \frac{{16}}{9} \Leftrightarrow HE = \frac{3}{4} = 0,75\).
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Các bài khác cùng chuyên mục
