Đề tham khảo thi THPT môn Toán - Đề số 3 (hay, chi tiết)
I. Phần trắc nghiệm
Đề bài
Nguyên hàm của hàm số \(f(x) = {3^x}\) là
-
A.
\(\frac{{{3^x}}}{{\ln 3}} + C\)
-
B.
\({3^x}\ln 3 + C\)
-
C.
\({3^x} + C\)
-
D.
\(\frac{{{3^{x + 1}}}}{{x + 1}} + C\)
Cho hàm số y = f(x) xác định và liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b được tính theo công thức
-
A.
\(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
-
B.
\(S = \int\limits_a^b {f(x)dx} \)
-
C.
\(S = - \int\limits_a^b {f(x)dx} \)
-
D.
\(S = \int\limits_b^a {\left| {f(x)} \right|dx} \)
Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là
-
A.
4,84
-
B.
2,10
-
C.
2,09
-
D.
6,94
Phương trình nào sau đây là phương trình mặt cầu (S) tâm A(2;1;0), đi qua điểm B(0;1;2)?
-
A.
\({(x + 2)^2} + {(y + 1)^2} + {z^2} = 8\)
-
B.
\({(x - 2)^2} + {(y - 1)^2} + {z^2} = 8\)
-
C.
\({(x - 2)^2} + {(y - 1)^2} + {z^2} = 64\)
-
D.
\({(x + 2)^2} + {(y + 1)^2} + {z^2} = 64\)
Cho hàm số f(x) liên tục trên mỗi khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right)\), có bảng biến thiên như hình vẽ:
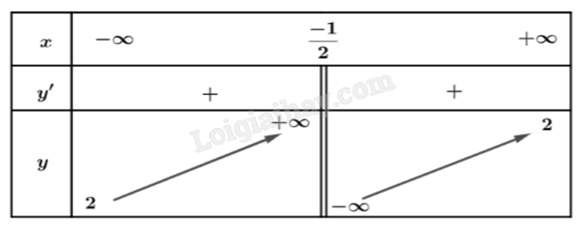
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình
-
A.
\(y = - \frac{1}{2}\)
-
B.
\(x = 2\)
-
C.
\(y = 2\)
-
D.
\(x = - \frac{1}{2}\)
Tập nghiệm của bất phương trình \({\log _5}(x - 2) \le 1\) là
-
A.
\((2;3]\)
-
B.
\(( - \infty ;7]\)
-
C.
\([7; + \infty )\)
-
D.
\((2;7]\)
Trong không gian Oxyz, cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 2t\\y = - 1\\z = 3 + t\end{array} \right.\). Đâu là tọa độ một vecto chỉ phương của đường thẳng \(\Delta \)?
-
A.
(-2;-1;1)
-
B.
(1;-1;3)
-
C.
(-2;0;1)
-
D.
(2;0;1)
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA = SB = SC = SD. Khẳng định nào sau đây đúng?
-
A.
\(SA \bot (ABCD)\)
-
B.
\(SO \bot (ABCD)\)
-
C.
\(SC \bot (ABCD)\)
-
D.
\(SB \bot (ABCD)\)
Nghiệm của phương trình \({2^x} = 3\) là
-
A.
\(x = {\log _2}3\)
-
B.
\(x = {\log _3}2\)
-
C.
\(x = \frac{3}{2}\)
-
D.
\(x = \sqrt 3 \)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = - 3\) và \({u_6} = 27\). Tính công sai d.
-
A.
7
-
B.
5
-
C.
8
-
D.
6
Cho hình hộp ABCD.EFGH.
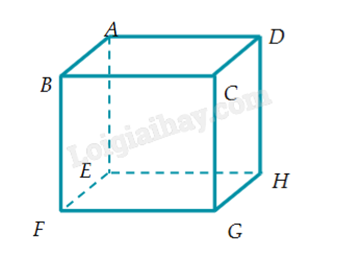
Kết quả phép toán \(\overrightarrow {AB} + \overrightarrow {EH} \) là
-
A.
\(\overrightarrow {BD} \)
-
B.
\(\overrightarrow {AE} \)
-
C.
\(\overrightarrow {EG} \)
-
D.
\(\overrightarrow {BH} \)
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ dưới đây:
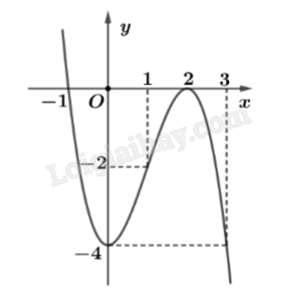
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
-
A.
\(( - 1;1)\)
-
B.
\(( - \infty ; - 1)\)
-
C.
\((2; + \infty )\)
-
D.
\((0;1)\)
Cho hàm số f(x) = x – sin2x.
a) \(f\left( 0 \right) = 0\); \(f\left( \pi \right) = \pi \).
b) Đạo hàm của hàm số đã cho là f’(x) = 1 + cos2x.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6}\) hoặc \(\frac{{5\pi }}{6}\).
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\).
Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1 m. Một ô tô A đang chạy với vận tốc 16 m/s thì gặp ô tô B đang dừng đèn đỏ nên ô tô A hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức \({v_A}(t) = 16 - 4t\) (đơn vị tính bằng m/s, thời gian t tính bằng giây).
a) Thời điểm xe ô tô A dừng lại là 4 giây kể từ lúc hãm phanh.
b) Quãng đường S(t) (đơn vị: mét) mà ô tô A đi được trong thời gian t giây \((0 \le t \le 4)\) kể từ khi hãm phanh được tính theo công thức \(S(t) = \int\limits_0^4 {v(t)dt} \).
c) Từ khi bắt đầu hãm phanh đến khi dừng lại, xe tô tô A đi được quãng đường 32 m.
d) Khoảng cách an toàn tối thiểu giữa ô tô A và ô tô B trước khi ô tô A hãm phanh là 37 m.
Một xưởng máy sử dụng một loại linh kiện được sản xuất từ hai cơ sở I và II. Số linh kiện do cơ sở I sản xuất chiếm 61%, số linh kiện do cơ sở II sản xuất chiếm 39%. Tỉ lệ linh kiện đạt tiêu chuẩn của cơ sở I, cơ sở II lần lượt là 93% và 82%. Kiểm tra ngẫu nhiên một linh kiện ở xưởng máy.
a) Xác suất linh kiện được kiểm tra do cơ sở I sản xuất là 0,61.
b) Xác suất linh kiện được kiểm tra đạt chuẩn, biết linh kiện đó do cơ sở II sản xuất là 0,82.
c) Xác suất linh kiện được kiểm tra đạt chuẩn là 0,8871.
d) Xác suất linh kiện được kiểm tra là của cơ sở I sản xuất biết linh kiện đó đạt chuẩn là 0,55.
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục toạ độ là mét), một ngọn hải đăng được đặt ở vị trí I(17;20;45). Biết rằng ngọn hải đăng đó được thiết kế với bán kính phủ sáng là 4 km.
a) Phương trình mặt cầu mô tả ranh giới bên ngoài vùng phủ sáng trên biển của hải đăng là \({(x - 17)^2} + {(y - 20)^2} + {(z - 45)^2} = 16000000\).
b) Nếu người đi biển ở vị trí M(18;21;50) thì không thể nhìn thấy ánh sáng từ ngọn hải đăng.
c) Nếu người đi biển ở vị trí N(4019;21;44) thì có thể nhìn thấy ánh sáng từ ngọn hải đăng.
d) Nếu hai người đi biển ở vị trí có thể nhìn thấy ánh sáng từ ngọn hải đăng thì khoảng cách giữa hai người đó không quá 8 km.
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\), đáy ABCD là hình chữ nhật và AD = 6. Góc giữa cạnh bên SD và mặt đáy bằng \({30^o}\). Khoảng cách giữa hai đường thẳng AB và SD bằng bao nhiêu?
Đáp án:
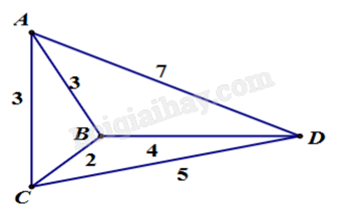
Công ty giao hàng nhanh có 4 kho hàng A, B, C và D . Quản lý muốn lên kế hoạch cho xe giao hàng đi qua tất cả các kho hàng để lấy hàng và quay lại kho hàng ban đầu, với điều kiện là mỗi kho hàng chỉ ghé qua một lần. Khoảng cách giữa các kho hàng (km) được mô tả trong hình bên. Quãng đường ngắn nhất để xe
giao hàng hoàn thành việc lấy hàng ở các kho và quay trở lại kho hàng ban đầu là bao nhiêu?
Đáp án:
Trong không gian với hệ tọa độ Oxyz, đài kiểm soát không lưu sân bay có tọa độ O(0;0;0),
mỗi đơn vị trên một trục ứng với 1 km . Máy bay bay trong phạm vi cách đài kiểm soát 417 km sẽ
hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(-688;-185;8), chuyển động theo đường
thẳng d có vectơ chỉ phương là \(\overrightarrow u = (91;75;0)\) và theo hướng về đài không lưu. E(a;b;c) là vị trí sớm nhất mà máy bay xuất hiện trên màn hình. Tính T = a + b + c.
Đáp án:
Một kiến trúc sư thiết kế một khu sinh hoạt cộng đồng có dạng hình vuông với mỗi cạnh dài 120 m. Phần sân chơi nằm ở giữa, và phần còn lại để trồng cây xanh. Các đường biên của khu vực trồng cây xanh là các đoạn parabol, với đỉnh của parabol nằm cách trung điểm của mỗi cạnh hình vuông 25 m. Tính diện tích phần trồng cây xanh.
Đáp án:
Nhà máy A chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy B . Hai nhà máy thoả thuận rằng, hàng tháng nhà máy A cung cấp cho nhà máy B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 tấn sản phẩm). Nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \(P(x) = 45 - 0,001{x^2}\) (triệu đồng). Chi phí để A sản xuất x tấn sản phẩm trong một tháng gồm 100 triệu đồng chi phí cố định và 30 triệu đồng cho mỗi tấn sản phẩm. Nhà máy A cần bán cho nhà máy B bao nhiêu tấn sản phẩm mỗi tháng để lợi nhuận thu được lớn nhất (làm tròn kết quả đến hàng phần mười)?
Đáp án:
Có hai hộp đựng bi: hộp I có 6 viên bi vàng và 4 viên bi đỏ; hộp II có 7 viên bi vàng và 3 viên bi đỏ. Chọn ngẫu nhiên một viên bi từ hộp I và chuyển nó sang hộp II. Sau đó, chọn ngẫu nhiên một viên bi từ hộp II. Tính xác suất để viên bi được chọn từ hộp II là viên bi đã được chuyển từ hộp I, biết rằng viên bi đó là viên bi vàng (làm tròn đến hàng phần trăm).
Đáp án:
Lời giải và đáp án
Nguyên hàm của hàm số \(f(x) = {3^x}\) là
-
A.
\(\frac{{{3^x}}}{{\ln 3}} + C\)
-
B.
\({3^x}\ln 3 + C\)
-
C.
\({3^x} + C\)
-
D.
\(\frac{{{3^{x + 1}}}}{{x + 1}} + C\)
Đáp án : A
Sử dụng công thức nguyên hàm của hàm số mũ: \(\int {{a^x}dx} = \frac{{{a^x}}}{{\ln a}} + C\).
\(\int {{3^x}dx} = \frac{{{3^x}}}{{\ln 3}} + C\).
Cho hàm số y = f(x) xác định và liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b được tính theo công thức
-
A.
\(S = \int\limits_a^b {\left| {f(x)} \right|dx} \)
-
B.
\(S = \int\limits_a^b {f(x)dx} \)
-
C.
\(S = - \int\limits_a^b {f(x)dx} \)
-
D.
\(S = \int\limits_b^a {\left| {f(x)} \right|dx} \)
Đáp án : A
Sử dụng công thức tính diện tích hình phẳng thông qua tích phân.
Diện tích hình phẳng giới hạn bởi y = f(x), trục hoành, x = a, x = b (a < b) là \(\int\limits_a^b {\left| {f(x)} \right|dx} \).
Điểm kiểm tra 15 phút của lớp 12A được cho bởi bảng sau:
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là
-
A.
4,84
-
B.
2,10
-
C.
2,09
-
D.
6,94
Đáp án : A
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.({u_{m + 1}} - {u_m})\).
Mẫu số liệu ghép nhóm có cỡ mẫu n = 3 + 8 + 7 + 12 + 7 + 1 + 1 = 39.
Gọi \({x_1},{x_2},...,{x_{39}}\) là điểm của 39 học sinh, giả sử dãy này đã được sắp xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{10}} \in [4;5)\).
Vậy \({Q_1} = 4 + \frac{{\frac{{39}}{4} - 3}}{8}.(5 - 4) = \frac{{155}}{{32}} \approx 4,84\).
Phương trình nào sau đây là phương trình mặt cầu (S) tâm A(2;1;0), đi qua điểm B(0;1;2)?
-
A.
\({(x + 2)^2} + {(y + 1)^2} + {z^2} = 8\)
-
B.
\({(x - 2)^2} + {(y - 1)^2} + {z^2} = 8\)
-
C.
\({(x - 2)^2} + {(y - 1)^2} + {z^2} = 64\)
-
D.
\({(x + 2)^2} + {(y + 1)^2} + {z^2} = 64\)
Đáp án : B
Mặt cầu tâm I(a;b;c) bán kính R có phương trình là \({(x - a)^2} + {(y - b)^2} + {z^2} = {R^2}\).
Bán kính của mặt cầu (S) bằng AB.
\(AB = \sqrt {{{(0 - 2)}^2} + {{(1 - 1)}^2} + {{(2 - 0)}^2}} = \sqrt 8 \).
Mặt cầu (S) tâm A(2;1;0) bán kính \(R = AB = \sqrt 8 \) có phương trình là \({(x - 2)^2} + {(y - 1)^2} + {z^2} = 8\).
Cho hàm số f(x) liên tục trên mỗi khoảng \(\left( { - \infty ; - \frac{1}{2}} \right)\) và \(\left( { - \frac{1}{2}; + \infty } \right)\), có bảng biến thiên như hình vẽ:
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình
-
A.
\(y = - \frac{1}{2}\)
-
B.
\(x = 2\)
-
C.
\(y = 2\)
-
D.
\(x = - \frac{1}{2}\)
Đáp án : C
Hàm số y = f(x) có tiệm cận ngang y = a nếu thỏa mãn ít nhất một trong những điều kiện: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = a\), \(\mathop {\lim }\limits_{x \to - \infty } f(x) = a\).
Quan sát bảng biến thiên, ta thấy \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } f(x) = 2\) nên y = 2 là đường tiệm cận ngang của đồ thị.
Tập nghiệm của bất phương trình \({\log _5}(x - 2) \le 1\) là
-
A.
\((2;3]\)
-
B.
\(( - \infty ;7]\)
-
C.
\([7; + \infty )\)
-
D.
\((2;7]\)
Đáp án : D
\(\left\{ \begin{array}{l}{\log _a}b \le m\\a > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b \le {a^m}\\b > 0\end{array} \right.\).
\({\log _5}(x - 2) \le 1 \Leftrightarrow \left\{ \begin{array}{l}x - 2 \le {5^1}\\x - 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 2 \le 5\\x > 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 7\\x > 2\end{array} \right. \Leftrightarrow 2 < x \le 7\).
Trong không gian Oxyz, cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 2t\\y = - 1\\z = 3 + t\end{array} \right.\). Đâu là tọa độ một vecto chỉ phương của đường thẳng \(\Delta \)?
-
A.
(-2;-1;1)
-
B.
(1;-1;3)
-
C.
(-2;0;1)
-
D.
(2;0;1)
Đáp án : C
Đường thẳng \(\Delta :\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) có một vecto chỉ phương là \(\overrightarrow u (a;b;c)\).
Đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 2t\\y = - 1\\z = 3 + t\end{array} \right.\) có vecto chỉ phương là \(\overrightarrow u ( - 2;0;1)\).
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA = SB = SC = SD. Khẳng định nào sau đây đúng?
-
A.
\(SA \bot (ABCD)\)
-
B.
\(SO \bot (ABCD)\)
-
C.
\(SC \bot (ABCD)\)
-
D.
\(SB \bot (ABCD)\)
Đáp án : B
Sử dụng tính chất trung điểm.
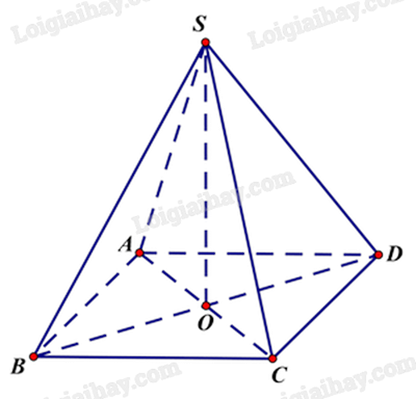
Xét tam giác SAC cân tại S có O là trung điểm của AC, suy ra SO vừa là trung truyến, vừa là đường cao của tam giác SAC.
Do đó, \(SO \bot AC\).
Chứng minh tương tự, ta được \(SO \bot BD\).
Mà AC, BD cùng thuộc mặt phẳng (ABCD) và cắt nhau tại O.
Vậy \(SO \bot (ABCD)\).
Nghiệm của phương trình \({2^x} = 3\) là
-
A.
\(x = {\log _2}3\)
-
B.
\(x = {\log _3}2\)
-
C.
\(x = \frac{3}{2}\)
-
D.
\(x = \sqrt 3 \)
Đáp án : A
\(\left\{ \begin{array}{l}{a^x} = b\\0 < a \ne 1\\b > 0\end{array} \right. \Leftrightarrow x = {\log _a}b\).
\({2^x} = 3 \Leftrightarrow x = {\log _2}3\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = - 3\) và \({u_6} = 27\). Tính công sai d.
-
A.
7
-
B.
5
-
C.
8
-
D.
6
Đáp án : D
Áp dụng công thức số hạng tổng quát của cấp số cộng: \({u_n} = {u_1} + (n - 1)d\).
\({u_6} = {u_1} + (6 - 1)d \Leftrightarrow 27 = - 3 + 5d \Leftrightarrow d = 6\).
Cho hình hộp ABCD.EFGH.
Kết quả phép toán \(\overrightarrow {AB} + \overrightarrow {EH} \) là
-
A.
\(\overrightarrow {BD} \)
-
B.
\(\overrightarrow {AE} \)
-
C.
\(\overrightarrow {EG} \)
-
D.
\(\overrightarrow {BH} \)
Đáp án : C
Áp dụng lý thuyết về hai vecto bằng nhau, quy tắc hình bình hành.
Ta có \(\overrightarrow {AB} = \overrightarrow {EF} \).
Khi đó \(\overrightarrow {EF} + \overrightarrow {EH} = \overrightarrow {EG} \) (quy tắc hình bình hành).
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ dưới đây:
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
-
A.
\(( - 1;1)\)
-
B.
\(( - \infty ; - 1)\)
-
C.
\((2; + \infty )\)
-
D.
\((0;1)\)
Đáp án : D
Hàm số đồng biến trên khoảng đồ thị đi lên từ trái sang.
Quan sát đồ thị, ta thấy đồ thị đi lên từ trái sang trong khoảng (0;2), tức hàm số đồng biến trên khoảng (0;2).
Do đó, trên khoàng (0;1), hàm số đồng biến.
Cho hàm số f(x) = x – sin2x.
a) \(f\left( 0 \right) = 0\); \(f\left( \pi \right) = \pi \).
b) Đạo hàm của hàm số đã cho là f’(x) = 1 + cos2x.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6}\) hoặc \(\frac{{5\pi }}{6}\).
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\).
a) \(f\left( 0 \right) = 0\); \(f\left( \pi \right) = \pi \).
b) Đạo hàm của hàm số đã cho là f’(x) = 1 + cos2x.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6}\) hoặc \(\frac{{5\pi }}{6}\).
d) Giá trị nhỏ nhất của f(x) trên đoạn \(\left[ {0;\pi } \right]\) là \(\frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\).
a) Thay 0, \(\pi \) vào x rồi tính giá trị biểu thức.
b) Áp dụng công thức đạo hàm của hàm hợp lượng giác: (sinu)’ = u’.cosu.
c) Nếu \(\cos \alpha = m\) thì \(\cos x = m \Leftrightarrow \cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
Dựa vào khoảng hoặc đoạn đề bài cho, tìm các giá trị k thỏa mãn rồi thay vào công thức nghiệm và kết luận.
d) Thay giá trị hai đầu mút của đoạn và các giá trị sao cho f’(x) = 0 vào f(x) và tìm giá trị nhỏ nhất.
a) Đúng. \(f\left( 0 \right) = 0 - \sin (2.0) = 0\) và \(f\left( \pi \right) = \pi - \sin (2\pi ) = \pi \).
b) Sai. f’(x) = 1 – 2cos2x.
c) Đúng. \(1 - 2\cos 2x = 0 \Leftrightarrow \cos 2x = \frac{1}{2} \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{3} + k2\pi \\2x = - \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{6} + k\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
+) \(0 \le x \le \pi \Leftrightarrow 0 \le \frac{\pi }{6} + k\pi \le \pi \Leftrightarrow - \frac{\pi }{6} \le k\pi \le \frac{{5\pi }}{6} \Leftrightarrow - \frac{1}{6} \le k \le \frac{5}{6} \Rightarrow k = 0\) (vì \(k \in \mathbb{Z}\)).
Suy ra \(x = \frac{\pi }{6} + 0.\pi = \frac{\pi }{6}\).
+) \(0 \le x \le \pi \Rightarrow 0 \le - \frac{\pi }{6} + k\pi \le \pi \Leftrightarrow \frac{\pi }{6} \le k\pi \le \frac{{7\pi }}{6} \Leftrightarrow \frac{1}{6} \le k \le \frac{7}{6} \Rightarrow k = 1\) (vì \(k \in \mathbb{Z}\)).
Suy ra \(x = - \frac{\pi }{6} + 1.\pi = \frac{{5\pi }}{6}\).
Vậy trên đoạn \(\left[ {0;\pi } \right]\) thì f’(x) = 0 có hai nghiệm là \(x = \frac{\pi }{6}\); \(x = \frac{{5\pi }}{6}\).
d) Đúng. f(x) = sin2x – x;
f’(x) = 2cos2x – 1 có nghiệm \(x = \frac{\pi }{6}\); \(x = \frac{{5\pi }}{6}\) thuộc \(\left[ {0;\pi } \right]\).
\(f\left( 0 \right) = 0\); \(f\left( \pi \right) = \pi \); \(f\left( {\frac{\pi }{6}} \right) = \frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\); \(f\left( {\frac{{5\pi }}{6}} \right) = \frac{{5\pi }}{6} + \frac{{\sqrt 3 }}{2}\).
Vậy giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) là \(\frac{\pi }{6} - \frac{{\sqrt 3 }}{2}\).
Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1 m. Một ô tô A đang chạy với vận tốc 16 m/s thì gặp ô tô B đang dừng đèn đỏ nên ô tô A hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức \({v_A}(t) = 16 - 4t\) (đơn vị tính bằng m/s, thời gian t tính bằng giây).
a) Thời điểm xe ô tô A dừng lại là 4 giây kể từ lúc hãm phanh.
b) Quãng đường S(t) (đơn vị: mét) mà ô tô A đi được trong thời gian t giây \((0 \le t \le 4)\) kể từ khi hãm phanh được tính theo công thức \(S(t) = \int\limits_0^4 {v(t)dt} \).
c) Từ khi bắt đầu hãm phanh đến khi dừng lại, xe tô tô A đi được quãng đường 32 m.
d) Khoảng cách an toàn tối thiểu giữa ô tô A và ô tô B trước khi ô tô A hãm phanh là 37 m.
a) Thời điểm xe ô tô A dừng lại là 4 giây kể từ lúc hãm phanh.
b) Quãng đường S(t) (đơn vị: mét) mà ô tô A đi được trong thời gian t giây \((0 \le t \le 4)\) kể từ khi hãm phanh được tính theo công thức \(S(t) = \int\limits_0^4 {v(t)dt} \).
c) Từ khi bắt đầu hãm phanh đến khi dừng lại, xe tô tô A đi được quãng đường 32 m.
d) Khoảng cách an toàn tối thiểu giữa ô tô A và ô tô B trước khi ô tô A hãm phanh là 37 m.
a) Khi xe ô tô dừng hẳn thì \({v_A}(t) = 0\). Giải phương trình tìm t.
b, c) Sử dụng công thức \(S(t) = \int\limits_0^t {v(t)dt} \).
d) Khoảng cách an toàn tối thiểu giữa ô tô A và ô tô B trước khi ô tô A hãm phanh bằng tổng quãng đường ô tô A di chuyển từ lúc hãm phanh đến khi dừng hẳn và khoảng cách tối thiểu khi dừng đèn đỏ.
a) Đúng. Khi ô tô A dừng lại thì \({v_A}(t) = 0 \Leftrightarrow 16 - 4t = 0 \Leftrightarrow t = 4\).
b) Sai. Quãng đường S(t) ô tô đi được trong thời gian t giây \((0 \le t \le 4)\) được tính theo công thức \(S(t) = \int\limits_0^t {v(t)dt} \).
c) Đúng. Quãng đường xe tô tô A đi được kể từ lúc hãm phanh đến khi dừng hẳn là \(S(t) = \int\limits_0^4 {(16 - 4t)dt} = 32\) (m).
d) Sai. Để đảm bảo khoảng cách an toàn tối thiểu 1 m khi dừng lại, ô tô A phải bắt đầu hãm phanh khi cách ô tô B ít nhất 32 + 1 = 33 (m).
Một xưởng máy sử dụng một loại linh kiện được sản xuất từ hai cơ sở I và II. Số linh kiện do cơ sở I sản xuất chiếm 61%, số linh kiện do cơ sở II sản xuất chiếm 39%. Tỉ lệ linh kiện đạt tiêu chuẩn của cơ sở I, cơ sở II lần lượt là 93% và 82%. Kiểm tra ngẫu nhiên một linh kiện ở xưởng máy.
a) Xác suất linh kiện được kiểm tra do cơ sở I sản xuất là 0,61.
b) Xác suất linh kiện được kiểm tra đạt chuẩn, biết linh kiện đó do cơ sở II sản xuất là 0,82.
c) Xác suất linh kiện được kiểm tra đạt chuẩn là 0,8871.
d) Xác suất linh kiện được kiểm tra là của cơ sở I sản xuất biết linh kiện đó đạt chuẩn là 0,55.
a) Xác suất linh kiện được kiểm tra do cơ sở I sản xuất là 0,61.
b) Xác suất linh kiện được kiểm tra đạt chuẩn, biết linh kiện đó do cơ sở II sản xuất là 0,82.
c) Xác suất linh kiện được kiểm tra đạt chuẩn là 0,8871.
d) Xác suất linh kiện được kiểm tra là của cơ sở I sản xuất biết linh kiện đó đạt chuẩn là 0,55.
a, b) Dựa vào số liệu đề bài cho.
c) Áp dụng công thức xác suất toàn phần.
d) Áp dụng công thức Bayes.
Gọi:
\({A_1}\): “Linh kiện được kiểm tra do cơ sở I sản xuất”.
\({A_2}\): “Linh kiện được kiểm tra do cơ sở II sản xuất”.
B: “Linh kiện được kiểm tra đạt chuẩn”.
a) Đúng. \(P({A_1}) = 61\% = 0,61\).
b) Đúng. \(P(B|{A_2}) = 82\% = 0,82\).
c) Đúng. Vì \({A_1}\), \({A_2}\) là một hệ biến cố đầy đủ nên theo công thức xác suất toàn phần, ta có:
\(P(B) = P({A_1}).P(B|{A_1}) + P({A_2}).P(B|{A_2}) = 0,61.0,93 + 0,39.0,82 = 0,8871\).
d) Sai. Theo công thức Bayes, ta có: \(P({A_1}|B) = \frac{{P({A_1}).P(B|{A_1})}}{{P(B)}} = \frac{{0,61.0,93}}{{0,8871}} \approx 0,64\).
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục toạ độ là mét), một ngọn hải đăng được đặt ở vị trí I(17;20;45). Biết rằng ngọn hải đăng đó được thiết kế với bán kính phủ sáng là 4 km.
a) Phương trình mặt cầu mô tả ranh giới bên ngoài vùng phủ sáng trên biển của hải đăng là \({(x - 17)^2} + {(y - 20)^2} + {(z - 45)^2} = 16000000\).
b) Nếu người đi biển ở vị trí M(18;21;50) thì không thể nhìn thấy ánh sáng từ ngọn hải đăng.
c) Nếu người đi biển ở vị trí N(4019;21;44) thì có thể nhìn thấy ánh sáng từ ngọn hải đăng.
d) Nếu hai người đi biển ở vị trí có thể nhìn thấy ánh sáng từ ngọn hải đăng thì khoảng cách giữa hai người đó không quá 8 km.
a) Phương trình mặt cầu mô tả ranh giới bên ngoài vùng phủ sáng trên biển của hải đăng là \({(x - 17)^2} + {(y - 20)^2} + {(z - 45)^2} = 16000000\).
b) Nếu người đi biển ở vị trí M(18;21;50) thì không thể nhìn thấy ánh sáng từ ngọn hải đăng.
c) Nếu người đi biển ở vị trí N(4019;21;44) thì có thể nhìn thấy ánh sáng từ ngọn hải đăng.
d) Nếu hai người đi biển ở vị trí có thể nhìn thấy ánh sáng từ ngọn hải đăng thì khoảng cách giữa hai người đó không quá 8 km.
a) Phương trình mặt cầu tâm I(a;b;c), bán kính R là \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\).
b, c) Tính khoảng cách giữa người đó và ngọn hải đăng và so sánh với bán kính phủ sáng.
d) So sánh khoảng cách giữa hai người với đường kính phủ sáng.
a) Đúng. Phương trình mặt cầu mô tả ranh giới bên ngoài vùng phủ sáng trên biển của hải đăng là phương trình mặt cầu tâm I(17;20;45), bán kính 4000 m: \({(x - 17)^2} + {(y - 20)^2} + {(z - 45)^2} = 16000000\).
b) Sai. \(IM = \sqrt {{{(18 - 17)}^2} + {{(21 - 20)}^2} + {{(50 - 45)}^2}} = \sqrt {27} < 16000000\). Khi đó, người ở vị trí điểm M có thể nhìn thấy ánh sáng từ ngọn hải đăng.
c) Sai. \(IN = \sqrt {{{(4019 - 17)}^2} + {{(21 - 20)}^2} + {{(44 - 45)}^2}} = \sqrt {16016006} > 16000000\). Khi đó, người ở vị trí điểm N không thể nhìn thấy ánh sáng từ ngọn hải đăng.
d) Đúng. Vì đường kính của mặt cầu trên bằng 8000 m hay 8 km nên khoảng cách giữa hai người đi biển ở vị trí có thể nhìn thấy ánh sáng từ ngọn hải đăng không quá 8 km.
Cho hình chóp S.ABCD có \(SA \bot (ABCD)\), đáy ABCD là hình chữ nhật và AD = 6. Góc giữa cạnh bên SD và mặt đáy bằng \({30^o}\). Khoảng cách giữa hai đường thẳng AB và SD bằng bao nhiêu?
Đáp án:
Đáp án:
Tìm đoạn vuông góc chung của AB và SD và tính độ dài đoạn thẳng đó.
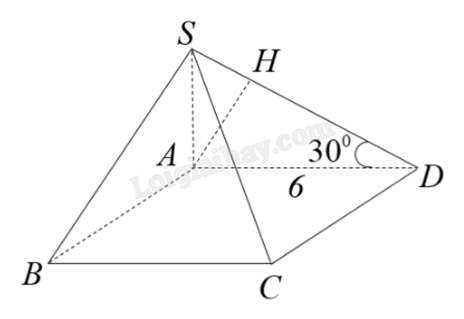
Trong mặt phẳng (SAD), kẻ \(AH \bot DA = \{ H\} \).
Ta có \(\left\{ \begin{array}{l}SA \bot (ABCD) \Rightarrow SA \bot AB\\AD \bot AB\end{array} \right.\) suy ra \(AB \bot (SAD)\), mà \(AH \subset (SAD)\) nên \(AB \bot AH\).
Khi đó, AH là đoạn vuông góc chung của AB và SD.
Xét tam giác SAD vuông tại A, có
\(\tan \widehat {SDA} = \frac{{SA}}{{AD}} \Leftrightarrow SA = AD\tan \widehat {SDA} = 6\tan {30^o} = 2\sqrt 3 \).
Xét tam giác SAD vuông tại A có đường cao AH:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} \Leftrightarrow AH = \frac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{{2\sqrt 3 .6}}{{\sqrt {{{\left( {2\sqrt 3 } \right)}^2} + {6^2}} }} = 3\).
Công ty giao hàng nhanh có 4 kho hàng A, B, C và D . Quản lý muốn lên kế hoạch cho xe giao hàng đi qua tất cả các kho hàng để lấy hàng và quay lại kho hàng ban đầu, với điều kiện là mỗi kho hàng chỉ ghé qua một lần. Khoảng cách giữa các kho hàng (km) được mô tả trong hình bên. Quãng đường ngắn nhất để xe
giao hàng hoàn thành việc lấy hàng ở các kho và quay trở lại kho hàng ban đầu là bao nhiêu?
Đáp án:
Đáp án:
Liệt kê và so sánh.
Xe giao hàng có thể xuất phát từ một trong 4 kho hàng A, B, C, D.
Giả sử xe giao hàng xuất phát từ kho A.
Để đi qua tất cả các kho hàng và quay trở về A , xe giao hàng có thể đi theo một trong các đường đi:
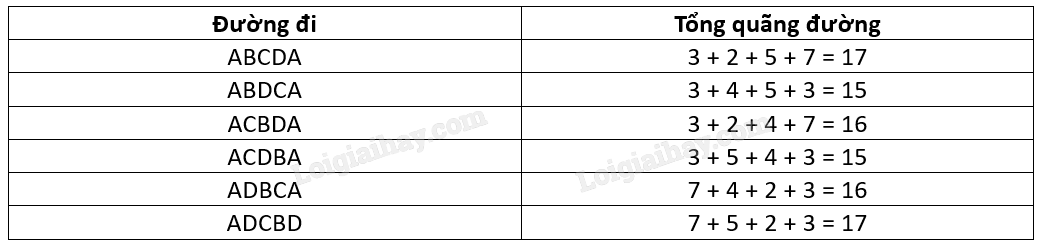
Nếu xuất phát từ đỉnh khác thì chỉ là phép thay thế bước đi trong sơ đồ trên.
Vậy quãng đường ngắn nhất để xe giao hàng hoàn thành việc lấy hàng ở các kho và quay trở lại
kho hàng ban đầu là 15 km.
Trong không gian với hệ tọa độ Oxyz, đài kiểm soát không lưu sân bay có tọa độ O(0;0;0),
mỗi đơn vị trên một trục ứng với 1 km . Máy bay bay trong phạm vi cách đài kiểm soát 417 km sẽ
hiển thị trên màn hình ra đa. Một máy bay đang ở vị trí A(-688;-185;8), chuyển động theo đường
thẳng d có vectơ chỉ phương là \(\overrightarrow u = (91;75;0)\) và theo hướng về đài không lưu. E(a;b;c) là vị trí sớm nhất mà máy bay xuất hiện trên màn hình. Tính T = a + b + c.
Đáp án:
Đáp án:
Tìm tọa độ điểm E theo tham số. Dựa vào khoảng cách OE tìm giá trị của tham số, từ đó kết luận tọa độ điểm E.
Phương trình chuyển động của máy bay là phương trình đường thẳng đi qua A(-688;-185;8) và có vecto chỉ phương là \(\overrightarrow u = (91;75;0)\): \(\left\{ \begin{array}{l}x = - 688 + 91t\\y = - 185 + 75t\\z = 8\end{array} \right.\) (\(t \ge 0\) vì máy bay đang hướng về đài không lưu – gốc tọa độ O, mà tọa độ x, y của máy bay đang có giá trị âm).
Điểm E nằm trên đường chuyển động của máy bay nên \(E( - 688 + 91{t_E}; - 185 + 75{t_E};8)\).
Mà E là vị trí sớm nhất máy bay xuất hiện trên màn hình ra đa nên E cách O đúng 417 km.
Suy ra \(OE = 471 \Leftrightarrow {( - 688 + 91t)^2} + {( - 185 + 75t)^2} + {8^2} = {417^2} \Leftrightarrow 13906{t^2} - 152966t + 333744 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = 8\end{array} \right.\).
Vì E là vị trí sớm nhất mà máy bay xuất hiện trên màn hình nên t = 3. Khi đó E(-415;40;8).
Vậy a + b + c = -415 + 40 + 8 = -367.
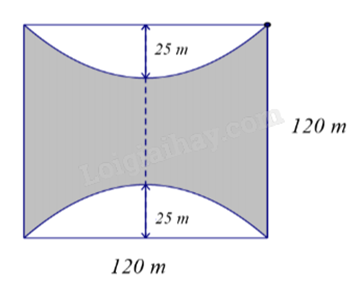
Một kiến trúc sư thiết kế một khu sinh hoạt cộng đồng có dạng hình vuông với mỗi cạnh dài 120 m. Phần sân chơi nằm ở giữa, và phần còn lại để trồng cây xanh. Các đường biên của khu vực trồng cây xanh là các đoạn parabol, với đỉnh của parabol nằm cách trung điểm của mỗi cạnh hình vuông 25 m. Tính diện tích phần trồng cây xanh.
Đáp án:
Đáp án:
Chọn hệ trục tọa độ phù hợp, từ đó tìm ra hàm số có đồ thị giới hạn phần diện tích cần tìm. Tính diện tích bằng cách sử dụng tích phân.
Chọn hệ trục tọa độ Oxy như hình vẽ:
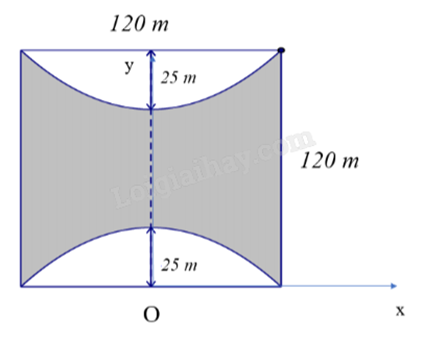
Giả sử parabol (P) có bề lõm hướng xuống dưới có phương trình là \(y = a{x^2} + bx + c\) \((a \ne 0)\).
(P) đi qua ba điểm (0;25), (-60;0) và (60;0) nên ta có:
\(\left\{ \begin{array}{l}25 = a{.0^2} + b.0 + c\\0 = a{.60^2} + b.60 + c\\0 = a.{( - 60)^2} + b.( - 60) + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{{144}}\\b = 0\\c = 25\end{array} \right.\).
Vậy (P): \(y = - \frac{1}{{144}}{x^2} + 25\).
Diện tích của phần trồng cây xanh là \(2\int\limits_{ - 60}^{60} {\left| { - \frac{1}{{144}}{x^2} + 25} \right|dx} = 2\int\limits_{ - 60}^{60} {\left( { - \frac{1}{{144}}{x^2} + 25} \right)dx} = 4000\) \(({m^2})\).
Nhà máy A chuyên sản xuất một loại sản phẩm cung cấp cho nhà máy B . Hai nhà máy thoả thuận rằng, hàng tháng nhà máy A cung cấp cho nhà máy B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 tấn sản phẩm). Nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \(P(x) = 45 - 0,001{x^2}\) (triệu đồng). Chi phí để A sản xuất x tấn sản phẩm trong một tháng gồm 100 triệu đồng chi phí cố định và 30 triệu đồng cho mỗi tấn sản phẩm. Nhà máy A cần bán cho nhà máy B bao nhiêu tấn sản phẩm mỗi tháng để lợi nhuận thu được lớn nhất (làm tròn kết quả đến hàng phần mười)?
Đáp án:
Đáp án:
Lập hàm số tính lợi nhuận theo x và tìm x để hàm số đạt giá trị lớn nhất.
Số tiền nhà máy A thu được từ việc bán x tấn sản phẩm \((0 \le x \le 100)\) cho nhà máy B là:
\(R(x) = x.P(x) = x(45 - 0,001{x^2}) = 45x - 0,001{x^3}\) (triệu đồng).
Chi phí để A sản xuất x tấn sản phẩm trong một tháng là C(x) = 100 + 30x (triệu đồng).
Lợi nhuận (triệu đồng) mà nhà máy A thu được là:
\(P(x) = R(x) - C(x) = 45x - 0,001{x^3} - (100 + 30x) = - 0,001{x^3} + 15x - 100\) (triệu đồng).
Xét hàm số \(P(x) = - 0,001{x^3} + 15x - 100\) với \(0 \le x \le 100\), ta có:
\(P'(x) = - 0,003{x^2} + 15 = 0 \Leftrightarrow {x^2} = 5000 \Leftrightarrow x = 50\sqrt 2 \).
Ta có bảng biến thiên:
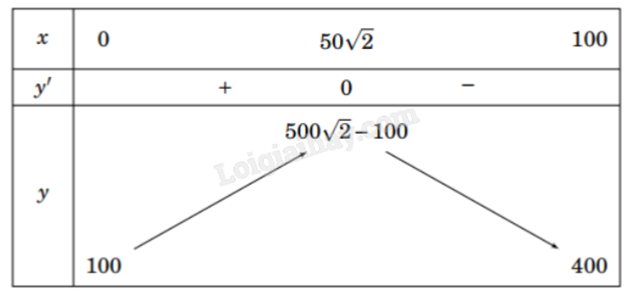
Vậy nhà máy A thu được lợi nhuận lớn nhất khi bán tấn sản phẩm cho nhà máy B mỗi tháng.
Có hai hộp đựng bi: hộp I có 6 viên bi vàng và 4 viên bi đỏ; hộp II có 7 viên bi vàng và 3 viên bi đỏ. Chọn ngẫu nhiên một viên bi từ hộp I và chuyển nó sang hộp II. Sau đó, chọn ngẫu nhiên một viên bi từ hộp II. Tính xác suất để viên bi được chọn từ hộp II là viên bi đã được chuyển từ hộp I, biết rằng viên bi đó là viên bi vàng (làm tròn đến hàng phần trăm).
Đáp án:
Đáp án:
Sử dụng công thức xác suất có điều kiện.
A: “Viên bi được chọn từ hộp II là viên bi được chuyển từ hộp I”.
B: “Viên bi được chọn từ hộp II là viên bi vàng”.
A và B là hai biến cố độc lập nên P(AB) = P(A).P(B).
Xác suất để viên bi được chọn từ hộp II là viên bi đã được chuyển từ hộp I, biết rằng viên bi đó là viên bi vàng là \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\). Ta cần tính P(AB) và P(B).
* Tính P(B):
TH1: Chuyển một viên bi vàng từ hộp I sang hộp II:
Xác suất chọn viên bi vàng từ hộp I là \(\frac{6}{{10}}\).
Khi chuyển một viên bi vàng từ hộp I, số viên vàng trong hộp II sẽ là 8 trong số 11 viên. Xác suất để chọn một viên bi vàng từ hộp II khi đó là \(\frac{6}{{10}}.\frac{8}{{11}}\).
TH2: Chuyển một viên bi đỏ từ hộp I sang hộp II:
Xác suất chọn viên bi đỏ từ hộp I là \(\frac{4}{{10}}\).
Khi chuyển một viên bi đỏ từ hộp I, số viên vàng trong hộp II vẫn là 7 trong số 11 viên. Xác suất để chọn một viên bi vàng từ hộp II khi đó là \(\frac{4}{{10}}.\frac{7}{{11}}\).
Vậy \(P(B) = \frac{6}{{10}}.\frac{8}{{11}} + \frac{4}{{10}}.\frac{7}{{11}} = \frac{{76}}{{110}}\).
* Tính P(AB):
Để lấy đúng viên bi vàng vừa được chuyển từ hộp I cần có 2 giai đoạn:
- Xác suất chọn được bi vàng từ hộp I: \(\frac{6}{{10}}\).
- Xác suất chọn được viên bi vừa được lấy từ hộp I: \(\frac{1}{{11}}\).
Vậy \(P(AB) = \frac{6}{{10}}.\frac{1}{{11}} = \frac{6}{{110}}\).
* Tính \(P(A|B) = \frac{{P(AB)}}{{P(B)}}\):
\(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{\frac{6}{{110}}}}{{\frac{{76}}{{110}}}} = \frac{6}{{76}} \approx 0,08\).
Các bài khác cùng chuyên mục
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Ninh Bình
- Đề thi thử THPT môn Toán năm 2025 Sở GD Hà Tĩnh
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Vĩnh Phúc
- Đề tham khảo thi THPT môn Toán - Đề số 3 (hay, chi tiết)
- Đề tham khảo thi THPT môn Toán - Đề số 2 (hay, chi tiết)
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Ninh Bình
- Đề thi thử THPT môn Toán năm 2025 Sở GD Hà Tĩnh
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Vĩnh Phúc
- Đề tham khảo thi THPT môn Toán - Đề số 3 (hay, chi tiết)
- Đề tham khảo thi THPT môn Toán - Đề số 2 (hay, chi tiết)
