-
Đề thi chính thức tốt nghiệp THPT môn Toán
-
Đề thi thử tốt nghiệp THPT môn Toán
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Vĩnh Phúc
- Đề thi thử tốt nghiệp THPT môn Toán năm 2025 Sở GD Hà Tĩnh
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Ninh Bình
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 3 - Thanh Hóa
- Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2025 cụm các trường số 4 - Hải Dương
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Phú Thọ
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 4 - Thanh Hóa
- Đề thi thử tốt nghiệp THPT môn Toán năm 2025 Sở GD Quảng Bình
- Đề KSCL Toán 11 năm 2024 - 2025 sở GD&ĐT Hà Nội
- Đề KSCL Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội
-
Đề tham khảo thi tốt nghiệp THPT môn Toán
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 1
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 2
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 3
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 4
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 5
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 6
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 7
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 8
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 9
Đề tham khảo thi THPT môn Toán - Đề số 6 (hay, chi tiết)
I. Phần trắc nghiệm
Đề bài
Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm \(M\left( {2;0; - 1} \right)\) và có vecto chỉ phương \(\overrightarrow a = \left( {2; - 3;1} \right)\) là
-
A.
\(\left\{ \begin{array}{l}x = 4 + 2t\\y = - \,6\\z = 2 - t\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = - \,3t\\z = - 1 + t\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - \,3t\\z = 1 + t\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = - 2 + 4t\\y = - \,6t\\z = 1 + 2t\end{array} \right.\)
Tính tích phân \(I = \int\limits_{ - 1}^0 {\left( {2x + 1} \right)dx} \).
-
A.
I = 0
-
B.
I = 1
-
C.
I = 2
-
D.
I = \( - \frac{1}{2}\)
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 4}}{{x - 1}}\) là đường thẳng
-
A.
x = 2
-
B.
x = 1
-
C.
y = 2
-
D.
y = 1
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_4} = 54\). Công bội của cấp số nhân này bằng
-
A.
\(\frac{{52}}{3}\)
-
B.
-3
-
C.
\( - \frac{{52}}{3}\)
-
D.
3
Cho tập hợp A = {0;1;2;3;4;5}. Có bao nhiêu số tự nhiên có 4 chữ số và các chữ số thuộc A?
-
A.
1296
-
B.
300
-
C.
1080
-
D.
360
Cho mẫu số liệu ghép nhóm với bộ ba tứ phân vị lần lượt là \({Q_1} = 11,5\); \({Q_2} = 14,5\); \({Q_3} = 21,3.\) Khi đó khoảng tứ phân vị của mẫu số liệu trên là
-
A.
\(\Delta Q = 3,0\)
-
B.
\(\Delta Q = 6,8\)
-
C.
\(\Delta Q = 9,8\)
-
D.
\(\Delta Q = 32,8\)
Nghiệm của phương trình \({3^{{x^2} - 3x + 4}} = 9\) là
-
A.
x = 1; x = 2
-
B.
x = -1; x = 3
-
C.
x = 1; x = -2
-
D.
x = -1; x = 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, đường thẳng SA vuông góc với mặt phẳng (ABCD) và SA = 3a. Thể tích của khối chóp S.ABCD bằng
-
A.
\(2{a^3}\)
-
B.
\(3{a^3}\)
-
C.
\(6{a^3}\)
-
D.
\({a^3}\)
v
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = \left( {1; - 2;1} \right)\) và \(\overrightarrow b = \left( {2; - 4; - 2} \right)\). Khi đó \(\overrightarrow a .\overrightarrow b \) bằng
-
A.
8
-
B.
-8
-
C.
12
-
D.
-12
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau:
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
-
A.
[7;9)
-
B.
[9;11)
-
C.
[11;13)
-
D.
[13;15)
Trong không gian với Oxyz, cho hai điểm A(1;2;3), B(-2;-4;9). Điểm M thuộc đoạn thẳng AB sao cho MA = 2MB. Độ dài đoạn thẳng OM là
-
A.
5
-
B.
3
-
C.
\(\sqrt {17} \)
-
D.
\(3\sqrt 6 \)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-2;7), B(-3;8;-1). Mặt cầu đường kính AB có phương trình là
-
A.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 3} \right)^2} = \sqrt {45} \)
-
B.
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 3} \right)^2} = 45\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 3} \right)^2} = \sqrt {45} \)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 3} \right)^2} = 45\)
Một huấn luyện viên môn bóng rổ thống kê lại số quả bóng được ném vào rổ của một nhóm vận động viên đang tập luyện mỗi người ném 11 lần như sau:
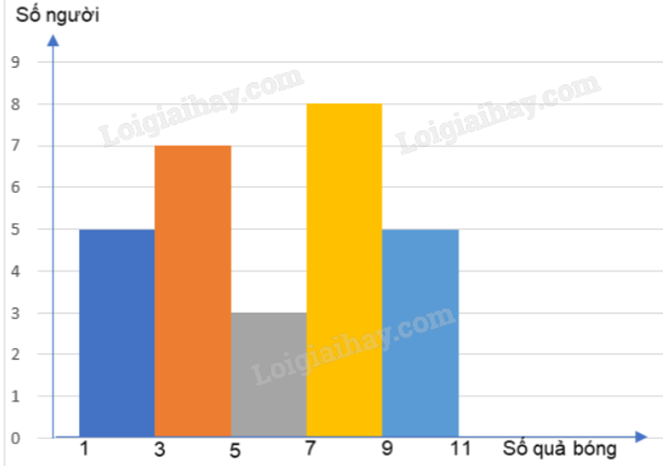
a) Từ biểu đồ, có thể lập được bảng tần số ghép nhóm gồm 5 nhóm biết mỗi nhóm có độ dài là 2.
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên lớn hơn 5.
c) Số trung bình của mẫu số liệu bằng \(\frac{{85}}{{14}}\).
d) Độ lệch chuẩn của mẫu số liệu trên lớn hơn 3.
Cho hình chóp S.ABC có mặt bên (SAB) vuông góc với mặt đáy và tam giác đều SAB cạnh 2a. Biết tam giác ABC vuông tại C và cạnh \(AC = a\sqrt 3 \).
a) \(SH \bot (ABC)\) với H là trung điểm AB.
b) \(d\left( {S,(ABC)} \right) = a\sqrt 3 \).
c) \(d\left( {C,(SAB)} \right) = \frac{{a\sqrt 3 }}{3}\).
d) Thể tích của khối chóp S.ABC bằng \(\frac{{{a^3}}}{6}\).
Cho một cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu bằng -7, số hạng thứ hai bằng 14 và số hạng cuối bằng 14336.
a) Công bội của cấp số nhân bằng 2.
b) 224 là số hạng thứ năm của cấp số nhân đã cho.
c) Cấp số nhân đã cho có 12 số hạng.
d) Tổng \({u_1} + {u_3} + {u_5} + {u_7} + {u_9}\) bằng -2387.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình x – y – z – 3 = 0 và hai điểm A(1;-3;-4), B(1;2;1).
a) Mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n = (1; - 1; - 1)\).
b) \(\overrightarrow {AB} = (0;5;5)\).
c) Khoảng cách từ điểm A đến (P) là \(\frac{{5\sqrt 3 }}{3}\).
d) Cho điểm M di động trên (P). Khi đó giá trị nhỏ nhất của biểu thức \(M{A^2} + M{B^2}\) bằng 56.
Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy dài 2,4 m và độ dài các cạnh bên của hình chóp bằng 3 m . Gọi góc nhị diện giữa hai mặt bên đối diện của mái che giếng trời đó là \(\alpha \), tính \(\cos \alpha \) (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Một bình đựng 30 viên bi kích thước, chất liệu như nhau, trong đó có 20 viên bi xanh và 10 viên bi trắng. Lấy ngẫu nhiên ra một viên bi, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được một viên bi xanh ở lần thứ nhất và một viên bi trắng ở lần thứ hai (làm tròn kết quả đến hàng phần trăm).
Đáp án:
Một người điều khiển một flycam để phục vụ trong một chương trình của đài truyền hình. Đầu tiên flycam ở vị trí A cách vị trí điều khiển 100 m về phía nam và 150 m về phía đông, đồng thời cách mặt đất 30 m. Để thực hiện nhiệm vụ tiếp theo, người đó điều khiển flycam đến vị trí B cách vị trí điều khiển 100 m về phía bắc và 50 m về phía tây, đồng thời cách mặt đất 40 m. Biết flycam bay theo một đường thẳng từ vị trí A đến vị trí B tạo thành một vecto \(\overrightarrow {AB} \). Tính \(\left| {\overrightarrow {AB} } \right|\) (kết quả làm tròn đến hàng đơn vị của mét).
Đáp án:
Trong 10 giây đầu tiên, một chất điểm chuyển động theo phương trình \(s(t) = {t^3} - 12{t^2} + 5t + 1\), trong đó thời gian t được tính bằng giây, quãng đường s tính bằng mét. Hỏi sau khoảng thời gian bao nhiêu giây thì vận tốc tức thời của chất điểm bắt đầu tăng lên?
Đáp án:
Từ một tấm bìa mỏng hình vuông cạnh 6 dm, bạn Hoa cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy là cạnh của hình vuông ban đầu và đỉnh là đỉnh của một hình vuông nhỏ phía trong rồi gập lên, ghép lại tạo thành một khối chóp tứ giác đều (hình vẽ sau).
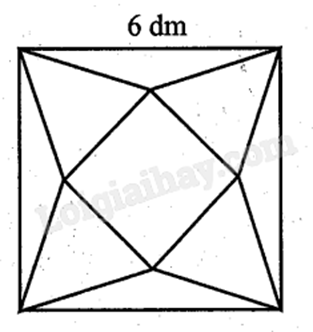
Thể tích của khối chóp có giá trị lớn nhất bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng phần mười)?
Đáp án:
Cho đường thẳng \(y = \frac{3}{4}x\) và parabol \(y = \frac{1}{2}{x^2} + a\), (\(a\) là tham số thực dương). Gọi \({S_1}\), \({S_2}\) lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi \({S_1} = {S_2}\) thì giá trị biểu thức 128a + 3 bằng bao nhiêu?
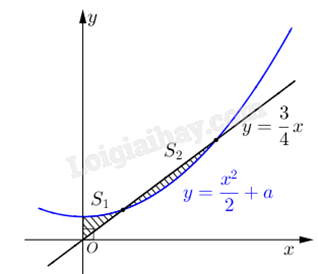
Đáp án:
Lời giải và đáp án
Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm \(M\left( {2;0; - 1} \right)\) và có vecto chỉ phương \(\overrightarrow a = \left( {2; - 3;1} \right)\) là
-
A.
\(\left\{ \begin{array}{l}x = 4 + 2t\\y = - \,6\\z = 2 - t\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x = 2 + 2t\\y = - \,3t\\z = - 1 + t\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - \,3t\\z = 1 + t\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = - 2 + 4t\\y = - \,6t\\z = 1 + 2t\end{array} \right.\)
Đáp án : B
Theo lý thuyết về đường thẳng trong không gian Oxyz, ta có phương trình tham số của đường thẳng đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có vecto chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\) là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \(\left( {t \in \mathbb{R}} \right)\).
Phương trình tham số của đường thẳng đi qua điểm \(M\left( {2;0; - 1} \right)\) và có vecto chỉ phương \(\overrightarrow a = \left( {2; - 3;1} \right)\) là \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - \,3t\\z = - 1 + t\end{array} \right.\) \(\left( {t \in \mathbb{R}} \right)\).
Tính tích phân \(I = \int\limits_{ - 1}^0 {\left( {2x + 1} \right)dx} \).
-
A.
I = 0
-
B.
I = 1
-
C.
I = 2
-
D.
I = \( - \frac{1}{2}\)
Đáp án : A
Áp dụng công thức tính tích phân của hàm số lũy thừa \(\int\limits_a^b {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right.\).
\(I = \int\limits_{ - 1}^0 {\left( {2x + 1} \right)dx} = \left. {\left( {{x^2} + x} \right)} \right|_{ - 1}^0 = \left( {{0^2} + 0} \right) - \left( {{{\left( { - 1} \right)}^2} - 1} \right) = 0\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{2x + 4}}{{x - 1}}\) là đường thẳng
-
A.
x = 2
-
B.
x = 1
-
C.
y = 2
-
D.
y = 1
Đáp án : C
Đồ thị hàm số y = f(x) có đường tiệm cận ngang là \(y = {y_0}\) nếu thõa mãn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f(x) = {y_0}\).
Ta có \(\mathop {\lim }\limits_{x \to \pm \infty } \frac{{2x + 4}}{{x - 1}} = 2\) nên đồ thị hàm số có đường tiệm cận ngang là y = 2.
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_4} = 54\). Công bội của cấp số nhân này bằng
-
A.
\(\frac{{52}}{3}\)
-
B.
-3
-
C.
\( - \frac{{52}}{3}\)
-
D.
3
Đáp án : D
Áp dụng công thức số hạng tổng quát của cấp số nhân \({u_n} = {u_1}.{q^{n - 1}}\).
Gọi q là công bội của cấp số nhân \(\left( {{u_n}} \right)\).
Ta có: \({u_4} = {u_1}\,.\,{q^3} \Leftrightarrow 54 = 2\,.\,{q^3} \Leftrightarrow {q^3} = 27 \Leftrightarrow q = 3\).
Cho tập hợp A = {0;1;2;3;4;5}. Có bao nhiêu số tự nhiên có 4 chữ số và các chữ số thuộc A?
-
A.
1296
-
B.
300
-
C.
1080
-
D.
360
Đáp án : C
Áp dụng quy tắc nhân.
Gọi số có 4 chữ số thỏa yêu cầu bài toán có dạng là: \(\overline {{a_1}{a_2}{a_3}{a_4}} \).
Số cách chọn \({a_1}\) là 5 (trừ chữ số 0).
Số cách chọn \({a_2}\) là 6.
Số cách chọn \({a_3}\) là 6.
Số cách chọn \({a_4}\) là 6.
Vậy theo quy tắc nhân có 5.6.6.6 = 1080 số.
Cho mẫu số liệu ghép nhóm với bộ ba tứ phân vị lần lượt là \({Q_1} = 11,5\); \({Q_2} = 14,5\); \({Q_3} = 21,3.\) Khi đó khoảng tứ phân vị của mẫu số liệu trên là
-
A.
\(\Delta Q = 3,0\)
-
B.
\(\Delta Q = 6,8\)
-
C.
\(\Delta Q = 9,8\)
-
D.
\(\Delta Q = 32,8\)
Đáp án : C
Khoảng tứ phân vị \(\Delta Q = {Q_3} - {Q_1}\).
Khoảng tứ phân vị của mẫu số liệu là: \(\Delta Q = {Q_3} - {Q_1} = 21,3 - 11,5 = 9,8\).
Nghiệm của phương trình \({3^{{x^2} - 3x + 4}} = 9\) là
-
A.
x = 1; x = 2
-
B.
x = -1; x = 3
-
C.
x = 1; x = -2
-
D.
x = -1; x = 2
Đáp án : A
Đưa hai vế về cùng cơ số.
Ta có \({3^{{x^2} - 3x + 4}} = 9 \Leftrightarrow {3^{{x^2} - 3x + 4}} = {3^2} \Leftrightarrow {x^2} - 3x + 4 = 2 \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\).
Vậy phương trình có hai nghiệm x = 1; x = 2.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, đường thẳng SA vuông góc với mặt phẳng (ABCD) và SA = 3a. Thể tích của khối chóp S.ABCD bằng
-
A.
\(2{a^3}\)
-
B.
\(3{a^3}\)
-
C.
\(6{a^3}\)
-
D.
\({a^3}\)
Đáp án : A
Áp dụng công tính thể tích khối chóp có diện tích đáy B, chiều cao h: \(V = \frac{1}{3}Bh\).
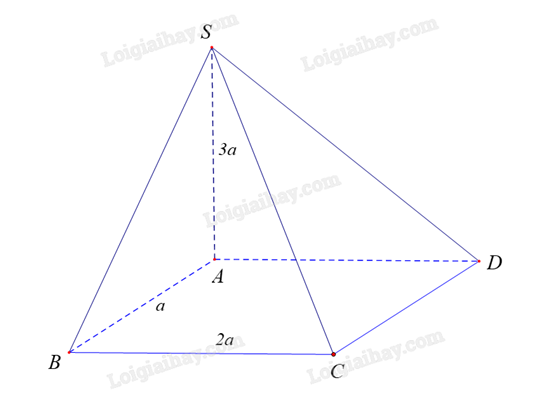
Diện tích đáy \(B = a.2a = 2{a^2}\)và chiều cao bằng \(h = 3a\)
Thể tích khối chóp là: \({V_{S.ABCD}} = \frac{1}{3}.a.2a.3a\)\( = 2{a^3}\).
v
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = \left( {1; - 2;1} \right)\) và \(\overrightarrow b = \left( {2; - 4; - 2} \right)\). Khi đó \(\overrightarrow a .\overrightarrow b \) bằng
-
A.
8
-
B.
-8
-
C.
12
-
D.
-12
Đáp án : A
Áp dụng biểu thức tọa độ tích vô hướng của hai vecto.
Ta có \(\overrightarrow a .\overrightarrow b = 1.2 + \left( { - 2} \right).\left( { - 4} \right) + 1.\left( { - 2} \right) = 8\).
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau:
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
-
A.
[7;9)
-
B.
[9;11)
-
C.
[11;13)
-
D.
[13;15)
Đáp án : B
Lập bảng tần số ghép nhóm theo giá trị đại diện rồi áp dụng công thức tính số trung bình.
Bảng tần số ghép nhóm theo giá trị đại diện là:
Số trung bình: \(\bar x = \frac{{2.6 + 7.8 + 7.10 + 3.12 + 1.14}}{{20}} = 9,4\).
Trong không gian với Oxyz, cho hai điểm A(1;2;3), B(-2;-4;9). Điểm M thuộc đoạn thẳng AB sao cho MA = 2MB. Độ dài đoạn thẳng OM là
-
A.
5
-
B.
3
-
C.
\(\sqrt {17} \)
-
D.
\(3\sqrt 6 \)
Đáp án : D
Áp dụng biểu thức tọa độ các phép cộng, trừ, tích của vecto với một số.
Điểm M thuộc đoạn thẳng AB và MA = 2MB.
Nên \(\overrightarrow {MA} = - 2\overrightarrow {MB} \)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_A} - {x_M} = - 2\left( {{x_B} - {x_M}} \right)\\{y_A} - {y_M} = - 2\left( {{y_B} - {y_M}} \right)\\{z_A} - {z_M} = - 2\left( {{z_B} - {z_M}} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}1 - {x_M} = - 2\left( { - 2 - {x_M}} \right)\\2 - {y_M} = - 2\left( { - 4 - {y_M}} \right)\\3 - {z_M} = - 2\left( {9 - {z_M}} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}3{x_M} = - 3\\3{y_M} = - 6\\3{z_M} = 21\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_M} = - 1\\{y_M} = - 2\\{z_M} = 7\end{array} \right.\)
\( \Rightarrow M\left( { - 1\,; - 2\,;7} \right)\).
Độ dài đoạn thẳng \(OM = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2} + {7^2}} = 3\sqrt 6 \).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-2;7), B(-3;8;-1). Mặt cầu đường kính AB có phương trình là
-
A.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 3} \right)^2} = \sqrt {45} \)
-
B.
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 3} \right)^2} = 45\)
-
C.
\({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 3} \right)^2} = \sqrt {45} \)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 3} \right)^2} = 45\)
Đáp án : D
Phương trình mặt cầu tâm I(a;b;c) bán kính R có phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Gọi I là trung điểm AB ta có \(I\left( { - 1;3;3} \right)\) là tâm mặt cầu.
Bán kính \(R = IA = \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( { - 2 - 3} \right)}^2} + {{\left( {7 - 3} \right)}^2}} = \sqrt {45} .\)
Vậy phương trình mặt cầu cần tìm là \({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 3} \right)^2} = 45\).
Một huấn luyện viên môn bóng rổ thống kê lại số quả bóng được ném vào rổ của một nhóm vận động viên đang tập luyện mỗi người ném 11 lần như sau:
a) Từ biểu đồ, có thể lập được bảng tần số ghép nhóm gồm 5 nhóm biết mỗi nhóm có độ dài là 2.
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên lớn hơn 5.
c) Số trung bình của mẫu số liệu bằng \(\frac{{85}}{{14}}\).
d) Độ lệch chuẩn của mẫu số liệu trên lớn hơn 3.
a) Từ biểu đồ, có thể lập được bảng tần số ghép nhóm gồm 5 nhóm biết mỗi nhóm có độ dài là 2.
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên lớn hơn 5.
c) Số trung bình của mẫu số liệu bằng \(\frac{{85}}{{14}}\).
d) Độ lệch chuẩn của mẫu số liệu trên lớn hơn 3.
Lập bảng tần số ghép nhóm, áp dụng công thức tính khoảng tứ phân vị, số trung bình và độ lệch chuẩn.
a) Đúng. Bảng tần số ghép nhóm thoả mãn yêu cầu:
Vậy có 5 nhóm, mỗi nhóm có độ dài bằng 2.
b) Sai. Gọi \({x_1},{x_2},...,{x_{{x_{28}}}}\) lần lượt là số quả bóng được ném vào rổ của các vận động viên sắp xếp theo thứ tự
không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_7} + {x_8}} \right) \in \left[ {3;5} \right)\) nên tứ phân vị thứ nhất của mẫu số liệu
ghép nhóm là \({Q_1} = 3 + \frac{{\frac{{28}}{4} - 5}}{7}\left( {5 - 3} \right) = \frac{{25}}{7}\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}\left( {{x_{21}} + {x_{22}}} \right) \in \left[ {7;9} \right)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là \({Q_1} = 7 + \frac{{\frac{{3.28}}{4} - 15}}{8}\left( {9 - 7} \right) = \frac{{17}}{2}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{17}}{2} - \frac{{25}}{7} \approx 4,93\).
c) Đúng. Ta có bảng thống kê theo giá trị đại diện:
Cỡ mẫu: n = 28.
Số trung bình của mẫu số liệu: \(\overline x = \frac{1}{{28}}\left( {5.2 + 7.4 + 3.6 + 8.8 + 5.10} \right) = \frac{{85}}{{14}}\).
d) Sai. Phương sai của mẫu số liệu:
\({S^2} = \frac{1}{{28}}\left( {{{5.2}^2} + {{7.4}^2} + {{3.6}^2} + {{8.8}^2} + {{5.10}^2}} \right) - {\left( {\frac{{85}}{{14}}} \right)^2} = \frac{{1539}}{{196}}\).
Độ lệch chuẩn của mẫu số liệu trên là: \(S = \sqrt {\frac{{1539}}{{196}}} \approx 2,802\).
Cho hình chóp S.ABC có mặt bên (SAB) vuông góc với mặt đáy và tam giác đều SAB cạnh 2a. Biết tam giác ABC vuông tại C và cạnh \(AC = a\sqrt 3 \).
a) \(SH \bot (ABC)\) với H là trung điểm AB.
b) \(d\left( {S,(ABC)} \right) = a\sqrt 3 \).
c) \(d\left( {C,(SAB)} \right) = \frac{{a\sqrt 3 }}{3}\).
d) Thể tích của khối chóp S.ABC bằng \(\frac{{{a^3}}}{6}\).
a) \(SH \bot (ABC)\) với H là trung điểm AB.
b) \(d\left( {S,(ABC)} \right) = a\sqrt 3 \).
c) \(d\left( {C,(SAB)} \right) = \frac{{a\sqrt 3 }}{3}\).
d) Thể tích của khối chóp S.ABC bằng \(\frac{{{a^3}}}{6}\).
Áp dụng điều kiện để đường thẳng vuông góc với mặt phẳng, định lý Pythagore, công thức tính thể tích khối chóp.
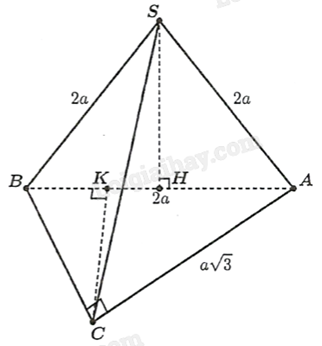
a) Đúng. H là trung điểm AB, mà tam giác SAB đều nên SH vừa là đường trung tuyến, vừa là đường cao, hay \(SH \bot AB\).
Ta có \(\left\{ \begin{array}{l}(SAB) \bot (ABC)\\(SAB) \cap (ABC) = AB\\SH \bot AB\\SH \subset (SAB)\end{array} \right. \Rightarrow SH \bot (ABC)\).
b) Đúng. Tam giác SAB đều cạnh 2a có độ dài đường cao là \(SH = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).
Vì \(\left\{ \begin{array}{l}SH \bot (ABC)\\H \in (ABC)\end{array} \right. \Rightarrow d\left( {S,(ABC)} \right) = SH = a\sqrt 3 \).
c) Sai. Kẻ đường cao CK của tam giác ABC.
Ta có \(\left\{ \begin{array}{l}SH \bot (ABC) \Rightarrow SH \bot CK\\AB \bot CK\end{array} \right. \Rightarrow CK \bot (SAB) \Rightarrow d\left( {C,(SAB)} \right) = CK\).
Áp dụng định lý Pythagore cho tam giác ABC vuông tại C:
\(B{C^2} = \sqrt {A{B^2} - A{C^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {a\sqrt 3 } \right)}^2}} = a\).
Xét tam giác ABC vuông tại C có đường cao CK:
\(AB.CK = CA.CB \Leftrightarrow CK = \frac{{CA.CB}}{{AB}} = \frac{{a\sqrt 3 .a}}{{2a}} = \frac{{a\sqrt 3 }}{2}\).
Vậy \(d\left( {C,(SAB)} \right) = CK = \frac{{a\sqrt 3 }}{2}\).
d) Sai. Diện tích đáy hình chóp là \({S_{ABC}} = \frac{1}{2}AC.BC = \frac{1}{2}a\sqrt 3 .a = \frac{{{a^2}\sqrt 3 }}{2}\).
Thể tích khối chóp là: \({V_{S.ABC}} = \frac{1}{3}SH.{S_{ABC}} = \frac{1}{3}.a\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}}}{2}\).
Cho một cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu bằng -7, số hạng thứ hai bằng 14 và số hạng cuối bằng 14336.
a) Công bội của cấp số nhân bằng 2.
b) 224 là số hạng thứ năm của cấp số nhân đã cho.
c) Cấp số nhân đã cho có 12 số hạng.
d) Tổng \({u_1} + {u_3} + {u_5} + {u_7} + {u_9}\) bằng -2387.
a) Công bội của cấp số nhân bằng 2.
b) 224 là số hạng thứ năm của cấp số nhân đã cho.
c) Cấp số nhân đã cho có 12 số hạng.
d) Tổng \({u_1} + {u_3} + {u_5} + {u_7} + {u_9}\) bằng -2387.
Áp dụng công thức số hạng tổng quát của cấp số nhân \({u_n} = {u_1}{q^{n - 1}}\) và công thức tổng n số hạng đầu của cấp số nhân \({S_n} = \frac{{{q^n} - 1}}{{q - 1}}\).
a) Sai. Công bội của cấp số nhân bằng \(\frac{{{u_2}}}{{{u_1}}} = - 2\).
b) Sai. \({u_5} = - 7.{( - 2)^4} = - 112\).
c) Đúng. \( - 7.{( - 2)^{n - 1}} = 14336 \Leftrightarrow {( - 2)^{n - 1}} = 2048 \Leftrightarrow n - 1 = 11 \Leftrightarrow n = 12\).
d) Đúng. \({u_1},{u_3},{u_5},{u_7},{u_9}\) lập thành một cấp số nhân gồm 5 số hạng với số hạng đầu bằng -7 và công bội bằng 4 nên \({u_1} + {u_3} + {u_5} + {u_7} + {u_9} = - 7.\frac{{{4^5} - 1}}{{4 - 1}} = - 2387\).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình x – y – z – 3 = 0 và hai điểm A(1;-3;-4), B(1;2;1).
a) Mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n = (1; - 1; - 1)\).
b) \(\overrightarrow {AB} = (0;5;5)\).
c) Khoảng cách từ điểm A đến (P) là \(\frac{{5\sqrt 3 }}{3}\).
d) Cho điểm M di động trên (P). Khi đó giá trị nhỏ nhất của biểu thức \(M{A^2} + M{B^2}\) bằng 56.
a) Mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n = (1; - 1; - 1)\).
b) \(\overrightarrow {AB} = (0;5;5)\).
c) Khoảng cách từ điểm A đến (P) là \(\frac{{5\sqrt 3 }}{3}\).
d) Cho điểm M di động trên (P). Khi đó giá trị nhỏ nhất của biểu thức \(M{A^2} + M{B^2}\) bằng 56.
Áp dụng biểu thức tọa độ của các phép toán vecto.
a) Đúng. Ta có \(\overrightarrow {{n_P}} = (1; - 1; - 1)\).
b) Đúng. \(\overrightarrow {AB} = (1 - 1;2 + 3;1 + 4) = (0;5;5)\).
c) Đúng. \(d\left( {A,(P)} \right) = \frac{{\left| {1 - ( - 3) - ( - 4) - 3} \right|}}{{\sqrt {{1^2} + {{( - 1)}^2} + {{( - 1)}^2}} }} = \frac{{5\sqrt 3 }}{3}\).
d) Sai. Gọi I là điểm sao cho \(\overrightarrow {IA} + 4\overrightarrow {IB} = \overrightarrow 0 \), ta có \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{5} = 1\\{y_I} = \frac{{{y_A} + {y_B}}}{5} = 1\\{z_I} = \frac{{{z_A} + {z_B}}}{5} = 0\end{array} \right. \Rightarrow I(1;1;0)\).
Ta có: \(M{A^2} + 4M{B^2} = {\overrightarrow {MA} ^2} + 4{\overrightarrow {MB} ^2} = {\left( {\overrightarrow {IA} - \overrightarrow {IM} } \right)^2} + 4{\left( {\overrightarrow {IB} - \overrightarrow {IM} } \right)^2}\)
\( = 5I{M^2} - 2\overrightarrow {IM} \left( {\overrightarrow {IA} + 4\overrightarrow {IB} } \right) + M{A^2} + 4M{B^2}\).
Suy ra \(M{A^2} + 4M{B^2} = 5I{M^2} + I{A^2} + 4I{B^2}\).
\(M{A^2} + 4M{B^2}\) nhỏ nhất khi IM nhỏ nhất (vì IA, IB cố định) \( \Leftrightarrow \) M là hình chiếu vuông góc của I lên mặt phẳng (P).
Khi đó \(IM = d\left( {I,(P)} \right) = \frac{{\left| {1 - 1 - 0 - 3} \right|}}{{\sqrt {{1^2} + {{( - 1)}^2} + {{( - 1)}^2}} }} = \sqrt 3 \).
\(I{A^2} = {(1 - 1)^2} + {( - 3 - 1)^2} + {( - 4 - 0)^2} = 32\); \(4I{B^2} = 4\left[ {{{(1 - 1)}^2} + {{(2 - 1)}^2} + {{(1 - 0)}^2}} \right] = 8\).
Vậy giá trị nhỏ nhất của \(M{A^2} + 4M{B^2}\) là \(5I{M^2} + I{A^2} + 4I{B^2} = 5.{\left( {\sqrt 3 } \right)^2} + 32 + 8 = 55\).
Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy dài 2,4 m và độ dài các cạnh bên của hình chóp bằng 3 m . Gọi góc nhị diện giữa hai mặt bên đối diện của mái che giếng trời đó là \(\alpha \), tính \(\cos \alpha \) (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Đáp án:
Mô hình hóa mái che dạng chóp tứ giác đều. Áp dụng quy tắc xác định góc nhị diện, định lý Pythagore và hệ quả định lý cosin trong tam giác.
Mái che giếng trời có dạng hình chóp tứ giác đều S.ABCD, SA = 3, AB = 2,4.
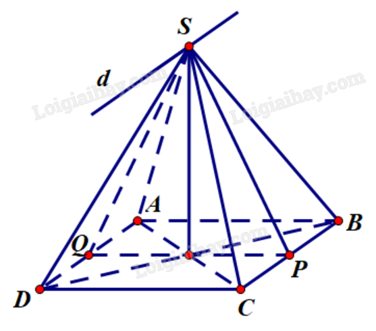
Gọi P, Q là trung điểm của BC, AD. Khi đó \(SP \bot BC\) và \(SQ \bot AD\) (đường trung tuyến đồng thời là đường cao của các tam giác cân đỉnh S).
Vì mỗi mặt phẳng (SBC) và (SAD) chứa đường thằng AD và BC song song với nhau, S là giao điểm của hai mặt phẳng nên tiếp tuyến của chúng là đường thẳng d qua S sao cho d // BC // AD.
Suy ra \(SP \bot d\) và \(SQ \bot d\).
Khi đó \(\widehat {PSQ} = \alpha \) là góc nhị diện giữa hai mặt bên đối diện (SAD), (SBC).
Ta có: SB = 3, PB = 1,2 .
Xét tam giác SPQ: \(\cos \alpha = \frac{{S{P^2} + S{Q^2} - P{Q^2}}}{{2.SP.SQ}} = \frac{{13}}{{21}} \approx 0,62\).
Một bình đựng 30 viên bi kích thước, chất liệu như nhau, trong đó có 20 viên bi xanh và 10 viên bi trắng. Lấy ngẫu nhiên ra một viên bi, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được một viên bi xanh ở lần thứ nhất và một viên bi trắng ở lần thứ hai (làm tròn kết quả đến hàng phần trăm).
Đáp án:
Đáp án:
Áp dụng công thức nhân xác suất \(P(AB) = P(A).P(B|A)\).
A: “Lấy được viên bi xanh ở lần thứ nhất”.
B: “Lấy được viên bi trắng ở lần thứ hai”.
Ban đầu, có 20 viên bi xanh trong tổng số 30 viên bi trắng nên \(P(A) = \frac{{20}}{{30}} = \frac{2}{3}\).
Sau khi lấy được bi xanh ở lần thứ nhất, trong 29 viên bi còn lại có 10 viên bi trắng nên \(P(B|A) = \frac{{10}}{{29}}\).
Xác suất cần tìm là \(P(AB) = P(A).P(B|A) = \frac{2}{3}.\frac{{10}}{{29}} = \frac{{20}}{{87}} \approx 0,23\).
Một người điều khiển một flycam để phục vụ trong một chương trình của đài truyền hình. Đầu tiên flycam ở vị trí A cách vị trí điều khiển 100 m về phía nam và 150 m về phía đông, đồng thời cách mặt đất 30 m. Để thực hiện nhiệm vụ tiếp theo, người đó điều khiển flycam đến vị trí B cách vị trí điều khiển 100 m về phía bắc và 50 m về phía tây, đồng thời cách mặt đất 40 m. Biết flycam bay theo một đường thẳng từ vị trí A đến vị trí B tạo thành một vecto \(\overrightarrow {AB} \). Tính \(\left| {\overrightarrow {AB} } \right|\) (kết quả làm tròn đến hàng đơn vị của mét).
Đáp án:
Đáp án:
Chọn hệ trục tọa độ ở vị trí phù hợp.
Áp dụng công thức tính độ dài vecto \(\left| {\overrightarrow {AB} } \right| = \sqrt {\left( {{x_B} - {x_A}} \right) + \left( {{y_B} - {y_A}} \right)} \).
Chọn hệ trục tọa độ Oxyz , với gốc đặt tại vị trí điều khiển, mặt phẳng (Oxy) trùng với mặt đất, trục Ox hướng về phía nam, trục Oy hướng về phía đông, trục Oz hướng thẳng đứng lên trời, đơn vị đo lấy theo mét (như hình vẽ).
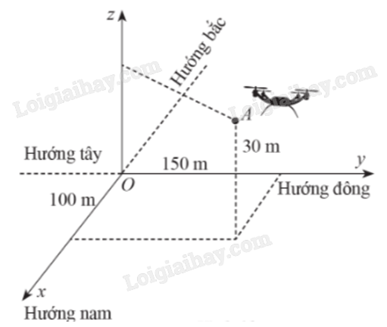
Ta có A(100;150;30), B(-100;-50;40). Suy ra \(\overrightarrow {AB} = ( - 100 - 100; - 50 - 150;40 - 30) = ( - 200; - 200;10)\).
Vậy \(\left| {\overrightarrow {AB} } \right| = \sqrt {{{( - 200)}^2} + {{( - 200)}^2} + {{10}^2}} = 30\sqrt {89} \approx 283\) (m).
Trong 10 giây đầu tiên, một chất điểm chuyển động theo phương trình \(s(t) = {t^3} - 12{t^2} + 5t + 1\), trong đó thời gian t được tính bằng giây, quãng đường s tính bằng mét. Hỏi sau khoảng thời gian bao nhiêu giây thì vận tốc tức thời của chất điểm bắt đầu tăng lên?
Đáp án:
Đáp án:
Lập bảng xét dấu cho hàm v(t) = s’(t).
Vận tốc tức thời của chất điểm tăng lên khi v’(t) đổi dấu từ âm sang dương.
Vận tốc tức thời của chất điểm tại thời điểm \(t\) là \(v(t) = s'(t) = 3{t^2} - 24t + 5\).
Xét hàm số \(v(t) = 3{t^2} - 24t + 5\) với \(t \in \left[ {0;10} \right]\) ta có:
\(v'(t) = 6t - 24 \Rightarrow v'(t) = 0 \Leftrightarrow t = 4\).
Ta có bảng xét dấu:
Từ bảng xét dấu suy ra vận tốc tức thời của chất điểm bắt đầu tăng lên sau khoảng thời gian 4 giây.
Từ một tấm bìa mỏng hình vuông cạnh 6 dm, bạn Hoa cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy là cạnh của hình vuông ban đầu và đỉnh là đỉnh của một hình vuông nhỏ phía trong rồi gập lên, ghép lại tạo thành một khối chóp tứ giác đều (hình vẽ sau).
Thể tích của khối chóp có giá trị lớn nhất bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng phần mười)?
Đáp án:
Đáp án:
Lập hàm số biểu diễn thể tích của khối chóp và tìm giá trị lớn nhất bằng cách ứng dụng đạo hàm.
Gọi cạnh đáy của hình chóp tứ giác đều là x (dm) với \(0 < x < 6\sqrt 2 \) như hình bên.
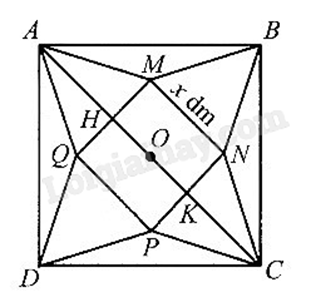
Ta có: \(AH = \frac{{AC - HK}}{2} = 3\sqrt 2 - \frac{x}{2}\).
Đường cao của hình chóp tứ giác đều là: \(h = \sqrt {A{H^2} - O{H^2}} = \sqrt {{{\left( {3\sqrt 2 - \frac{x}{2}} \right)}^2} - {{\left( {\frac{x}{2}} \right)}^2}} = \sqrt {18 - 3\sqrt 2 x} \).
Thể tích khối chóp là: \(V = \frac{1}{3}h{x^2} = \frac{1}{3}{x^2}\sqrt {18 - 3\sqrt 2 x} = \frac{1}{3}\sqrt {{x^4}\left( {18 - 3\sqrt 2 x} \right)} \).
Để tìm giá trị lớn nhất của V, ta đi tìm giá trị lớn nhất của hàm số \(f(x) = {x^4}\left( {18 - 3\sqrt 2 x} \right)\)với \(0 < x < 6\sqrt 2 \).
Ta có: \(f'(x) = {x^3}\left( { - 15\sqrt 2 x + 72} \right)\), \(f'(x) = 0\) khi x = 0 hoặc \(x = \frac{{12\sqrt 2 }}{5}\).
Bảng biến thiên của f(x) như sau:
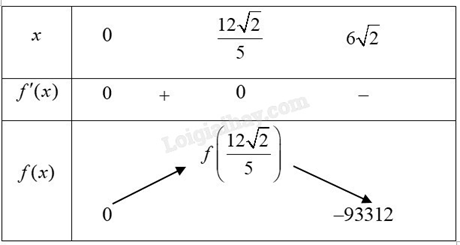
Từ bảng biến thiên ta có \(\mathop {\max }\limits_{\left( {0;6\sqrt 2 } \right)} f(x) = f\left( {\frac{{12\sqrt 2 }}{5}} \right) \approx 477,75\) tại \(x = \frac{{12\sqrt 2 }}{5}\).
Vậy thể tích của khối chóp có giá trị lớn nhất bằng \(V = \frac{1}{3}.\sqrt {{{\left( {\frac{{12\sqrt 2 }}{5}} \right)}^4}\left( {18 - 3\sqrt 2 .\frac{{12\sqrt 2 }}{5}} \right)} \approx 7,3\) \(\left( {d{m^3}} \right)\).
Cho đường thẳng \(y = \frac{3}{4}x\) và parabol \(y = \frac{1}{2}{x^2} + a\), (\(a\) là tham số thực dương). Gọi \({S_1}\), \({S_2}\) lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi \({S_1} = {S_2}\) thì giá trị biểu thức 128a + 3 bằng bao nhiêu?
Đáp án:
Đáp án:
Áp dụng công thức tính diện tích hình phẳng \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \).
Ta có phương trình hoành độ giao điểm \(\frac{1}{2}{x^2} - \frac{3}{4}x + a = 0 \Leftrightarrow 2{x^2} - 3x + 4a = 0\).
Theo đề bài phương trình có hai nghiệm \(0 < {x_1} < {x_2}\) thỏa mãn \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{3}{2}\quad \left( * \right)\\{x_1}{x_2} = 2a\quad \,\,\left( {**} \right)\end{array} \right.\).
\({S_1} - {S_2} = 0 \Leftrightarrow \int\limits_0^{{x_1}} {\left| {\frac{1}{2}{x^2} - \frac{3}{4}x + a} \right|{\rm{d}}x} + \int\limits_{{x_1}}^{{x_2}} {\left| {\frac{1}{2}{x^2} - \frac{3}{4}x + a} \right|{\rm{d}}x} = 0 \Leftrightarrow \int\limits_0^{{x_2}} {\left| {\frac{1}{2}{x^2} - \frac{3}{4}x + a} \right|{\rm{d}}x} = 0\)
\( \Leftrightarrow \left. {\left| {\frac{1}{6}{x^3} - \frac{3}{8}{x^2} + ax} \right|} \right|_0^{{x_2}} = 0 \Leftrightarrow \left| {\frac{1}{6}x_2^3 - \frac{3}{8}x_2^2 + a{x_2}} \right| = 0 \Rightarrow a = - \frac{{x_2^2}}{6} + \frac{{3{x_2}}}{8}\) (***).
Từ \(\left( * \right) \Rightarrow {x_1} = \frac{3}{2} - {x_2}\), thay vào \(\left( {**} \right) \Rightarrow \left( {\frac{3}{2} - {x_2}} \right){x_2} = - \frac{{x_2^2}}{3} + \frac{{3{x_2}}}{4} \Leftrightarrow \frac{{2x_2^2}}{3} - \frac{{3{x_2}}}{4} = 0 \Rightarrow {x_2} = \frac{9}{8}\).
Thay vào (***) ta được \(a = \frac{{27}}{{128}}\).
Vậy \(128a + 3 = 128.\frac{{27}}{{128}} + 3 = 30\).
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Các bài khác cùng chuyên mục
