Đề tham khảo thi THPT môn Toán - Đề số 8 (hay, chi tiết)
I. Phần trắc nghiệm
Đề bài
Trong không gian Oxyz, cho đường thẳng d: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 3 - t\\z = 2 - 3t\end{array} \right.\), \(t \in \mathbb{R}\), một vecto chỉ phương của đường thẳng d là
-
A.
\(\overrightarrow c = ( - 1;3; - 2)\)
-
B.
\(\overrightarrow d = (2;1; - 3)\)
-
C.
\(\overrightarrow a = ( - 2;1;3)\)
-
D.
\(\overrightarrow b = (1; - 3;2)\)
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [-1;3], biết f(3) = 5; f(-1) = -2; giá trị của \(\int\limits_{ - 1}^3 {f'(x)dx} \) là
-
A.
7
-
B.
3
-
C.
4
-
D.
-7
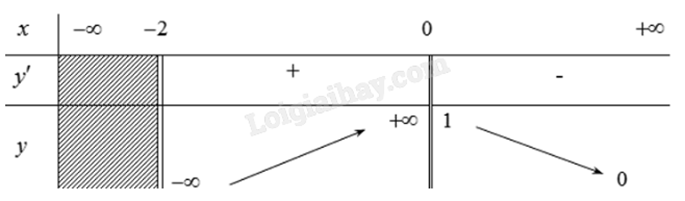
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận đứng?
-
A.
3
-
B.
2
-
C.
4
-
D.
1
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\); \({u_2} = 6\). Giá trị \({u_5}\) là
-
A.
27
-
B.
54
-
C.
81
-
D.
162
Trong cuộc thi có 10 thí sinh tham gia, số cách trao một giải nhất, một giải nhì và một giải ba là
-
A.
\({10^3}\)
-
B.
\(3.10\)
-
C.
\(A_{10}^3\)
-
D.
\(C_{10}^3\)
Bạn Hằng rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Hằng được thống kê lại ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
-
A.
25,75
-
B.
27,5
-
C.
31,88
-
D.
8,125
\({\Delta _Q} = {Q_3} - {Q_1}\).
Phương trình \({\log _3}(2x - 3) = 3\) có nghiệm là
-
A.
12
-
B.
15
-
C.
13
-
D.
6
Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh là 3a, \(SA \bot (ABCD)\), \(SA = a\sqrt 2 \). Thể tích khối chóp S.ABCD là
-
A.
\(3{a^3}\sqrt 2 \)
-
B.
\(4{a^3}\sqrt 2 \)
-
C.
\(9{a^3}\sqrt 2 \)
-
D.
\(12{a^3}\sqrt 2 \)
Cho hình chóp S.ABCD có ABCD là hình chữ nhật với AB = 3, AD = 4, \(SA \bot (ABCD)\), SA = 5. Giá trị của \(\overrightarrow {SA} .\overrightarrow {BC} \) là
-
A.
15
-
B.
12
-
C.
20
-
D.
0
Bác Hùng thống kê lại đường kính thân gỗ của một số cây Keo tai tượng 5 năm tuổi được trồng ở
một lâm trường ở bảng sau:

Hãy tìm số trung bình cộng của mẫu số liệu ghép nhóm trên.
-
A.
36,9 cm
-
B.
33,9 cm
-
C.
35,9 cm
-
D.
34,9 cm
Trong không gian (Oxyz), cho \(\Delta ABC\) có \(\overrightarrow {AB} = (4; - 1; - 5)\), \(\overrightarrow {BC} = (2; - 4; - 2)\), gọi M là trung điểm BC. Độ dài đoạn AM là
-
A.
\(\sqrt {70} \)
-
B.
\(2\sqrt {70} \)
-
C.
\(\sqrt 6 \)
-
D.
\(\frac{{\sqrt {110} }}{2}\)
Trong không gian (Oxyz), cho mặt phẳng (P): 2x – y – z + 4 = 0 và điểm I(2;-3;-1); mặt cầu (S) tâm I và tiếp xúc mặt phẳng (P) có phương trình là
-
A.
\({(x - 2)^2} + {(y + 3)^2} + {(z + 1)^2} = 12\)
-
B.
\({(x - 2)^2} + {(y + 3)^2} + {(z + 1)^2} = 24\)
-
C.
\({(x + 2)^2} + {(y - 3)^2} + {(z - 1)^2} = 12\)
-
D.
\({(x + 2)^2} + {(y - 3)^2} + {(z - 1)^2} = 24\)
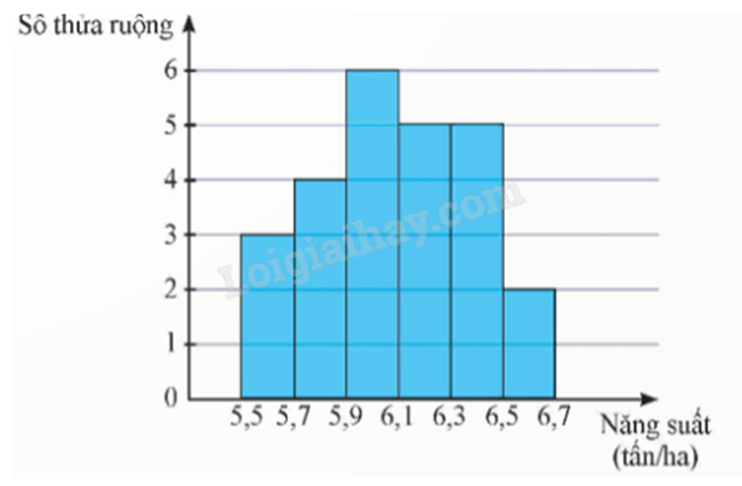
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:
a) Có 25 thửa ruộng đã được khảo sát.
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 6,33.
d) Phương sai của mẫu số liệu ghép nhóm trên là 0,086656.
Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\), đáy ABCD là hình chữ nhật với \(AC = a\sqrt 5 \) và \(AD = a\sqrt 2 \). Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng \(\frac{{a\sqrt 3 }}{2}\).
a) Đường cao của hình chóp S.ABCD là SA.
b) Khoảng cách từ điểm A đến mặt phẳng (SBC) là \(AH = \frac{{a\sqrt 3 }}{2}\), với AH là đường cao của tam giác SAB.
c) Thể tích của khối chóp \(S.ABC\) bằng \(\frac{{{a^3}\sqrt 6 }}{3}\).
d) Gọi M, N lần lượt là trung điểm của AB và CD. Khoảng cách giữa hai đường thẳng MN và SB bằng \(\frac{{a\sqrt 3 }}{2}\).
Cho dãy số \(\left( {{u_n}} \right)\): \(\left\{ \begin{array}{l}{u_1} = 2\\{u_n} = 2{u_{n - 1}} + 2 - n\end{array} \right.,\forall n \ge 2\).
a) \({u_2} = 4\).
b) \({u_n} - n = 2{u_{n - 1}} - \left( {n - 1} \right)\).
c) Đặt \({v_n} = {u_n} - n\) thì dãy số \(\left( {{v_n}} \right)\) là cấp số nhân.
d) \({S_{100}} = 2524 + {2^{99}}\).
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’, biết rằng A(1;2;0), A’(1;0;1), B(1;5;1), D’(0;-2;0).
a) Tọa độ vecto \(\overrightarrow {AA'} \) là \(\overrightarrow {AA'} = \left( {0; - 2;1} \right)\).
b) Tọa độ các điểm B’, C là B’(2;1;-1), C(0;3;0).
c) \(AB = \sqrt {10} \); \(C'A = \sqrt 3 \).
d) Đặt \(P = M{A^2} + M{B^2} + M{C^2} + M{D^2}\). P đạt giá trị nhỏ nhất khi M(1;-2;0).
Hai mái nhà trong hình bên là hai hình chữ nhật. Giả sử AB = 3,8 m; OA = 2,2 m; OB = 3 m. Gọi \(\alpha \) là góc phẳng nhị diện tạo bởi hai mái nhà và \(\cos \alpha = \frac{m}{n}\) với \(\frac{m}{n}\) là phân số tối giản và \(m \in \mathbb{Z},n \in \mathbb{N}\). Tính \(3m + {n^2}\)?

Đáp án:
Trong phép thử T, cho A và B là hai biến cố độc lập nhau. Biết P(A) + P(B) = 1,1 và P(AB) = 0,3. Tính xác suất của biến cố \(\overline A .\overline B \).
Đáp án:
Một tháp trung tâm kiểm soát không lưu ở sân bay cao 80 m sử dụng ra đa có phạm vi theo dõi 500 km được đặt trên đỉnh tháp. Chọn hệ trục toạ độ Oxyz có gốc O trùng với vị trí chân tháp, mặt phẳng (Oxy) trùng với mặt đất sao cho trục Ox hướng về phía tây, trục Oy hướng về phía nam, trục Oz hướng thẳng đứng lên phía trên (đơn vị trên mỗi trục tính theo kilômét).

Một máy bay tại vị trí A cách mặt đất 10 km, cách 300 km về phía đông và 200 km về phía bắc so với tháp trung tâm kiểm soát không lưu. Khoảng cách từ máy bay đến ra đa bằng bao nhiêu ki-lô-mét (làm tròn kết quả đến hàng đơn vị)?
Đáp án:
Một ngọn hải đăng được đặt tại vị trí A cách bờ biển một khoảng AB = 5 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng 7 km. Người canh hải đăng có thể chèo đò từ A đến địa điểm M trên bờ biển với vận tốc 4 km/h, rồi đi bộ đến C với vận tốc 6 km/h.
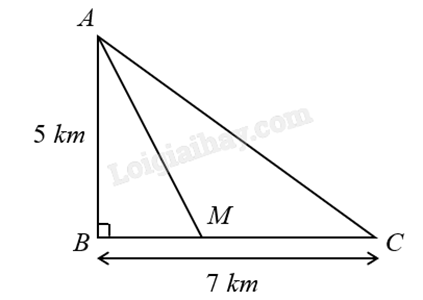
Vị trí của M cách B một khoảng bằng bao nhiêu ki-lô-mét thì người canh hải đăng đến kho nhanh nhất (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Một tấm bạt hình vuông cạnh 20 m như hình vẽ dưới đây. Người ta dự tính cắt phần tô đậm của tấm bạt rồi gập và may lại (các đường may không đáng kể), nhằm mục đích phủ lên tháp đèn trang trí (tháp dạng hình chóp tứ giác đều) để tránh hư hại tháp khi trời mưa.
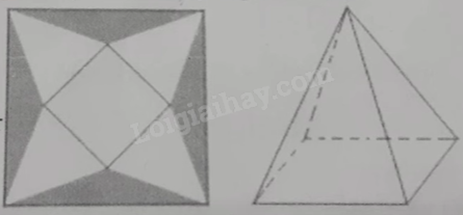
Biết khối chóp hình thành sau khi gập và may lại cần thể tích lớn nhất thì mới phủ kín tháp đèn. Hỏi phần diện tích tấm bạt bị cắt là bao nhiêu để đảm bảo yêu cầu trên?
Đáp án:
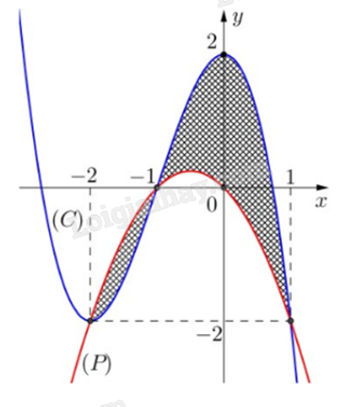
Biết hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Tính diện tích phần kẻ hình ca-rô của hình vẽ (kết quả làm tròn đến hàng phần trăm).
Đáp án:
Lời giải và đáp án
Trong không gian Oxyz, cho đường thẳng d: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 3 - t\\z = 2 - 3t\end{array} \right.\), \(t \in \mathbb{R}\), một vecto chỉ phương của đường thẳng d là
-
A.
\(\overrightarrow c = ( - 1;3; - 2)\)
-
B.
\(\overrightarrow d = (2;1; - 3)\)
-
C.
\(\overrightarrow a = ( - 2;1;3)\)
-
D.
\(\overrightarrow b = (1; - 3;2)\)
Đáp án : C
Đường thẳng d: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) có một vecto chỉ phương là \(\overrightarrow u = (a;b;c)\).
Một vecto chỉ phương của d là \(\overrightarrow u = (2; - 1; - 3)\). Do \(\overrightarrow a = ( - 2;1;3)\) cùng phương với \(\overrightarrow u = (2; - 1; - 3)\) nên \(\overrightarrow a = ( - 2;1;3)\) cũng là một vecto chỉ phương của d.
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [-1;3], biết f(3) = 5; f(-1) = -2; giá trị của \(\int\limits_{ - 1}^3 {f'(x)dx} \) là
-
A.
7
-
B.
3
-
C.
4
-
D.
-7
Đáp án : A
\(\int\limits_a^b {f'(x)dx} = f(x)\left| {\begin{array}{*{20}{c}}{^b}\\{_a}\end{array}} \right. = f(b) - f(a)\).
\(\int\limits_{ - 1}^3 {f'(x)dx} = f(x)\left| {\begin{array}{*{20}{c}}{^3}\\{_{ - 1}}\end{array} = f(3) - f( - 1) = 5 - ( - 2) = 7} \right.\).
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận đứng?

-
A.
3
-
B.
2
-
C.
4
-
D.
1
Đáp án : B
\({x_0}\) là tiệm cận đứng của đồ thị y = f(x) khi thỏa mãn một trong các điều kiện sau: \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \); \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \).
Quan sát bảng biến thiên, thấy \(\mathop {\lim }\limits_{x \to - {2^ - }} f(x) = - \infty \) và \(\mathop {\lim }\limits_{x \to {0^ - }} f(x) = + \infty \).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\); \({u_2} = 6\). Giá trị \({u_5}\) là
-
A.
27
-
B.
54
-
C.
81
-
D.
162
Đáp án : D
Áp dụng công thức số hạng tổng quát của cấp số nhân: \({u_n} = {u_1}{q^{n - 1}}\).
\(q = \frac{{{u_2}}}{{{u_1}}} = \frac{6}{2} = 3\); \({u_5} = {u_1}{q^4} = {2.3^4} = 162\).
Trong cuộc thi có 10 thí sinh tham gia, số cách trao một giải nhất, một giải nhì và một giải ba là
-
A.
\({10^3}\)
-
B.
\(3.10\)
-
C.
\(A_{10}^3\)
-
D.
\(C_{10}^3\)
Đáp án : C
Áp dụng chỉnh hợp.
Số cách trao một giải nhất, một giải nhì và một giải ba cho 3 trong số 10 thí sinh là \(A_{10}^3\).
Bạn Hằng rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn Hằng được thống kê lại ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
-
A.
25,75
-
B.
27,5
-
C.
31,88
-
D.
8,125
\({\Delta _Q} = {Q_3} - {Q_1}\).
Đáp án : D
\({\Delta _Q} = {Q_3} - {Q_1}\).
Cỡ mẫu: n = 6 + 6 + 4 + 1 + 1 = 18.
\({Q_2} = \frac{1}{2}\left( {{x_9} + {x_{10}}} \right)\);
\({Q_1} = {x_5} \in [20;25) \Rightarrow {Q_1} = 20 + \frac{{\frac{{18}}{4} - 0}}{6}(25 - 20) = \frac{{95}}{4}\);
\({Q_3} = {x_{14}} \in [30;35) \Rightarrow {Q_3} = 30 + \frac{{\frac{{3.18}}{4} - 12}}{4}(35 - 30) = \frac{{225}}{8}\);
\({\Delta _Q} = {Q_3} - {Q_1} = \frac{{225}}{8} - \frac{{95}}{4} = 8,125\).
Phương trình \({\log _3}(2x - 3) = 3\) có nghiệm là
-
A.
12
-
B.
15
-
C.
13
-
D.
6
Đáp án : B
\({\log _a}x = b \Leftrightarrow x = {a^b}\), điều kiện b > 0.
ĐKXĐ: \(2x - 3 > 0 \Leftrightarrow x > \frac{3}{2}\).
\({\log _3}(2x - 3) = 3 \Leftrightarrow 2x - 3 = {3^3} \Leftrightarrow x = 15\).
Cho khối chóp S.ABCD có ABCD là hình vuông có cạnh là 3a, \(SA \bot (ABCD)\), \(SA = a\sqrt 2 \). Thể tích khối chóp S.ABCD là
-
A.
\(3{a^3}\sqrt 2 \)
-
B.
\(4{a^3}\sqrt 2 \)
-
C.
\(9{a^3}\sqrt 2 \)
-
D.
\(12{a^3}\sqrt 2 \)
Đáp án : A
Áp dụng công thức \(V = \frac{1}{3}Bh\) tính thể tích khối chóp có diện tích đáy là B, chiều cao là h.
\(SA \bot (ABCD)\) nên chiều cao khối chóp là SA.
\({V_{S.ABCD}} = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}.a\sqrt 2 .\left( {3{a^2}} \right) = 3{a^3}\sqrt 2 \).
Cho hình chóp S.ABCD có ABCD là hình chữ nhật với AB = 3, AD = 4, \(SA \bot (ABCD)\), SA = 5. Giá trị của \(\overrightarrow {SA} .\overrightarrow {BC} \) là
-
A.
15
-
B.
12
-
C.
20
-
D.
0
Đáp án : D
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Vì \(SA \bot (ABCD)\) nên \(SA \bot BC\), khi đó \(\overrightarrow {SA} .\overrightarrow {BC} = 0\).
Bác Hùng thống kê lại đường kính thân gỗ của một số cây Keo tai tượng 5 năm tuổi được trồng ở
một lâm trường ở bảng sau:

Hãy tìm số trung bình cộng của mẫu số liệu ghép nhóm trên.
-
A.
36,9 cm
-
B.
33,9 cm
-
C.
35,9 cm
-
D.
34,9 cm
Đáp án : C
Áp dụng công thức \(\overline x = \frac{{{c_1}{n_1} + {c_2}{n_2} + ... + {c_k}{n_k}}}{{{n_1} + {n_2} + ... + {n_k}}}\).

\(\overline x = \frac{{27,5.5 + 32,5.20 + 37,5.18 + 42,5.7 + 47,5.3}}{{5 + 20 + 18 + 7 + 3}} \approx 35,9\).
Trong không gian (Oxyz), cho \(\Delta ABC\) có \(\overrightarrow {AB} = (4; - 1; - 5)\), \(\overrightarrow {BC} = (2; - 4; - 2)\), gọi M là trung điểm BC. Độ dài đoạn AM là
-
A.
\(\sqrt {70} \)
-
B.
\(2\sqrt {70} \)
-
C.
\(\sqrt 6 \)
-
D.
\(\frac{{\sqrt {110} }}{2}\)
Đáp án : A
Áp dụng quy tắc ba điểm tính \(\overrightarrow {AC} \), quy tắc trung điểm tính \(\overrightarrow {AM} \). Từ đó, tìm độ dài AM.
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} = (4 + 2; - 1 - 4; - 5 - 2) = (6; - 5; - 7)\); \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{2}\left( {4 + 6; - 1 - 5; - 5 - 7} \right) = \left( {5; - 3; - 6} \right)\).
Suy ra \(AM = \sqrt {{5^2} + {{( - 3)}^2} + {{( - 6)}^2}} = \sqrt {70} \).
Trong không gian (Oxyz), cho mặt phẳng (P): 2x – y – z + 4 = 0 và điểm I(2;-3;-1); mặt cầu (S) tâm I và tiếp xúc mặt phẳng (P) có phương trình là
-
A.
\({(x - 2)^2} + {(y + 3)^2} + {(z + 1)^2} = 12\)
-
B.
\({(x - 2)^2} + {(y + 3)^2} + {(z + 1)^2} = 24\)
-
C.
\({(x + 2)^2} + {(y - 3)^2} + {(z - 1)^2} = 12\)
-
D.
\({(x + 2)^2} + {(y - 3)^2} + {(z - 1)^2} = 24\)
Đáp án : B
Mặt cầu (S) tiếp xúc mặt phẳng (P) nên khoảng cách từ tâm I đến (P) là bán kính mặt cầu.
\(R = d\left( {I,(P)} \right) = \frac{{\left| {2.2 - ( - 3) - ( - 1) + 4} \right|}}{{\sqrt {{2^2} + {{( - 1)}^2} + {{( - 1)}^2}} }} = 2\sqrt 6 \).
Phương trình mặt cầu (S) là \({(x - 2)^2} + {(y + 3)^2} + {(z + 1)^2} = 24\).
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:

a) Có 25 thửa ruộng đã được khảo sát.
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 6,33.
d) Phương sai của mẫu số liệu ghép nhóm trên là 0,086656.
a) Có 25 thửa ruộng đã được khảo sát.
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha).
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là 6,33.
d) Phương sai của mẫu số liệu ghép nhóm trên là 0,086656.
Lập bảng tần số ghép nhóm từ biểu đồ. Áp dụng công thức tính khoảng biến thiên, khoảng tứ phân vị, phương sai của mẫu số liệu ghép nhóm.
a) Đúng. Số thửa ruộng được khảo sát là: n = 3 + 4 + 6 + 5 + 5 + 2 = 25.
b) Đúng. Từ biểu đồ, ta có bảng tần số ghép nhóm của mẫu số liệu như sau:
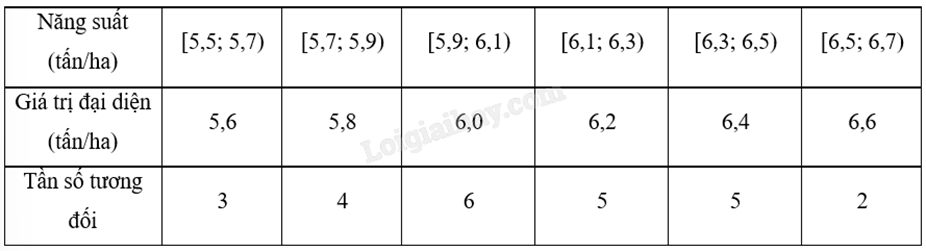
Khoảng biến thiên của mẫu số liệu đã cho là: R = 6,7 – 5,5 = 1,2 (tấn/ha).
c) Sai. Ta có:
Cỡ mẫu n = 25.
Gọi \({x_1};...;{x_{25}}\) là mẫu số liệu gốc về năng suất của một số thửa ruộng được khảo sát được xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{{{x_6} + {x_7}}}{2} \in \) [5,7; 5,9). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 5,7 + \frac{{\frac{{25}}{4} - 3}}{4}\left( {5,9 - 5,7} \right) = 5,8625\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{{{x_{19}} + {x_{20}}}}{2} \in \) [6,3; 6,5). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 6,3 + \frac{{\frac{{3.25}}{4} - \left( {3 + 4 + 6 + 5} \right)}}{5}\left( {6,5 - 6,3} \right) = 6,33\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 6,33 - 5,8625 = 0,4675\).
d) Đúng. Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{3.5,6 + 4.5,8 + 6.6,2 + 5.6,4 + 2.6,6}}{{25}} = 6,088\).
Phương sai của mẫu số liệu ghép nhóm là:
\({S^2} = \frac{1}{{25}}\left[ {3.{{\left( {5,6} \right)}^2} + 4.{{\left( {5,8} \right)}^2} + 6.{{\left( {6,0} \right)}^2} + 5.{{\left( {6,2} \right)}^2} + 5.{{\left( {6,4} \right)}^2} + 2.{{\left( {6,6} \right)}^2}} \right] - {\left( {6,088} \right)^2} = 0,086656\).
Cho hình chóp S.ABCD có \(SA \bot \left( {ABCD} \right)\), đáy ABCD là hình chữ nhật với \(AC = a\sqrt 5 \) và \(AD = a\sqrt 2 \). Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng \(\frac{{a\sqrt 3 }}{2}\).
a) Đường cao của hình chóp S.ABCD là SA.
b) Khoảng cách từ điểm A đến mặt phẳng (SBC) là \(AH = \frac{{a\sqrt 3 }}{2}\), với AH là đường cao của tam giác SAB.
c) Thể tích của khối chóp \(S.ABC\) bằng \(\frac{{{a^3}\sqrt 6 }}{3}\).
d) Gọi M, N lần lượt là trung điểm của AB và CD. Khoảng cách giữa hai đường thẳng MN và SB bằng \(\frac{{a\sqrt 3 }}{2}\).
a) Đường cao của hình chóp S.ABCD là SA.
b) Khoảng cách từ điểm A đến mặt phẳng (SBC) là \(AH = \frac{{a\sqrt 3 }}{2}\), với AH là đường cao của tam giác SAB.
c) Thể tích của khối chóp \(S.ABC\) bằng \(\frac{{{a^3}\sqrt 6 }}{3}\).
d) Gọi M, N lần lượt là trung điểm của AB và CD. Khoảng cách giữa hai đường thẳng MN và SB bằng \(\frac{{a\sqrt 3 }}{2}\).
Áp dụng điều kiện để đường thẳng vuông góc với mặt phẳng, hệ thức lượng trong tam giác vuông.
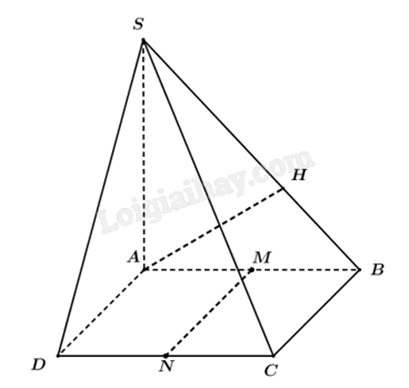
a) Đúng. Ta có \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot \left( {ABC} \right)\). Do đó SA là đường cao của hình chóp S.ABC.
b) Đúng. Trong mặt phẳng \(\left( {SAB} \right)\), kẻ \(AH \bot SB\), \(H \in SB\) (1)
Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right),AH \subset \left( {SAB} \right) \Rightarrow BC \bot AH\) (2)
Từ (1), (2) \( \Rightarrow \)\(AH \bot \left( {SBC} \right)\).
Do đó \(d\left( {A;\left( {SBC} \right)} \right) = AH = \frac{{a\sqrt 3 }}{2}\).
c) Sai. Ta có \(AB = \sqrt {A{C^2} - B{C^2}} = a\sqrt 3 \).
Xét trong tam giác vuông \(SAB\) có \(AH\) là đường cao, ta có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} \Leftrightarrow \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} \Leftrightarrow SA = a\).
Do đó: \({V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SA = \frac{1}{3}.\frac{1}{2}AB.BC.SA = \frac{1}{3}.\frac{1}{2}.a\sqrt 3 .a\sqrt 2 .a = \frac{{{a^3}\sqrt 6 }}{6}\).
d) Sai. Ta có:
\(\left. \begin{array}{l}MN{\rm{//}}BC\\MN \not\subset \left( {SBC} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow MN{\rm{//}}\left( {SBC} \right)\).
Do đó \(d\left( {MN;SB} \right) = d\left( {MN;\left( {SBC} \right)} \right) = d\left( {M;\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A;\left( {SBC} \right)} \right) = \frac{1}{2}AH = \frac{{a\sqrt 3 }}{4}\).
Cho dãy số \(\left( {{u_n}} \right)\): \(\left\{ \begin{array}{l}{u_1} = 2\\{u_n} = 2{u_{n - 1}} + 2 - n\end{array} \right.,\forall n \ge 2\).
a) \({u_2} = 4\).
b) \({u_n} - n = 2{u_{n - 1}} - \left( {n - 1} \right)\).
c) Đặt \({v_n} = {u_n} - n\) thì dãy số \(\left( {{v_n}} \right)\) là cấp số nhân.
d) \({S_{100}} = 2524 + {2^{99}}\).
a) \({u_2} = 4\).
b) \({u_n} - n = 2{u_{n - 1}} - \left( {n - 1} \right)\).
c) Đặt \({v_n} = {u_n} - n\) thì dãy số \(\left( {{v_n}} \right)\) là cấp số nhân.
d) \({S_{100}} = 2524 + {2^{99}}\).
Thay số vào công thức đã cho.
\(\left( {{v_n}} \right)\) là cấp số nhân khi \({v_n} = q.{v_{n - 1}}\) (q là hằng số).
Áp dụng công thức tổng n số hạng đầu của cấp số nhân \(S = {u_1}\frac{{1 - {q^n}}}{{1 - q}}\).
a) Đúng. Ta có: \({u_2} = 2.{u_1} + 2 - 2 = 2.2 = 4\).
b) Sai. Ta có: \({u_n} - n = 2\left( {{u_{n - 1}} - \left( {n - 1} \right)} \right)\).
c) Đúng. Đặt \({v_n} = {u_n} - n\) thì \({v_{n - 1}} = {u_{n - 1}} - \left( {n - 1} \right)\). Mà \({u_n} - n = 2\left( {{u_{n - 1}} - \left( {n - 1} \right)} \right)\) nên \({v_n} = 2{v_{n - 1}}\) dãy số \(\left( {{v_n}} \right)\) là cấp số nhân.
d) Đúng. Từ \({v_n} = 2{v_{n - 1}}\) dãy số \(\left( {{v_n}} \right)\) là cấp số nhân có \({v_1} = 1,\) công bội \(q = 2\) nên số hạng tổng quát \({v_n} = {v_1}.{q^{n - 1}} = {2^{n - 1}}\) mà \({v_n} = {u_n} - n\) nên \({2^{n - 1}} = {u_n} - n \Leftrightarrow {u_n} = {2^{n - 1}} + n\).
\({S_{100}} = \left( {{2^0} + {2^1} + ... + {2^{99}}} \right) + \left( {1 + 2 + ... + 100} \right) = \frac{{1\left( {1 - {2^{99}}} \right)}}{{1 - 2}} + \frac{{\left( {1 + 100} \right)50}}{2} = 2524 + {2^{99}}\).
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A’B’C’D’, biết rằng A(1;2;0), A’(1;0;1), B(1;5;1), D’(0;-2;0).
a) Tọa độ vecto \(\overrightarrow {AA'} \) là \(\overrightarrow {AA'} = \left( {0; - 2;1} \right)\).
b) Tọa độ các điểm B’, C là B’(2;1;-1), C(0;3;0).
c) \(AB = \sqrt {10} \); \(C'A = \sqrt 3 \).
d) Đặt \(P = M{A^2} + M{B^2} + M{C^2} + M{D^2}\). P đạt giá trị nhỏ nhất khi M(1;-2;0).
a) Tọa độ vecto \(\overrightarrow {AA'} \) là \(\overrightarrow {AA'} = \left( {0; - 2;1} \right)\).
b) Tọa độ các điểm B’, C là B’(2;1;-1), C(0;3;0).
c) \(AB = \sqrt {10} \); \(C'A = \sqrt 3 \).
d) Đặt \(P = M{A^2} + M{B^2} + M{C^2} + M{D^2}\). P đạt giá trị nhỏ nhất khi M(1;-2;0).
Áp dụng biểu thức tọa độ các phép toán trong không gian.
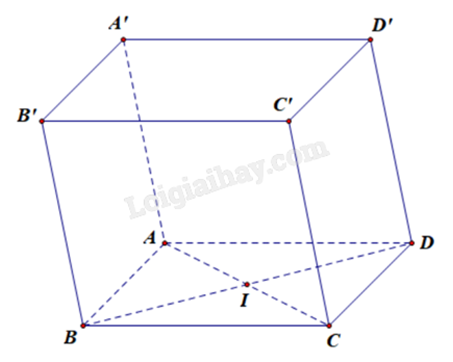
a) Đúng. Tọa độ vecto \(\overrightarrow {AA'} \) là \(\overrightarrow {AA'} = \left( {1 - 1;0 - 2;1 - 0} \right) = \left( {0; - 2;1} \right)\).
b) Sai. \(\overrightarrow {AA'} = \left( {0; - 2;1} \right) = \overrightarrow {BB'} \); \(B\left( {1;5;1} \right) \Rightarrow B'\left( {1;3;2} \right)\).
\(\overrightarrow {A'D'} = \left( { - 1; - 2; - 1} \right) = \overrightarrow {BC} \); \(B\left( {1;5;1} \right) \Rightarrow C\left( {0;3;0} \right)\).
c) Đúng. Ta có \[\overrightarrow {AB} \left( {0;3;1} \right) \Rightarrow AB = \sqrt {{0^2} + {3^2} + {1^2}} = \sqrt {10} \].
\(\overrightarrow {AA'} = \left( {0; - 2;1} \right) = \overrightarrow {CC'} \); \(C\left( {0;3;0} \right) \Rightarrow C'\left( {0;1;1} \right) \Rightarrow AC' = \sqrt {{{\left( {0 - 1} \right)}^2} + {{\left( {1 - 2} \right)}^2} + {{\left( {1 - 0} \right)}^2}} = \sqrt 3 \).
d) Sai. Ta có:
\(P = \,M{A^2} + M{B^2} + M{C^2} + M{D^2} = {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {ID} } \right)^2}\)
\( = 4M{I^2} + 2\overrightarrow {MI} .\left( {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right) + I{A^2} + I{B^2} + I{C^2} + I{D^2} = 4M{I^2} + I{A^2} + I{B^2} + I{C^2} + I{D^2}\).
Do đó, P đạt giá trị nhỏ nhất khi và chỉ khi \(MI\)nhỏ nhất hay \(M \equiv I\).
\(\overrightarrow {A'D'} = \left( { - 1; - 2; - 1} \right) = \overrightarrow {AD} \); \(A\left( {1;2;0} \right) \Rightarrow D\left( {0;0; - 1} \right)\).
\(I\) là trung điểm \(BD\)\( \Rightarrow I\left( {\frac{{1 + 0}}{2};\frac{{5 + 0}}{2};\frac{{1 - 1}}{2}} \right) \Rightarrow I\left( {\frac{1}{2};\frac{5}{2};0} \right)\) hay \(M\left( {\frac{1}{2};\frac{5}{2};0} \right)\).
Hai mái nhà trong hình bên là hai hình chữ nhật. Giả sử AB = 3,8 m; OA = 2,2 m; OB = 3 m. Gọi \(\alpha \) là góc phẳng nhị diện tạo bởi hai mái nhà và \(\cos \alpha = \frac{m}{n}\) với \(\frac{m}{n}\) là phân số tối giản và \(m \in \mathbb{Z},n \in \mathbb{N}\). Tính \(3m + {n^2}\)?

Đáp án:
Đáp án:
Áp dụng quy tắc xác định góc nhị diện và định lý cosin cho tam giác để tính.
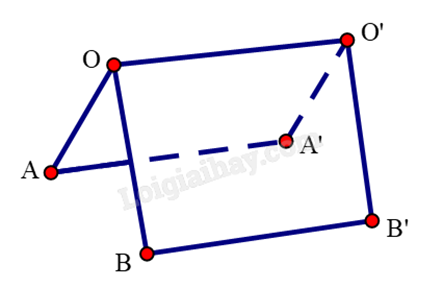
Giả sử hai mái ngói là hai hình chữ nhật OAA’O’ và OBB’O’. Khi đó:
\(\left\{ \begin{array}{l}\left( {OAA'O'} \right) \cap \left( {OBB'O'} \right) = OO'\\OA \bot OO',\,OA \subset \left( {OAA'O'} \right)\\OB \bot OO',\,OB \subset \left( {OBB'O'} \right)\end{array} \right.\) nên \(\widehat {AOB}\) là góc phẳng nhị diện \(\left[ {A,OO',B} \right]\). Vậy \(\widehat {AOB} = \alpha \).
Áp dụng định lý cosin cho tam giác OAB ta được:
\(\cos \widehat {AOB} = \cos \alpha = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{2,{2^2} + {3^2} - 3,{8^2}}}{{2.2,2.3}} = - \frac{1}{{22}} = \frac{m}{n}\)\( \Rightarrow m = - 1;n = 22\).
Vậy \(3m + {n^2} = - 3 + 484 = 481\).
Trong phép thử T, cho A và B là hai biến cố độc lập nhau. Biết P(A) + P(B) = 1,1 và P(AB) = 0,3. Tính xác suất của biến cố \(\overline A .\overline B \).
Đáp án:
Đáp án:
Áp dụng quy tắc nhân xác suất cho hai biến cố độc lập, công thức tính xác suất của biến cố đối.
Ta có \(P\left( {AB} \right) = 0,3 \Rightarrow P\left( A \right).P\left( B \right) = 0,3\) (vì A và B độc lập). Suy ra ta có hệ:
\(\left\{ \begin{array}{l}P\left( A \right) + P\left( B \right) = 1,1\\P\left( A \right).P\left( B \right) = 0,3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}P\left( A \right) = 0,5 \Rightarrow P\left( {\overline A } \right) = 0,5\\P\left( B \right) = 0,6 \Rightarrow P\left( {\overline B } \right) = 0,4\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}P\left( A \right) = 0,6 \Rightarrow P\left( {\overline A } \right) = 0,4\\P\left( B \right) = 0,5 \Rightarrow P\left( {\overline B } \right) = 0,5\end{array} \right.\).
Lại có A và B là hai biến cố độc lập nên \(\overline A \) và \(\overline B \) cũng độc lập.
Do đó \(P\left( {\overline A .\overline B } \right) = P\left( {\overline A } \right).P\left( {\overline B } \right) = 0,5.0,4 = 0,4.0,5 = 0,2\).
Một tháp trung tâm kiểm soát không lưu ở sân bay cao 80 m sử dụng ra đa có phạm vi theo dõi 500 km được đặt trên đỉnh tháp. Chọn hệ trục toạ độ Oxyz có gốc O trùng với vị trí chân tháp, mặt phẳng (Oxy) trùng với mặt đất sao cho trục Ox hướng về phía tây, trục Oy hướng về phía nam, trục Oz hướng thẳng đứng lên phía trên (đơn vị trên mỗi trục tính theo kilômét).

Một máy bay tại vị trí A cách mặt đất 10 km, cách 300 km về phía đông và 200 km về phía bắc so với tháp trung tâm kiểm soát không lưu. Khoảng cách từ máy bay đến ra đa bằng bao nhiêu ki-lô-mét (làm tròn kết quả đến hàng đơn vị)?
Đáp án:
Đáp án:
Xác định tọa độ ra đa và máy bay dựa vào dữ liệu đề bài cho. Áp dụng công thức tính khoảng cách giữa hai điểm.
Đổi 80 m = 0,08 km.
Theo giả thiết, ra đa ở vị trí có toạ độ (0;0;0,08), máy bay ở vị trí có tọa độ A(-300;-200;10).
Vậy khoảng cách từ máy bay đến ra đa là: \(\sqrt {{{( - 300 - 0)}^2} + {{( - 200 - 0)}^2} + {{(10 - 0,08)}^2}} \approx 361\) (km).
Một ngọn hải đăng được đặt tại vị trí A cách bờ biển một khoảng AB = 5 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng 7 km. Người canh hải đăng có thể chèo đò từ A đến địa điểm M trên bờ biển với vận tốc 4 km/h, rồi đi bộ đến C với vận tốc 6 km/h.

Vị trí của M cách B một khoảng bằng bao nhiêu ki-lô-mét thì người canh hải đăng đến kho nhanh nhất (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Đáp án:
Đặt BM = x. Lập hàm số biểu diễn thời gian người canh hải đăng đến kho rồi tìm x để hàm số đạt giá trị nhỏ nhất.
Gọi BM = x (km, \(0 \le x \le 7\)).\(\)
Khi đó \(AM = \sqrt {{x^2} + 25} \) (km).
Thời gian người đó đi từ A đến M rồi đến C là \(f\left( x \right) = \frac{{\sqrt {{x^2} + 25} }}{4} + \frac{{7 - x}}{6}\) (giờ).
Ta có: \(f'\left( x \right) = \frac{x}{{4\sqrt {{x^2} + 25} }} - \frac{1}{6}\) .
Xét \(f'\left( x \right) = 0 \Leftrightarrow 6x = 4\sqrt {{x^2} + 25} \)\( \Leftrightarrow x = 2\sqrt 5 \in \left[ {0;7} \right]\).
\(f\left( 0 \right) = \frac{{29}}{{12}}\), \(f\left( 7 \right) = \frac{{\sqrt {74} }}{4}\), \(f\left( {2\sqrt 5 } \right) = \frac{{5\sqrt 5 }}{{12}} + \frac{7}{6}\).
Vậy để đến kho nhanh nhất thì \(x = 2\sqrt 5 \approx 4,47\) (km).
Một tấm bạt hình vuông cạnh 20 m như hình vẽ dưới đây. Người ta dự tính cắt phần tô đậm của tấm bạt rồi gập và may lại (các đường may không đáng kể), nhằm mục đích phủ lên tháp đèn trang trí (tháp dạng hình chóp tứ giác đều) để tránh hư hại tháp khi trời mưa.

Biết khối chóp hình thành sau khi gập và may lại cần thể tích lớn nhất thì mới phủ kín tháp đèn. Hỏi phần diện tích tấm bạt bị cắt là bao nhiêu để đảm bảo yêu cầu trên?
Đáp án:
Đáp án:
Lập hàm số biểu diễn thể tích khối chóp theo ẩn x. Tìm x để thể tích khối chóp lớn nhất bằng cách ứng dụng đạo hàm, từ đó tính diện tích phần bạt bị cắt.
Ta kí hiệu các điểm như trong hình vẽ.
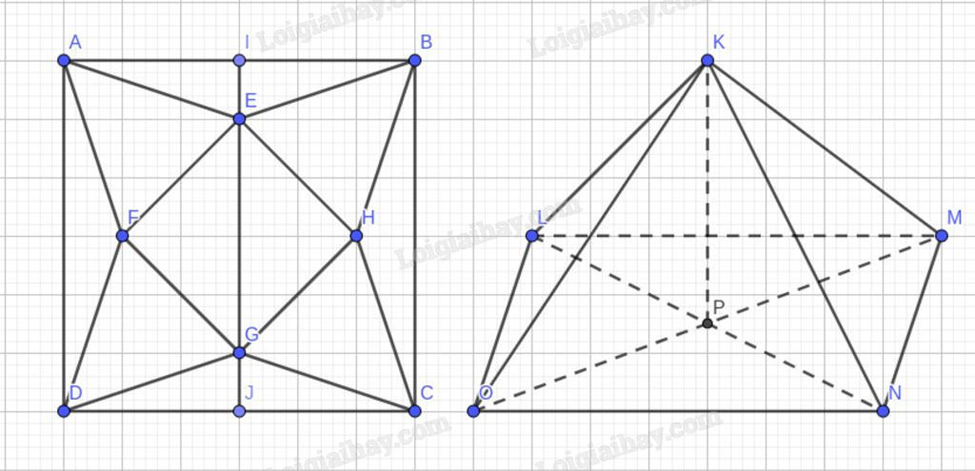
Có \(AI = IB = \frac{{AB}}{2} = \frac{{20}}{2} = 10\) (m), IJ = BC = 20 (m).
Đặt \(EF = FG = GH = HE = x\) (m, x > 0).
\(FH = EG = \sqrt {E{H^2} + H{G^2}} = \sqrt {{x^2} + {x^2}} = x\sqrt 2 \) (m).
\(EI = GJ = \frac{{IJ - EG}}{2} = \frac{{20 - x\sqrt 2 }}{2}\) (m).
Xét tam giác AIE vuông tại I:
\(AE = \sqrt {A{I^2} + I{E^2}} = \sqrt {{{10}^2} + {{\left( {\frac{{20 - x\sqrt 2 }}{2}} \right)}^2}} = \sqrt {\frac{{{x^2}}}{2} - 10\sqrt 2 x + 200} \) (m).
\(LN = OM = EG = HF = x\sqrt 2 \) (m), \(LP = \frac{{LN}}{2} = \frac{{x\sqrt 2 }}{2}\) (m).
\(KL = KO = KM = KN = AE = \sqrt {\frac{{{x^2}}}{2} - 10\sqrt 2 x + 200} \) (m).
Xét tam giác KLP vuông tại P:
\(KP = \sqrt {K{L^2} - L{P^2}} = \sqrt {\frac{{{x^2}}}{2} - 10\sqrt 2 x + 200 - \frac{{{x^2}}}{2}} = \sqrt {200 - 10\sqrt 2 x} \) (m).
Điều kiện: \(x \le 10\sqrt 2 \).
Thể tích khối chóp là:
\(V = \frac{1}{3}.KP.{S_{LMNO}} = \frac{1}{3}.\sqrt {200 - 10\sqrt 2 x} .{x^2}\) \(\left( {{m^3}} \right)\).
Đặt \(y = \frac{1}{3}.\sqrt {200 - 10\sqrt 2 x} .{x^2}\), ta có \(y' = \frac{{ - 25\sqrt 2 {x^2} + 400x}}{{3\sqrt {200 - 10\sqrt 2 x} }} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 8\sqrt 2 \end{array} \right.\) (loại x = 0).
Bảng biến thiên:
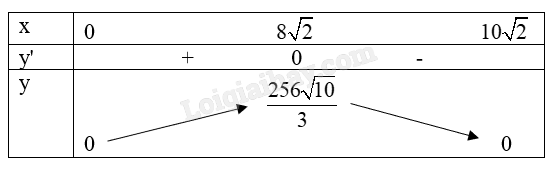
Vậy thể tích khối chóp lớn nhất khi \(x = 8\sqrt 2 \) (m).
Diện tích tấm bạt bị cắt khi đó là \(S = 4{S_{AEB}} = 4.\frac{1}{2}.EI.AB = 2.\frac{{20 - 8\sqrt 2 .\sqrt 2 }}{2}.20 = 80\) \(\left( {{m^2}} \right)\).
Biết hình phẳng (H) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có trục đối xứng vuông góc với trục hoành. Tính diện tích phần kẻ hình ca-rô của hình vẽ (kết quả làm tròn đến hàng phần trăm).

Đáp án:
Đáp án:
Dựa vào phương trình hoành độ giao điểm của (C) và (P) để tìm hệ số a của phương trình hoành độ giao điểm. Từ đó, áp dụng công thức tính diện tích hình phẳng ứng dụng tích phân.
Dựa vào đồ thị hàm số đề bài cho ta có:
Parabol (P) đi qua gốc toạ độ O nên hàm số bậc hai có dạng \(f\left( x \right) = m{x^2} + nx\).
Xét hàm số bậc ba \(g\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị (C), vì đồ thị (C) đi qua điểm (0;2) nên d = 2.
Xét phương trình hoành độ giao điểm của (C) và (P):
\(g\left( x \right) = f\left( x \right) \Leftrightarrow a\left( {x + 2} \right)\left( {{x^2} - 1} \right) = 0\).
Mặt khác \(g\left( x \right) = f\left( x \right) \Leftrightarrow a{x^3} + b{x^2} + cx + 2 = m{x^2} + nx \Leftrightarrow a{x^3} + \left( {b - m} \right){x^2} + \left( {c - n} \right)x + 2 = 0\).
Nên ta có hệ số tự do \( - 2a = 2 \Leftrightarrow a = - 1\).
Do đó \(g\left( x \right) - f\left( x \right) = - \left( {x + 2} \right)\left( {{x^2} - 1} \right)\).
\(S = \int\limits_{ - 2}^1 {\left| {g\left( x \right) - f\left( x \right)} \right|{\rm{d}}x} = \int\limits_{ - 2}^1 {\left| { - \left( {x + 2} \right)\left( {{x^2} - 1} \right)} \right|{\rm{d}}x} \approx 3,08\).
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Các bài khác cùng chuyên mục
- Đề thi thử THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
- Đề thi THPT môn Toán năm 2025 (Mã 123) có lời giải
- Đề tham khảo thi THPT môn Toán - Đề số 10 (hay, chi tiết)
- Đề khảo sát chất lượng Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội
- Đề thi thử THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
- Đề thi THPT môn Toán năm 2025 (Mã 123) có lời giải
- Đề tham khảo thi THPT môn Toán - Đề số 10 (hay, chi tiết)
- Đề khảo sát chất lượng Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội








