Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1 m. Một ô tô A đang chạy với vận tốc 16 m/s thì gặp ô tô B đang dừng đèn đỏ nên ô tô A hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức \({v_A}(t) = 16 - 4t\) (đơn vị tính bằng m/s, thời gian t tính bằng giây).
a) Thời điểm xe ô tô A dừng lại là 4 giây kể từ lúc hãm phanh.
b) Quãng đường S(t) (đơn vị: mét) mà ô tô A đi được trong thời gian t giây \((0 \le t \le 4)\) kể từ khi hãm phanh được tính theo công thức \(S(t) = \int\limits_0^4 {v(t)dt} \).
c) Từ khi bắt đầu hãm phanh đến khi dừng lại, xe tô tô A đi được quãng đường 32 m.
d) Khoảng cách an toàn tối thiểu giữa ô tô A và ô tô B trước khi ô tô A hãm phanh là 37 m.
a) Thời điểm xe ô tô A dừng lại là 4 giây kể từ lúc hãm phanh.
b) Quãng đường S(t) (đơn vị: mét) mà ô tô A đi được trong thời gian t giây \((0 \le t \le 4)\) kể từ khi hãm phanh được tính theo công thức \(S(t) = \int\limits_0^4 {v(t)dt} \).
c) Từ khi bắt đầu hãm phanh đến khi dừng lại, xe tô tô A đi được quãng đường 32 m.
d) Khoảng cách an toàn tối thiểu giữa ô tô A và ô tô B trước khi ô tô A hãm phanh là 37 m.
a) Khi xe ô tô dừng hẳn thì \({v_A}(t) = 0\). Giải phương trình tìm t.
b, c) Sử dụng công thức \(S(t) = \int\limits_0^t {v(t)dt} \).
d) Khoảng cách an toàn tối thiểu giữa ô tô A và ô tô B trước khi ô tô A hãm phanh bằng tổng quãng đường ô tô A di chuyển từ lúc hãm phanh đến khi dừng hẳn và khoảng cách tối thiểu khi dừng đèn đỏ.
a) Đúng. Khi ô tô A dừng lại thì \({v_A}(t) = 0 \Leftrightarrow 16 - 4t = 0 \Leftrightarrow t = 4\).
b) Sai. Quãng đường S(t) ô tô đi được trong thời gian t giây \((0 \le t \le 4)\) được tính theo công thức \(S(t) = \int\limits_0^t {v(t)dt} \).
c) Đúng. Quãng đường xe tô tô A đi được kể từ lúc hãm phanh đến khi dừng hẳn là \(S(t) = \int\limits_0^4 {(16 - 4t)dt} = 32\) (m).
d) Sai. Để đảm bảo khoảng cách an toàn tối thiểu 1 m khi dừng lại, ô tô A phải bắt đầu hãm phanh khi cách ô tô B ít nhất 32 + 1 = 33 (m).

Các bài tập cùng chuyên đề
Biết \(F(x) = {x^3}\) là một nguyên hàm của hàm số f(x) trên \(\mathbb{R}\). Giá trị của \(\int\limits_1^2 {[2 + f(x)]dx} \) bằng:
A. \(\frac{{23}}{4}\)
B. 7
C. 9
D. \(\frac{{15}}{4}\)
Biết \(\int\limits_0^1 {[f(x) + 2x]dx = 2} \). Khi đó, \(\int\limits_0^1 {f(x)dx} \) bằng:
A. 1
B. 4
C. 2
D. 0
Tìm
a) \(\int {2x({x^3}} - x + 2)dx\)
b) \(\int {\left( {2x + \frac{1}{{{x^3}}}} \right)} dx\)
c) \(\int {\left( {3 + 2{{\tan }^2}x} \right)} dx\)
d) \(\int {\left( {1 - 3{{\cot }^2}x} \right)} dx\)
e) \(\int {\left( {\sin + {2^{ - x + 1}}} \right)} dx\)
g) \(\int {\left( {{{2.6}^{2x}} - {e^{ - x + 1}}} \right)} dx\)
Tính
a) \(\int\limits_{ - 1}^1 {{{(x + 2)}^3}} dx\)
b) \(\int\limits_1^2 {\frac{2}{{{x^2}}}} dx\)
c) \(\int\limits_1^4 {{x^2}\sqrt x } dx\)
d) \(\int\limits_{ - 1}^0 {{2^{3x + 2}}} dx\)
e) \(\int\limits_0^2 {{2^x}{{.3}^{x + 1}}} dx\)
g) \(\int\limits_0^1 {\frac{{{7^x}}}{{{{11}^x}}}} dx\)
Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm t là h(t), trong đó t tính bằng phút, h(t) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số \(v(t) = - 0,12{t^2} + 1,2t\) với t tính bằng phút, v(t) tính bằng mét/ phút. Tại thời điểm xuất phát (t=0), khinh khí cầu ở độ cao 520m và 5 phút sau khi xuất phát (t = 0), khinh khí cầu ở độ cao 520m và 5 phút sau khi xuất phát, khinh khí cầu đã ở độ cao 530m
a) Viết công thức xác định hàm số h(t) \((0 \le t \le 29)\)
b) Độ cao tối đa của khinh khí cầu khi bay là bao nhiêu?
c) Khi nào khinh khí cầu sẽ trở lại độ cao khi xuất phát?
Một công trình xây dựng dự kiến hoàn thành trong 100 ngày. Số lượng công nhân được sử dụng tại thời điểm t cho bởi hàm số \(m(t) = 500 + 50\sqrt t - 10t\), trong đó t tính theo ngày , m(t) tính theo người
a) Khi nào có 360 công nhân được sử dụng?
b) Khi nào số công nhân được sử dụng lớn nhất?
c) Gọi M(t) là số ngày công được tính đến hết ngày thứ t (kể từ khi khởi công công trình). Trong kinh tế xây dựng, người ta đã biết rằng M’(t) = m(t). Tổng cộng cần bao nhiêu ngày công để hoàn thành công trình xây dựng đó?
Trong bài này, ta xét một tình huống giả định có một học sinh sau kỳ nghỉ đã mang virus cúm quay trở lại khuôn viên trường học biệt lập. Sau khi có sự tiếp xúc giữa các học sinh, virus cúm lây lan trong khuôn viên trường. Giả thiết hệ thống chống dịch chưa được khởi động và virus cúm được lây lan tự nhiên. Gọi P(t) là số học sinh bị nhiễm virus cúm ở ngày thứ t tính từ ngày học sinh mang virus cúm quay trở lại khuôn viên trường. Biết rằng tốc độ lây lan của virus cúm cho bởi công thức \(P'(t) = - 0,02C{e^{ - 0,02t}}\), trong đó C là hằng số khác 0. Số học sinh bị nhiễm virus cúm sau 4 ngày là 55 học sinh. Xác định số học sinh bị nhiễm virus cúm sau 10 ngày.
Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên. Tốc độ của chiếc xe ô tô đó (tính bằng mét/giây) lần lượt ở giây thứ 10, thứ 20, thứ 30, thứ 40, thứ 50 và thứ 60 được ghi lại trong Bảng 1.
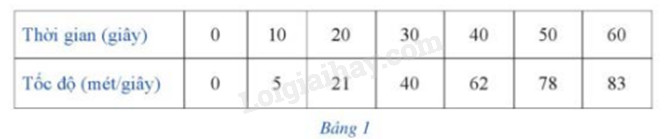
a) Hãy xây dựng hàm số bậc ba \(y = f(x) = a{x^3} + b{x^2} + cx + d(a \ne 0)\) để biểu diễn các số liệu ở Bảng 1, tức là ở hệ trục tọa độ Oxy, đồ thị của hàm số đó trên nửa khoảng \([0; + \infty )\) “gần” với các điểm O(0;0), B(10;5), C(20;21), D(30;40), E(40;62), G(50;78), K(60;83).
b) Hãy tính (gần đúng) quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm.
Tính các tích phân sau:
a) \(\int\limits_{ - 2}^4 {\left( {x + 1} \right)\left( {x - 1} \right)dx} \)
b) \(\int\limits_1^2 {\frac{{{x^2} - 2x + 1}}{x}dx} \)
c) \(\int\limits_0^{\frac{\pi }{2}} {\left( {3\sin x - 2} \right)dx} \)
d) \(\int\limits_0^{\frac{\pi }{2}} {\frac{{{{\sin }^2}x}}{{1 + \cos x}}dx} \)
Tính các tích phân sau:
a) \(\int\limits_{ - 2}^1 {\left| {2x + 2} \right|dx} \)
b) \(\int\limits_0^4 {\left| {{x^2} - 4} \right|dx} \)
c) \(\int\limits_{ - \frac{\pi }{2}}^{\frac{\pi }{2}} {\left| {\sin x} \right|dx} \)
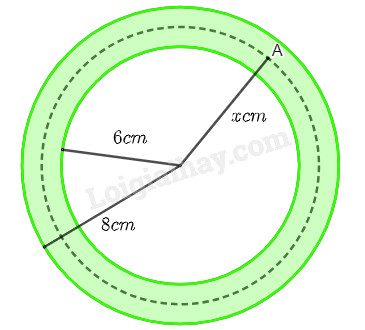
Mặt cắt ngang của một ống dẫn khí nóng là một hình vành khuyên như hình dưới đây. Khí bên trong ống được duy trì ở \({150^o}{\rm{C}}\). Biết rằng nhiệt độ \(T\left( {^oC} \right)\) tại điểm A trên thành ống là hàm số của khoảng cách \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) từ A đến tâm của mặt cắt và \(T'\left( x \right) = - \frac{{30}}{x}\) \(\left( {6 \le x \le 8} \right)\). Tìm nhiệt độ mặt ngoài của ống.
Tốc độ \(v{\rm{ }}\left( {{\rm{m/s}}} \right)\) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian \(t\) (giây) được cho bởi công thức \(v\left( t \right) = \left\{ {\begin{array}{*{20}{c}}t&{\left( {0 \le t \le 2} \right)}\\2&{\left( {2 < t \le 20} \right)}\\{12 - 0,5t}&{\left( {20 < t \le 24} \right)}\end{array}} \right.\). Tính quãng đường chuyển động và tốc độ trung bình của thang máy.
Giá trị của \(\int\limits_{ - 2}^1 {\left( {4{x^3} + 3{x^2} + 8x} \right)dx} + \int\limits_1^2 {\left( {4{x^3} + 3{x^2} + 8x} \right)dx} \) bằng
A. \(16\)
B. \( - 16\)
C. \(52\)
D. \(0\)
Giá trị của \(\int\limits_0^2 {\left| {{x^2} - x} \right|dx} \) bằng:
A. \(\frac{2}{3}\)
B. \(1\)
C. \(\frac{1}{3}\)
D. \(2\)
Tính các tích phân sau:
a) \(\int\limits_0^1 {\left( {4{x^3} + x} \right)dx} \)
b) \(\int\limits_1^2 {\frac{{x - 2}}{{{x^2}}}dx} \)
c) \(\int\limits_0^4 {{2^{2x}}dx} \)
d) \(\int\limits_1^2 {\left( {{e^{x - 1}} + {2^{x + 1}}} \right)dx} \)
Tính các tích phân sau: a) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{4}} {\frac{1}{{{{\sin }^2}x}}dx} \) b) \(\int\limits_0^{\frac{\pi }{4}} {\left( {1 + \tan x} \right)\cos xdx} \)
Một vật chuyển động với tốc độ \(v\left( t \right) = 3t + 4{\rm{ }}\left( {{\rm{m/s}}} \right)\), với thời gian \(t\) tính theo giây, \(t \in \left[ {0;5} \right]\). Tính quãng đường vật đi được trong khoảng thời gian từ \(t = 0\) đến \(t = 5\).
Lợi nhuận biên của một sản phẩm được mô hình hóa bởi
\(P'\left( x \right) = - 0,0005x + 12,2\).
a) Tìm sự thay đổi lợi nhuận khi doanh số bán hàng tăng từ 100 lên 101 đơn vị.
b) Tìm sự thay đổi lợi nhuận khi doanh số bán hàng tăng từ 100 lên 110 đơn vị.
Tìm chi phí trung bình trên mỗi đơn vị sản phẩm trong khoảng thời gian thời gian hai năm nếu chi phí cho mỗi đơn vị được tính bởi \(c\left( t \right) = 0,005{t^2} + 0,02t + 12,5\) với \(0 \le t \le 24\), tính theo tháng.
Giả sử tổng chi phí mua và bảo trì một thiết bị trong x năm có thể được mô hình hóa bởi công thức
\(C = 5000\left( {25 + 3\int\limits_0^x {{t^{\frac{1}{4}}}dt} } \right)\).
Tìm tổng chi phí sau:
a) 1 năm;
b) 5 năm;
c) 10 năm.
Vận tốc \(v\) của một vật rơi tự do từ trạng thái đứng yên được cho bởi công thức
\(v\left( t \right) = 9,8t\), trong đó vận tốc \(v\) tính bằng m/s và thời gian t tính bằng giây.
a) Biểu thị quãng đường vật đi được trong T giây đầu tiên dưới dạng tích phân.
b) Tìm quãng đường vật đi được trong 5 giây đầu tiên.
Hàm cầu và hàm cung của một sản phẩm được mô hình hóa bởi:
Hàm cầu: \(p = - 0,2x + 8\) và hàm cung: \(p = 0,1x + 2\), trong đó \(x\) là số đơn vị sản phẩm, \(p\) là giá của mỗi đơn vị sản phẩm (tính bằng triệu đồng). Tìm thặng dư tiêu dùng và thặng dư sản xuất đối với sản phẩm này.
Chi phí nhiên liệu dự kiến C (tính bằng triệu đô la mỗi năm) khi sử dụng một loại xe tải của một công ty vận tải từ năm 2020 đến năm 2030 là \({C_1} = 5,6 + 2,2t,{\rm{ }}0 \le t \le 10\), trong đó \(t = 0\) tương ứng với năm 2020. Nếu công ty sử dụng một loại xe tải khác có động cơ hiệu quả hơn thì chi phí nhiên liệu dự kiến sẽ giảm và tuân theo mô hình \({C_2} = 4,7 + 2,04t,{\rm{ }}0 \le t \le 10\). Công ty có thể tiết kiệm được bao nhiêu khi sử dụng xe tải với động cơ hiệu quả hơn?
Doanh thu từ một quy trình sản xuất (tính bằng triệu đô la mỗi năm) được dự kiến sẽ tuân theo mô hình \(R = 100 + 0,08t\) trong 10 năm. Trong cùng khoảng thời gian đó, chi phí (tính bằng triệu đô la mỗi năm) được dự kiến sẽ tuân theo mô hình \(C = 60 + 0,2{t^2}\), trong đó t là thời gian (tính bằng năm).
Ước tính lợi nhuận trong khoảng thời gian 10 năm.
Một trận dịch lây lan đến mức sau khi bùng phát t tuần số người nhiễm bệnh là
\({N_1}\left( t \right) = 0,1{t^2} + 0,5t + 150,0 \le t \le 50\).
Hai mươi lăm tuần sau khi dịch bệnh bùng phát, một loại vắc xin đã được phát triển và tiêm cho công chúng. Khi đó, số người nhiễm bệnh được điều chỉnh theo mô hình
\({N_2}\left( t \right) = - 0,2{t^2} + 6t + 200,25 \le t \le 50\).
a) Tìm thời điểm t để sau khi tiêm vắc xin thì dịch bệnh kết thúc, tức là số người nhiễm bệnh là \({N_2}\left( t \right) = 0\).
b) Ước tính gần đúng số người mà vắc xin đã ngăn ngừa khỏi dịch bệnh trong thời gian xảy ra dịch bệnh.
Giá trị trung bình của hàm \(f\left( x \right)\) trên \(\left[ {a;b} \right]\) được tính theo công thức \(m = \frac{1}{{b - a}}\int\limits_a^b {f\left( x \right)dx} \). Khi đó giá trị trung bình của hàm \(f\left( x \right) = {x^2} + 2x\) trên đoạn \(\left[ {0;3} \right]\) là
A. \(\frac{8}{3}\).
B. 18.
C. 6.
D. 5.
Một đất nước tiêu thụ dầu theo tốc độ xác định bởi \(r\left( t \right) = 20 \cdot {e^{0,2t}}\) tỉ thùng mỗi năm, trong đó t là thời gian tính theo năm, \(0 \le t \le 10\). Trong khoảng 10 năm kể trên, nước đó đã tiêu thụ lượng dầu là
A. \(r\left( {10} \right)\).
B. \(r\left( {10} \right) - r\left( 0 \right)\).
C. \(\int\limits_0^{10} {r'\left( t \right)dt} \).
D. \(\int\limits_0^{10} {r\left( t \right)dt} \).
Khi nghiên cứu một quần thể vi khuẩn, người ta nhận thấy quần thể vi khuẩn đó ở ngày thứ t có số lượng \(N\left( t \right)\) con. Biết rằng tốc độ phát triển của quần thể đó là \(N'\left( t \right) = \frac{{8000}}{t}\) và sau ngày thứ nhất \(\left( {t = 1} \right)\) có 250 000 con. Sau 6 ngày \(\left( {t = 6} \right)\), số lượng của quần thể vi khuẩn là
A. 353 584 con.
B. 234 167 con.
C. 288 959 con.
D. 264 334 con.
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để \(\int\limits_0^3 {\left( {10x - 2m} \right)dx} > 0\)
Khi nghiên cứu dịch sốt xuất huyết ở một địa phương, các chuyên gia y tế ước tính rằng tại ngày thứ \(m\) có \(F\left( m \right)\) người mắc bệnh (sau khi đã làm tròn đến chữ số hàng đơn vị). Biết rằng tốc độ lan truyền bệnh là \(F'\left( m \right) = \frac{{150}}{{2m + 1}}\) và ngày đầu tiên \(\left( {m = 0} \right)\) người ta phát hiện ra 50 bệnh nhân. Hãy xác định biểu thức của \(F\left( m \right)\) và số người mắc bệnh ở ngày thứ 10.






