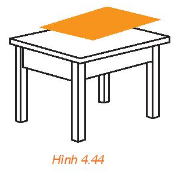
Cho hình hộp ABCD.A’B’C’D’. Mệnh đề nào dưới đây là sai?
-
A.
(ADD’A’) // (BCC’B’)
-
B.
(BDA’) // (B’D’C)
-
C.
(ABA’) // (B’D’C)
-
D.
(ABCD) // (A’B’C’D’)
Hai mặt phẳng song song với nhau nếu một mặt phẳng chứa hai đường thẳng cắt nhau song song với mặt phẳng còn lại.
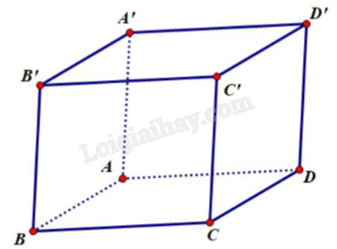
Dễ thấy các mệnh đề ở đáp án A, D đúng (hai mặt phẳng đối diện của hình hộp song song với nhau).
Xét đáp án B: \(\left\{ \begin{array}{l}BD//B'D' \Rightarrow BD//(B'D'C)\\A'B//D'C \Rightarrow A'B//(B'D'C)\\A'B \cap BD = \{ B\} \end{array} \right. \Rightarrow (BDA')//(B'D'C)\).
Vậy mệnh đề đáp án B đúng.
Xét đáp án C: (ABA’) chính là (ABB’A’). Mà (ABB’A’) giao (B’D’C) tại B’ nên hai mặt phẳng này không song song với nhau.
Vậy mệnh đề đáp án C sai.
Đáp án : C

Các bài tập cùng chuyên đề
Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD).
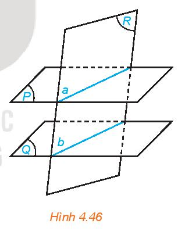
Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46)
a) Giải thích vì sao mặt phẳng (R) cắt mặt phẳng (Q).
b) Gọi b là giao tuyến của hai mặt phẳng (R) và (Q). Hai đường thẳng a và b có thể chéo nhau hay không, có thể cắt nhau hay không?
Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là các điểm thuộc các cạnh SA, SB, SC, SD sao cho
\(\frac{{MA}}{{MS}} = \frac{{NB}}{{NS}} = \frac{{PC}}{{PS}} = \frac{{QD}}{{QS}} = \frac{1}{2}\). Chứng minh rẳng bốn điểm M, N, P, Q đồng phẳng.
Đặt một tấm bìa cứng lên một góc của mặt bàn nằm ngang (H.4.44) sao cho mặt bìa song song với mặt đất. Khi đó mặt bìa có trùng với mặt bàn hay không?
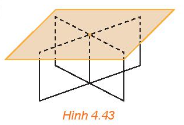
Một chiếc bàn có phần chân là hai khung sắt hình chữ nhật có thể xoay quanh một trục như trong Hình 4.43. Khi mặt bàn được đặt lên phần chân bàn thì mặt bàn luôn song song với mặt đất. Hãy giải thích tại sao.
Trong không gian, cho bốn điểm A, B, C, D không đồng phẳng. Qua điểm A vẽ hai đường thẳng m; n lần lượt song song với hai đường thẳng BC, BD. Chứng minh rằng mp(m, n) song song với mặt phẳng (BCD)
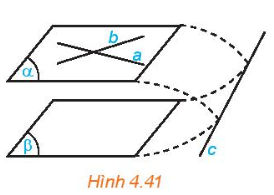
Cho mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng \(\left( \beta \right)\) (H.4.41)
Nếu \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không?
Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.
Trong không gian cho ba mặt phẳng phân biệt (P), (Q), (R). Những mệnh đề nào sau đây là đúng?
a) Nếu (P) chứa một đường thẳng song song với (Q) thì (P) song song với (Q).
b) Nếu (P) chứa hai đường thẳng song song với (Q) thì (P) song song với (Q).
c) Nếu (P) và (Q) song song với (R) thì (P) song song với (Q).
d) Nếu (P) và (Q) cắt (R) thì (P) và (Q) song song với nhau.
Cho hình thang ABCD có hai đáy AB và CD. Qua các điểm A, D lần lượt vẽ các đường thẳng m, n song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh rằng mp(B,m) và mp(C,n) song song với nhau.
Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (AB’D’) song song với mặt phẳng
A. (ABCD)
B. (BCC’B’)
C. (BDA’)
D. (BDC’)
Cho mặt phẳng (Q) và điểm M nằm ngoài mặt phẳng (Q).
a) Trong mặt phẳng (Q) vẽ hai đường thẳng a’, b’ cắt nhau. Qua điểm M kẻ các đường thẳng a, và b lần lượt song song với a’, b’. Gọi (P) là mặt phẳng xác định bởi hai đường thẳng (cắt nhau) a và b (Hình 63). Mặt phẳng (P) có song song với mặt phẳng (Q) hay không?
b) Xét mặt phẳng (R) đi qua điểm M và song song với mặt phẳng (Q). Hai mặt phẳng (R) và (P) có trùng nhau hay không?

Cho tứ diện ABCD. Các điểm M, N, P, I, J, K lần lượt là trung điểm của BC, CD, DB, AM, AN, AP. Chứng minh rằng (IJK) // (BCD).
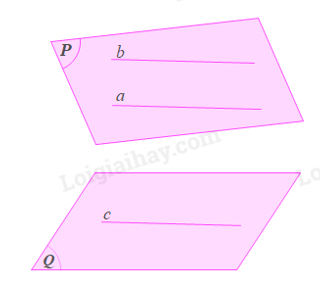
Cho hai mặt phẳng phân biệt (P) và (Q). Mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và a, b cùng song song với mặt phẳng (Q) (Hình 61). Hai mặt phẳng (P) và (Q) có điểm chung hay không?

Bạn Chung cho rằng: Nếu mặt phẳng (P) chứa hai đường thẳng a, b và a, b cùng song song với mặt phẳng (Q) thì (P) luôn song song với (Q). Phát biểu của bạn Chung có đúng không? Vì sao?
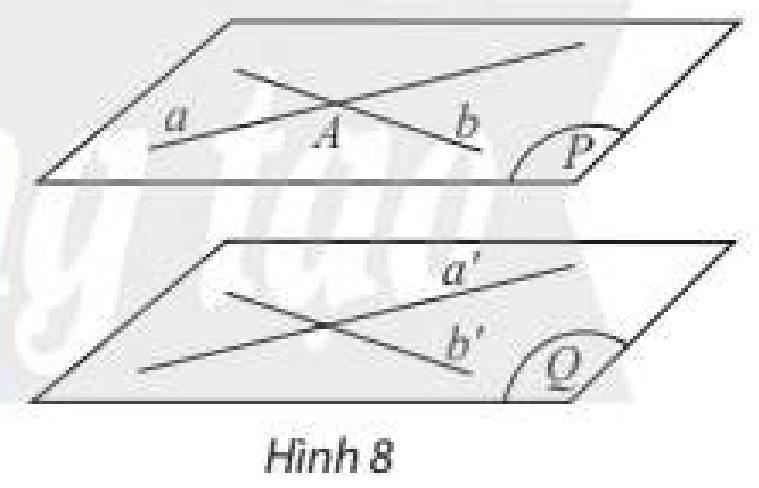
Trong không gian, hai mặt phẳng song song với nhau khi và chỉ khi:
A. Có một mặt phẳng chứa hai đường thẳng phân biệt cùng song song với mặt phẳng còn lại.
B. Hai mặt phẳng cùng song song với một đường thẳng
C. Hai mặt phẳng cùng song song với mặt phẳng thứ ba
D. Hai mặt phẳng không có điểm chung
Cho tứ diện \(ABCD\) có \(E,F,H\)lần lượt là trung điểm của \(AB,AC,AD\). Chứng minh \(\left( {EFH} \right)\parallel \left( {BCD} \right)\).
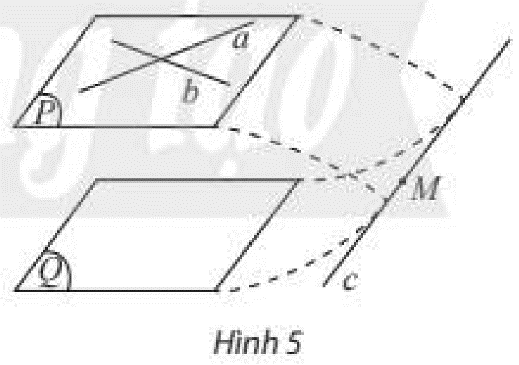
Cho mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và cùng song song với mặt phẳng \(\left( Q \right)\). Giả sử \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung \(M\) thì \(\left( P \right)\) cắt \(\left( Q \right)\) theo giao tuyến \(c\) (Hình 5).
a) Giải thích tại sao đường thẳng \(c\) phải cắt ít nhất một trong hai đường thẳng \(a,b\). Điều này có trái với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\) không?
b) Rút ra kết luận về số điểm chung và vị trí tương đối của \(\left( P \right)\) và \(\left( Q \right)\).
Khi dùng dao cắt các lớp bánh (Hình 11), giả sử bề mặt của các lớp bánh là các mặt phẳng song song và con dao được xem như mặt phẳng \(\left( P \right)\), nêu kết luận về các giao tuyến tạo bởi \(\left( P \right)\) với các bể mặt của các lớp bánh. Giải thích.

Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình bình hành có \(O\) là giao điểm của hai đường chéo, tam giác \(SBD\) là tam giác đều. Một mặt phẳng \(\left( \alpha \right)\) di động song song với mặt phẳng \(\left( {SBD} \right)\) và cắt đoạn thẳng \(AC\). Chứng minh các giao tuyến của \(\left( \alpha \right)\) với hình chóp tạo thành một tam giác đều.
Cho ba mặt phẳng \(\left( P \right),\left( Q \right),\left( R \right)\) thoả mãn \(\left( P \right)\parallel \left( Q \right)\), \(\left( R \right) \cap \left( P \right) = a\) và \(\left( R \right) \cap \left( Q \right) = b\). Xét vị trí tương đối của \(a\) và \(b\).

a) Cho điểm \(A\) ở ngoài mặt phẳng \(\left( Q \right)\). Trong \(\left( Q \right)\) vẽ hai đường thẳng cắt nhau \(a'\) và \(b'\). Làm thế nào để vẽ hai đường thẳng \(a\) và \(b\) đi qua \(A\) và song song với \(\left( Q \right)\)?
b) Có nhận xét gì về mối liên hệ giữa \(mp\left( {a,b} \right)\)và \(\left( Q \right)\)?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M\), \(N\) lần lượt là trung điểm của \(SA\), \(SC\). Trong các đường thẳng sau, đường thẳng nào song song với \(MN\)?
A. \(AB\)
B. \(AD\)
C. \(BD\)
D. \(AC\)
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(\left( P \right)\)?
A. 0
B. 1
C. 2
D. Vô số
Cho mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right)\). Khẳng định nào sau đây là đúng?
A. Mọi đường thẳng nằm trong \(\left( P \right)\) đều song song với mọi đường thẳng nằm trong \(\left( Q \right)\).
B. \(\left( P \right)\) song song với mọi đường thẳng nằm trong \(\left( Q \right)\).
C. Nếu mặt phẳng \(\left( R \right)\) song song với mặt phẳng \(\left( P \right)\) thì mặt phẳng \(\left( R \right)\) song song với mặt phẳng \(\left( Q \right)\).
D. Nếu đường thẳng \(a\) song song với mặt phẳng \(\left( Q \right)\) thì đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\).
Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình bình hành. Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của \(AB\), \(CD\), \(SA\). Khẳng định nào sau đây là đúng?
A. \(\left( {SBN} \right)\parallel \left( {DAP} \right)\)
B. \(\left( {SBC} \right)\parallel \left( {MPD} \right)\)
C. \(\left( {SBN} \right)\parallel \left( {PMD} \right)\)
D. \(\left( {SDN} \right)\parallel \left( {MAP} \right)\)
Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng phân biệt. Khẳng định nào sau đây là đúng?
A. \(\left( {ADF} \right)\parallel \left( {BCE} \right)\)
B. \(AD\parallel \left( {BEF} \right)\)
C. \(\left( {ABC} \right)\parallel \left( {DEF} \right)\)
D. \(EC\parallel \left( {ABD} \right)\)
Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường a, b, c, d đôi một song song và không nằm trong mặt phẳng (ABCD).
a) Chứng minh rằng hai mặt phẳng mp(a,b) và mp(c,d) song song với nhau.
b) Chứng minh rằng hai mặt phẳng mp(a,d) và mp(b,c) song song với nhau.
c) Một mặt phẳng cắt bốn đường thẳng a, b, c, d lần lượt tại A’, B’, C’, D’. Chứng minh rằng tứ giác A’B’C’D’ là hình bình hành.
Khi cắt một chiếc bánh gato hình hộp, Thúy nhận thấy vết cắt ở mặt trên và mặt dưới của bánh gợi nên hình ảnh về hai đường thẳng song song với nhau. Hỏi nhận xét của Thúy có đúng không? Vì sao?
Nếu mặt phẳng (R) cắt hai mặt phẳng song song (P) và (Q) lần lượt theo hai giao tuyến a và b thì vị trí tương đối giữa hai đường thẳng a và b là
A. song song
B. chéo nhau
C. trùng nhau
D. cắt nhau
Cho hình chóp S. ABCD có đáy là hình thang ABCD, AD//BC, \(AD = 2BC\). Gọi E, F, I lần lượt là trung điểm của các cạnh SA, AD, SD.
a) Chứng minh (BEF)//(SCD) và CI//(BEF).
b) Tìm giao tuyến của hai mặt phẳng (SBC) và (SAD).
c) Tìm giao điểm K của FI với giao tuyến vừa tìm được ở câu b, từ đó chứng minh (SBF)//(KCD).