Giải mục 2 trang 58,59,60 SGK Toán 12 tập 1 - Cánh diều

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 58 SGK Toán 12 Cánh diều

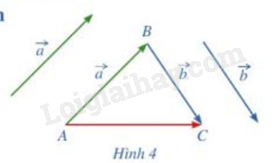
Trong không gian, cho 2 vec tơ \(\vec a\) và \(\vec b\). Lấy một điểm A tùy ý.

a) Vẽ \(\overrightarrow {AB} \)\( = \vec a\),\(\overrightarrow {BC} \)\( = \vec b\)

b) Tổng của 2 vec tơ \(\vec a\)và\(\vec b\) bằng vec tơ nào trong hình 4?

Phương pháp giải:

a) Ghi rõ các bước để vẽ hình

b) Áp dụng quy tắc 3 điểm \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Lời giải chi tiết:

a)

– Qua A vẽ một đường thẳng song song với \(\vec a\). Trên đường thẳng đó lấy điểm B sao cho \(AB = \left| {\vec a} \right|\) và \(\overrightarrow {AB}\) cùng hướng với \({\vec a}\).

– Qua B vẽ một đường thẳng song song với \(\vec b\). Trên đườ ng thẳng đó lấy điểm C sao cho \(BC = \left| {\vec b} \right|\) và \(\overrightarrow {BC}\) cùng hướng với \({\vec b}\).

b) Ta có: \(\vec a + \vec b = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 59 SGK Toán 12 Cánh diều

Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa \(\overrightarrow {AB}  + \overrightarrow {AD} \) và  \(\overrightarrow {AC} ;\;\overrightarrow {AC}  + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \).

Phương pháp giải:

Áp dụng quy tắc ba điểm.

Lời giải chi tiết:

Áp dụng quy tắc ba điểm ta thấy:

\(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {BD} \)               (1)

Mà từ hình vẽ ta thấy  \(\overrightarrow {BD}  = \overrightarrow {AC} \;\;\;\;\;\;\;\;\left( 2 \right)\)

Từ (1) (2) => \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \)

\(\overrightarrow {AC}  + \overrightarrow {AA'}  = \overrightarrow {A'C} \)                  (3)

Mà \(\overrightarrow {A'C}  = \overrightarrow {AC'} \)                     (4)

Từ (3), (4) suy ra \(\overrightarrow {AC}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \)

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 59 SGK Toán 12 Cánh diều

Trong không gian , cho hai vecto\(\;\vec a,\vec b.\;\) Lấy một điểm M tùy ý.

a) Vẽ \(\overrightarrow {MA}  = \vec a,\;\overrightarrow {MB}  = \vec b\;,\overrightarrow {MC}  = \overrightarrow { - b} \).

b) Tổng của hai vecto \(\vec a\;\)và \(\;\overrightarrow { - b} \) bằng vecto nào trong hình 7.

Phương pháp giải:

Sử dụng quy tắc hình bình hành.

Lời giải chi tiết:

\( \vec{a}\) + (\( - \vec{b}) =\) \(\overrightarrow {MA}  + \overrightarrow {MC}  = \overrightarrow {MN} \) (quy tắc hình bình hành).

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 60 SGK Toán 12 Cánh diều

Nêu định nghĩa tích của một số thực \(k \ne 0\;\)với vecto\(\;\vec a\; \ne \vec 0\) trong mặt phẳng.

Lời giải chi tiết:

Cho số thực \(k \ne 0\) và \(vecto\;\vec a \ne \vec 0\). Tích của số k với vecto \(\vec a\) là một vecto, kí hiệu là \(k\vec a,\;\)được xác định như sau:

- Cùng hướng với vecto \(\vec a\) nếu k > 0, ngược hướng với vecto \(\vec a\) nếu k < 0.

- Có độ dài bằng \(\left| k \right|.\left| {\vec a} \right|\).

HĐ6

Trả lời câu hỏi Hoạt động 6 trang 61 SGK Toán 12 Cánh diều

Trong không gian, cho hai vecto \(\vec a,\vec b\)khác \(\;\vec 0\). Lấy một điểm O tùy ý.

a) Vẽ hai vecto \(\overrightarrow {OA}  = \vec a,\;\overrightarrow {OB}  = \vec b\)

b) Khi đó , hai vecto \(\overrightarrow {OA}, \overrightarrow {OB} \) có giá nằm trong cùng mặt phẳng (P) (hình 10). Nếu định nghĩa góc giữa hai vecto \(\overrightarrow {OA}, \;\overrightarrow {OB} \) trong hai mặt phẳng (P).

Lời giải chi tiết:

Trong không gian, cho hai vecto \(\vec a, \vec b\) khác \(\;\vec 0\). Lấy một điểm O tùy ý và vẽ hai vecto\(\;\overrightarrow {OA}  = \vec a,\overrightarrow {OB}  = \vec b\). Góc giữa hai vecto \(\vec a,\overrightarrow {b\;} \) trong không gian, ký hiệu \(\left( {\vec a,\vec b} \right)\) là góc giữa hai vecto \(\;\overrightarrow {OA} ,\overrightarrow {OB} \).

HĐ7

Trả lời câu hỏi Hoạt động 7 trang 61 SGK Toán 12 Cánh diều

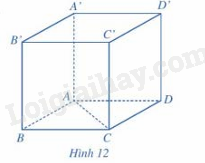
Trong không gian, cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (hình 12).

a) Tính góc giữa hai vecto \(\overrightarrow {AC} ,\overrightarrow {A'D'} \).

b) Tính \(\left| {\overrightarrow {AC} } \right|,\left| {\overrightarrow {A'D'} } \right|\). Cos(\(\overrightarrow {AC} ,\overrightarrow {A'D'} \)).

Phương pháp giải:

Áp dụng quy tắc 3 điểm và vectơ trong không gian.

Lời giải chi tiết:

Ta có A’D’//AD.

Góc giữa \(\overrightarrow {AC} \;\)và\(\;\overrightarrow {A'D'} \)= \(\;\overrightarrow {AC} \) và \(\overrightarrow {AD} \).

a) Mà ABCD là hình vuông => \(\widehat {CAD} = 45^\circ \)

b) \(\overrightarrow {\left| {AC} \right|} .|\overrightarrow {A'D'|} \) = AC.AD = 3.3 = 9.

cos(\(\overrightarrow {AC} ,\overrightarrow {A'D'} \))= cos(\(\overrightarrow {AC} ,\overrightarrow {AD} )\)= \(\frac{{\overrightarrow {AC} .\overrightarrow {AD} }}{{\overrightarrow {\left| {AC} \right|} .\overrightarrow {\left| {AD} \right|} }} = \frac{{3.3}}{{3.3}} = 1\).