 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài 3. Phương trình mặt cầu - Toán 12 Chân trời sáng tạo
Bài 3. Phương trình mặt cầu - Toán 12 Chân trời sáng tạo
Giải mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 - Chân trời sáng tạo
Trong không gian (Oxyz), cho mặt cầu (Sleft( {I;R} right)) có tâm (Ileft( {a;b;c} right)) và bán kính (R). Xét một điểm (Mleft( {x;y;z} right)) thay đổi. a) Tính khoảng cách (IM) theo (x), (y), (z) và (a), (b), (c). b) Nêu điều kiện cần và đủ của (x), (y), (z) để điểm (Mleft( {x;y;z} right)) nằm trên mặt cầu (Sleft( {I;R} right)).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 61 SGK Toán 12 Chân trời sáng tạo
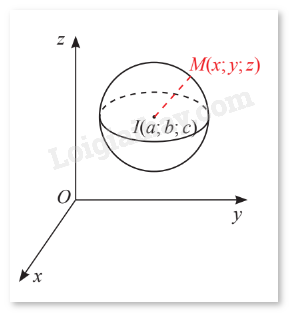
Trong không gian \(Oxyz\), cho mặt cầu \(S\left( {I;R} \right)\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\). Xét một điểm \(M\left( {x;y;z} \right)\) thay đổi.
a) Tính khoảng cách \(IM\) theo \(x\), \(y\), \(z\) và \(a\), \(b\), \(c\).
b) Nêu điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\).
Phương pháp giải:
a) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian để tính khoảng cách \(IM\).
b) Để điểm \(M\) nằm trên mặt cầu \(S\left( {I;R} \right)\) thì \(IM = R\).
Lời giải chi tiết:
a) Ta có \(I\left( {a;b;c} \right)\) và \(M\left( {x;y;z} \right)\). Suy ra \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} \).
b) Điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\) là \(IM = R\), điều này tương đương với
\(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
TH1
Trả lời câu hỏi Thực hành 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Viết phương trình mặt cầu \(\left( S \right)\):
a) Có tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\).
b) Có đường kính \(EF\) với \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\).
c) Có tâm \(M\left( { - 2;1;3} \right)\) và đi qua điểm \(N\left( {2; - 3; - 4} \right)\).
Phương pháp giải:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\) có phương trình là
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
Lời giải chi tiết:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\) có phương trình là
\({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 4} \right)^2} = 100\).
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\).
Ta có \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\), suy ra \(I\left( {5; - 2;4} \right)\).
Ta có \(EF = \sqrt {{{\left( {3 - 7} \right)}^2} + {{\left( { - 1 + 3} \right)}^2} + {{\left( {8 - 0} \right)}^2}} = 2\sqrt {21} \), suy ra \(R = \frac{{EF}}{2} = \sqrt {21} \).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 4} \right)^2} = 21\).
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\).
Ta có \(MN = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {1 + 3} \right)}^2} + {{\left( {3 + 4} \right)}^2}} = 9\).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = 81\).
VD1
Trả lời câu hỏi Vận dụng 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\) (đơn vị của các trục toạ độ là mét), các nhà nghiên cứu khí tượng dùng một phần mềm mô phỏng bề mặt của một quả bóng thám không có dạng hình cầu bằng phương trình \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\). Tìm toạ độ tâm, bán kính của quả bóng và tính khoảng cách từ tâm của quả bóng đến mặt đất có phương trình \(z = 0\).

Phương pháp giải:
Từ phương trình mặt cầu, chỉ ra tâm và bán kính của quả bóng thám không. Sau đó sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng để tính khoảng cách từ tâm của quả bóng đến mặt đất.
Lời giải chi tiết:
Phương trình bề mặt của quả bóng thám không là \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\), suy ra quả bóng có tâm \(I\left( {300;400;2000} \right)\) và bán kính \(R = 1.\)
Khoảng cách từ tâm quả bóng đến mặt đất là
\(d = \frac{{\left| {0.300 + 0.400 + 1.2000 + 0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 2000\) (mét).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 63 SGK Toán 12 Chân trời sáng tạo
a) Trong không gian \(Oxyz\), cho điểm \(M\left( {x;y;z} \right)\) thay đổi có toạ độ luôn thoả mãn phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\). (*)
i) Biến đổi (*) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\).
ii) Chứng tỏ \(M\left( {x;y;z} \right)\) luôn thuộc một mặt cầu \(\left( S \right)\). Tìm tâm và bán kính của \(\left( S \right)\).
b) Bằng cách biến đổi phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\) (**) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\), hãy cho biết phương trình (**) có thể là phương trình mặt cầu hay không.
Phương pháp giải:
a) Sử dụng các hằng đẳng thức để đưa phương trình (*) về dạng như đề bài yêu cầu, từ đó suy ra điểm \(M\) luôn thuộc mặt cầu \(\left( S \right)\).
b) Sử dụng hằng đẳng thức để đưa phương trình (**) về dạng như đề bài yêu cầu, rồi kết luận.
Lời giải chi tiết:
a)
i) Ta có
\({x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\)
\(\Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) - 25 = 0\)
\(\Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\).
ii) Do điểm \(M\left( {x;y;z} \right)\) có toạ độ thoả mãn phương trình (*), suy ra điểm \(M\) thoả mãn phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\). Vậy điểm \(M\) thuộc mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = \sqrt {25} = 5\).
b) Ta có:
\({x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\)
\(\Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) + 1 = 0\)
\(\Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\).
Do \( - 1 < 0\), nên phương trình trên không là phương trình mặt cầu. Suy ra (**) không là phương trình mặt cầu.
TH2
Trả lời câu hỏi Thực hành 2 trang 63 SGK Toán 12 Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\);
b) \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\).
Phương pháp giải:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\). Xác định \(a\), \(b\), \(c\), \(d\) và tính \({a^2} + {b^2} + {c^2} - d\), rồi rút ra kết luận.
Lời giải chi tiết:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\).
a) Với phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\), ta có \(a = 0\), \(b = 0\), \(c = - 2\) và \(d = - 32\).
Ta có \({a^2} + {b^2} + {c^2} - d = {0^2} + {0^2} + {\left( { - 2} \right)^2} + 32 = 36 > 0\).
Vậy phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\) là phương trình mặt cầu tâm \(I\left( {0;0; - 2} \right)\) và bán kính \(R = 6\).
b) Với phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\), ta có \(a = - 1\), \(b = - 1\), \(c = 1\) và \(d = 4\).
Ta có \({a^2} + {b^2} + {c^2} - d \)
\(= {\left( { - 1} \right)^2} + {\left( { - 1} \right)^2} + {1^2} - 4 = - 1 < 0\).
Vậy phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\) không là phương trình mặt cầu.
- Giải mục 2 trang 63, 64 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 1 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 2 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 3 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 4 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận