Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo

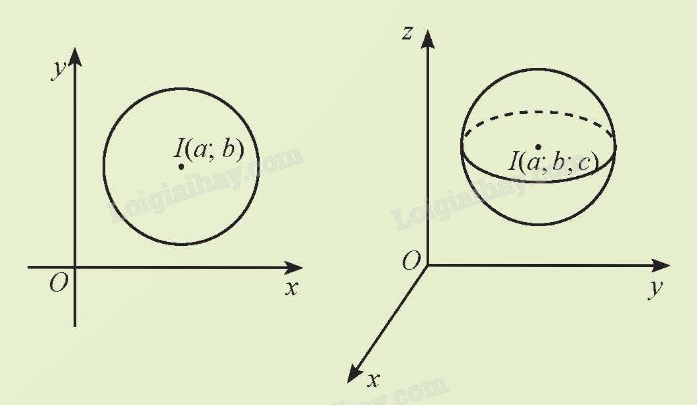
Ta đã biết trong mặt phẳng tọa độ Oxy, phương trình đường tròn tâm I(a;b), bán kính R có dạng:

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Ta đã biết trong mặt phẳng tọa độ Oxy, phương trình đường tròn tâm I(a;b), bán kính R có dạng:

\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\).

Trong không gian Oxyz, phương trình mặt cầu có dạng như thế nào?

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức đã học.

Quảng cáo

Lời giải chi tiết

Trong không gian Oxyz, mặt cầu (S) tâm I(a;b;c), bán kính R có phương trình là:

\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 - Chân trời sáng tạo
Trong không gian (Oxyz), cho mặt cầu (Sleft( {I;R} right)) có tâm (Ileft( {a;b;c} right)) và bán kính (R). Xét một điểm (Mleft( {x;y;z} right)) thay đổi. a) Tính khoảng cách (IM) theo (x), (y), (z) và (a), (b), (c). b) Nêu điều kiện cần và đủ của (x), (y), (z) để điểm (Mleft( {x;y;z} right)) nằm trên mặt cầu (Sleft( {I;R} right)).
Giải mục 2 trang 63, 64 SGK Toán 12 tập 2 - Chân trời sáng tạo
Bề mặt của một bóng thám không dạng hình cầu có phương trình ({x^2} + {y^2} + {z^2} - 200x - 600y - {rm{4 000}}z + {rm{4 099 900}} = 0). Tìm toạ độ tâm và bán kính mặt cầu.
Giải bài tập 1 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Viết phương trình mặt cầu (left( S right)): a) Có tâm (Ileft( {7; - 3;0} right)), bán kính (R = 8). b) Có tâm (Mleft( {3;1; - 4} right)) và đi qua điểm (Nleft( {1;0;1} right)). c) Có đường kính (AB) với (Aleft( {4;6;8} right)) và (Bleft( {2;4;4} right)).
Giải bài tập 2 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó. a) ({x^2} + {y^2} + {z^2} + 5x - 7y + z - 1 = 0). b) ({x^2} + {y^2} + {z^2} + 4x + 6y - 2z + 100 = 0). c) ({x^2} + {y^2} + {z^2} - x - y - z + frac{1}{2} = 0).
Giải bài tập 3 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Cho hai điểm (Aleft( {1;0;0} right)) và (Bleft( {5;0;0} right)). Chứng minh rằng nếu điểm (Mleft( {x;y;z} right)) thoả mãn (overrightarrow {MA} .overrightarrow {MB} = 0) thì (M) thuộc một mặt cầu (left( S right)). Tìm tâm và bán kính của (left( S right)).
Giải bài tập 4 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Phần mềm mô phỏng thiết bị thám hiẻm đại dương có dạng hình cầu trong không gian (Oxyz). Cho biết toạ độ tâm mặt cầu là (Ileft( {360;200;400} right)) và bán kính (r = 2{rm{ m}}). Viết phương trình mặt cầu.
Giải bài tập 5 trang 65 SGK Toán 12 tập 2 - Chân trời sáng tạo
Người ta muốn thiết kế một bồn chứa khí hoá lỏng hình cầu bằng phần mềm 3D. Cho biết phương trình bề mặt của bồn chứa là (left( S right):{left( {x - 6} right)^2} + {left( {y - 6} right)^2} + {left( {z - 6} right)^2} = 25). Phương trình mặt phẳng chứa nắp là (left( P right):z = 10). a) Tìm tâm và bán kính của bồn chứa. b) Tính khoảng cách từ tâm bồn chứa đến mặt phẳng của nắp.
Lý thuyết Phương trình mặt cầu Toán 12 Chân trời sáng tạo
1. Phương trình mặt cầu trong không gian Khái niệm mặt cầu Trong không gian, cho điểm I và số dương R. Mặt cầu tâm I, bán kính R, kí hiệu S(I;R) là tập hợp các điểm M trong không gian thỏa mãn IM = R. Đoạn thẳng nối hai điểm thuộc mặt cầu và đi qua tâm I là đường kính mặt cầu.