 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài 1. Vectơ và các phép toán trong không gian - Toán 1..
Bài 1. Vectơ và các phép toán trong không gian - Toán 1..
Giải bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và cùng có cường độ là 5N. Tính cường độ của hợp lực.
Đề bài
Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và cùng có cường độ là 5N. Tính cường độ của hợp lực.
Phương pháp giải - Xem chi tiết
Áp dụng quy tắc hình hộp.
Lời giải chi tiết
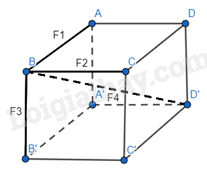
Vecto hợp lực là: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {{F_4}} \).
Cường độ của hợp lực là: \({F_4} = \sqrt {{F_{12}}^2 + F_3^2} = \sqrt {{({F_1}^2 + F_2^2)} + F_3^2} \)
\(= \sqrt {{5^2} + {5^2} + {5^2}} = 5\sqrt 3 \) N.
- Giải bài tập 4 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 5 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 6 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 7 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận