Giải bài 17 trang 65 sách bài tập toán 8 – Cánh diều

Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân \(ABC\) (\(AB = AC = 2\) m) cùng các thanh sắt nằm ngang \(GF,HE < ID,BC\) và sau đó gắn cây thông như Hình 22.

Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Cánh diều

Toán - Văn - Anh - Khoa học tự nhiên

Đề bài

Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân \(ABC\)

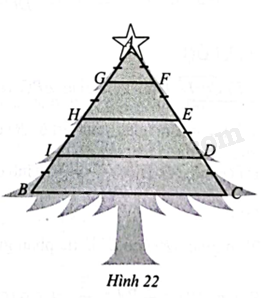
(\(AB = AC = 2\) m) cùng các thanh sắt nằm ngang \(GF,HE < ID,BC\) và sau đó gắn cây thông như Hình 22. Tính số tiền sắt cần sử dụng để làm cây thông noel đó.

Biết giác một mét sắt là 55 000 đồng và \(AG = GH = HI = IB,CD = DE = EF = FA\), thanh \(GF\) dài \(0,2\) m.

Phương pháp giải - Xem chi tiết

Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh tam giác đó.

Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.

Định lí Thales đảo: nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Lời giải chi tiết

Vì \(GF\) là đường trung bình của tam giác \(AHE\) nên \(HE = 2GF = 2.0,2 = 0,4\) (m).

Vì \(HE\) là đường trung bình của tam giác \(ABC\) nên \(BC = 2HE = 2.0,4 = 0,8\) (m).

Ta có \(\frac{{AI}}{{AB}} = \frac{{AD}}{{AC}} = \frac{3}{4}\) nên theo định lí Thales đảo \(ID//BC\) từ đó: \(\frac{{ID}}{{BC}} = \frac{{AI}}{{AB}} = \frac{3}{4}\).

Suy ra \(ID = \frac{3}{4}BC = \frac{3}{4}.0,8 = 0,6\) (m). Số tiền cần trả để hoàn thành cây thông noel đó là: \(\left( {0,2 + 0,4 + 0,6 + 0,8 + 2 + 2} \right).55000 = 330000\) (đồng).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 18 trang 66 sách bài tập toán 8 – Cánh diều
Cho hình chữ nhật \(ABCD\). Kẻ \(CH\) vuông góc với \(BD\left( {H \in BD} \right)\). Gọi \(I,K,M\) lần lượt là trung điểm của \(BH,CH,AD\). Chứng minh:
Giải bài 19 trang 66 sách bài tập toán 8 – Cánh diều
Cho tứ giác \(ABCD\) có \(AD = BC\). Đường thẳng đi qua trung điểm \(M\) và \(N\) lần lượt của các cạnh \(AB\) và \(CD\) cắt các đường thẳng \(AD\) và \(BC\) lần lượt tại \(E\) và \(F\). Chứng minh: \(\widehat {AEM} = \widehat {MFB}\).
Giải bài 20 trang 66 sách bài tập toán 8 – Cánh diều
Cho tứ giác \(ABCD\) có \(M,N\) lần lượt là trung điểm của \(AD,BC\). Chứng minh: \(MN \le \frac{{AB + DC}}{2}\). Dấu đẳng thức xảy ra khi nào?
Giải bài 16 trang 65 sách bài tập toán 8 – Cánh diều
Cho tam giác \(ABC\) cân tại \(A\), có \(M\) là trung điểm của \(BC\). Kể tia \(Mx\) song song với \(AC\) cắt \(AB\) tại \(E\) và tia \(My\) song song với \(AB\) cắt \(AC\) tại \(F\). Chứng minh:
Giải bài 15 trang 65 sách bài tập toán 8 – Cánh diều
Hình 21 cho biết cạnh của tam giác đều \(ABC\) bằng 6 cm; \(M,N\) lần lượt là trung điểm các cạnh \(AB,AC\). Chỉ ra phát biểu sai trong các phát biểu sau:
Giải bài 14 trang 65 sách bài tập toán 8 – Cánh diều
Chọn phát biểu đúng trong các phát biểu sau: a) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng một phần ba cạnh đó.