-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
-
Chương VI. Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập và phân loại dữ liệu
- Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Bài 3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ
- Bài 4. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài 5. Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản
- Bài tập cuối chương VI
-
Chương VII. Phương trình bậc nhất một ẩn
-
Chương VIII. Tam giác đồng dạng. Hình đồng dạng
- Bài 1. Định lí Thalès trong tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 9. Hình đồng dạng
- Bài tập cuối chương VIII
-
Giải bài 69 trang 85 sách bài tập toán 8 – Cánh diều
Cho tam giác \(ABC\) cân tại \(A,AB=10\)cm, \(BC=12\)cm. Gọi \(I\) là giao điểm của các đường phân giác của tam giác \(ABC\). Tính độ dài \(AI\).
Tổng hợp đề thi giữa kì 1 lớp 8 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho tam giác \(ABC\) cân tại \(A,AB=10\)cm, \(BC=12\)cm. Gọi \(I\) là giao điểm của các đường phân giác của tam giác \(ABC\). Tính độ dài \(AI\).
Phương pháp giải - Xem chi tiết
Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu:
\(\widehat{A'}=\widehat{A},\widehat{B'}=\widehat{B},\widehat{C'}=\widehat{C}\) ; \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}\).
Kí hiệu là \(\Delta A'B'C'\backsim \Delta ABC\).
Tỉ số các cạnh tương ứng \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=k\) gọi là tỉ số đồng dạng.
Lời giải chi tiết
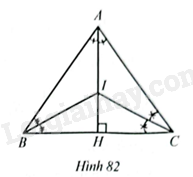
Gọi \(H\) là giao điểm của hai đường thẳng \(AI\) và \(BC\). Do tam giác \(ABC\) cân tại \(A\) nên đường phân giác \(AI\) cũng là đường cao, đường trung tuyến. Do đó \(BH=\frac{BC}{2}=6\)cm. Tam giác \(AHB\) vuông tại \(H\) nên \(A{{H}^{2}}=A{{B}^{2}}-B{{H}^{2}}={{10}^{2}}-{{6}^{2}}=64\), suy ra \(AH=8\)cm. Ta có \(\frac{AI}{IH}=\frac{AB}{BH}\) suy ra \(\frac{AI}{AI+IH}=\frac{AB}{AB+BH}\) hay \(\frac{AI}{8}=\frac{10}{10+6}=\frac{5}{8}\). Vậy \(AI=5\)cm.
Bình luận
Chia sẻ
- Giải bài 70 trang 85 sách bài tập toán 8 – Cánh diều
- Giải bài 71 trang 85 sách bài tập toán 8 – Cánh diều
- Giải bài 72 trang 85 sách bài tập toán 8 – Cánh diều
- Giải bài 73 trang 85 sách bài tập toán 8 – Cánh diều
- Giải bài 68 trang 85 sách bài tập toán 8 – Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho Lớp 8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
