Đề thi vào lớp 6 môn Toán trường THCS Nguyễn Huệ - Cẩm Giàng năm 2025

Đề bài

B. MÔN TOÁN (10 điểm)

I. PHẦN TRẮC NGHIỆM (6,0 điểm)

Ghi vào tờ giấy kiểm tra chữ cái đứng trước đáp án đúng (không làm trực tiếp vào đề)

Câu 1 (0,5 điểm): Hỗn số $8\frac{2}{5}$ viết dưới dạng số thập phân là:

A. 8,2                                      B. 8,25                                    C. 8,4

Câu 2 (0,5 điểm): 3 giờ 45 phút = ……… giờ:

A. 3,45                                    B. 3,75                                    C. $3\frac{4}{5}$

Câu 3 (0,5 điểm): Một bạn học sinh gieo một con xúc xắc 10 lần liên tiếp và ghi lại kết quả số chấm xuất hiện trong mỗi lần gieo như sau:

Hỏi tỉ số giữa số lần xuất hiện mặt có số chấm là 5 và tổng số lần đã gieo xúc xắc là bao nhiêu?

A. $\frac{1}{5}$                                             B. $\frac{1}{2}$                                              C. $\frac{3}{{10}}$

Câu 4 (0,5 điểm): Số tự nhiên thích hợp điền vào chỗ trống để có kết quả đúng là:

$\frac{8}{{21}} < \frac{{......}}{7} < \frac{9}{{20}}$

A. 3                                         B. 8                                         C. 9

Câu 5 (0,5 điểm): Trung bình cộng của hai số là 12,5. Số lớn hơn số bé là 4,2 thì số lớn là:

A. 8,35                                    B. 14,6                                    C. 10,7

Câu 6 (0,5 điểm): Một thùng hàng đựng đầy hàng có khối lượng là 180kg. Một thùng tương tự nhưng đựng một nửa lượng hàng thì có khối lượng là 105kg. Hỏi vỏ thùng hàng có khối lượng là bao nhiêu ki-lô-gam?

A. 30                                       B. 75                                       C. 37,5

Câu 7 (0,5 điểm): Nếu ta tăng số lớn lên 4 lần và tăng số bé 2 lần thì thương của số lớn và số bé thay đổi như thế nào?

A. Giảm 2 lần                          B. Tăng 2 lần                          C. Tăng 8 lần

Câu 8 (0,5 điểm): Số học sinh dự tuyển vào lớp 6 trường THCS A năm học 2024 - 2025 là 500 học sinh. Năm

học 2025 – 2026 só học sinh dự tuyển giảm 6% so với năm học 2024 - 2025. Hỏi năm học 2025 – 2026 trường THCS A có bao nhiêu học sinh dự tuyển vào lớp 6?

A. 470                                     B. 494                                     C. 530

Câu 9 (0,5 điểm): Người gác đường đứng nhìn đoàn tàu đi qua trước mặt mình hết 15 giây với vận tốc 36km/giờ. Hỏi tàu dài bao nhiêu mét?

A. 540                                     B. 150                                     C. 360

Câu 10 (0,5 điểm): Bể cá dạng hình hộp chữ nhật dài 1,5m, rộng 1m và cao 1,2m. Bể đang chứa 1200 lít nước. Để nước đầy bể, cần bơm thêm bao nhiêu lít nước?

A. 1200                                   B. 300                                     C. 600

Câu 11 (0,5 điểm): Cho hình thang ABCD có tổng hai đáy bằng 80 cm và diện tích bằng 320 cm² thì chiều cao của hình thang là

A. 4 cm                                   B. 8 cm                                    C. 2 cm

Câu 12 (0,5 điểm): Nam và Bình là hai chị em sinh đôi và họ có một anh trai. Tổng số tuổi của ba anh em là 42 tuổi. Tìm tuổi của Nam biết tuổi của anh trai bằng $\frac{3}{2}$ tuổi của Nam.

A. 12                                       B. 13                                       C. 14

II. PHẦN TỰ LUẬN (4,0 điểm)

Câu 1 (1,5 điểm)

a) Tính:           $25\%  \times 132\frac{3}{5} + 132,6 \times \frac{3}{4}$

b) Tìm quy luật và tìm số thứ 2025 của dãy số sau: 1 ; 4 ; 7 ; 10 ; ….

Câu 2 (2,0 điểm)

Cho hình chữ nhật ABCD có chu vi là 160 cm, chiều dài AB hơn chiều rộng BC là 40 cm.

a) Tính diện tích hình chữ nhật ABCD.

b) Trên DC lấy điểm I sao cho DI = 20 cm. Người ta mở rộng hình chữ nhật bằng cách kéo dài BC về phía C cắt AI tại K (như hình 1). Tính tỉ số của KI và AI.

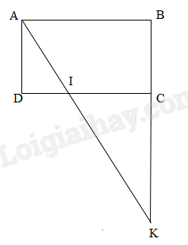
Đáp án

Câu 1 (0,5 điểm): Hỗn số $8\frac{2}{5}$ viết dưới dạng số thập phân là:

A. 8,2                                      B. 8,25                                    C. 8,4

Cách giải

$8\frac{2}{5} = 8 + 0,4 = 8,4$

Đáp án: C

Câu 2 (0,5 điểm): 3 giờ 45 phút = ……… giờ:

A. 3,45                                    B. 3,75                                    C. $3\frac{4}{5}$

Cách giải

3 giờ 45 phút = 3 giờ + 0,75 giờ = 3,75 giờ

Đáp án: B

Câu 3 (0,5 điểm): Một bạn học sinh gieo một con xúc xắc 10 lần liên tiếp và ghi lại kết quả số chấm xuất hiện trong mỗi lần gieo như sau:

Hỏi tỉ số giữa số lần xuất hiện mặt có số chấm là 5 và tổng số lần đã gieo xúc xắc là bao nhiêu?

A. $\frac{1}{5}$                                             B. $\frac{1}{2}$                                              C. $\frac{3}{{10}}$

Cách giải:

Tỉ số giữa số lần xuất hiện mặt có số chấm là 5 và tổng số lần đã gieo xúc xắc là $\frac{2}{{10}} = \frac{1}{5}$

Đáp án: A

Câu 4 (0,5 điểm): Số tự nhiên thích hợp điền vào chỗ trống để có kết quả đúng là:

$\frac{8}{{21}} < \frac{{......}}{7} < \frac{9}{{20}}$

A. 3                                         B. 8                                         C. 9

Cách giải

Ta có $\frac{8}{{21}} < \frac{3}{7} < \frac{9}{{20}}$

Đáp án: A

Câu 5 (0,5 điểm): Trung bình cộng của hai số là 12,5. Số lớn hơn số bé là 4,2 thì số lớn là:

A. 8,35                                    B. 14,6                                    C. 10,7

Cách giải:

Tổng hai số là: 12,5 x 2 = 25

Số lớn là (25 + 4,2) : 2 = 14,6

Đáp án: B

Câu 6 (0,5 điểm): Một thùng hàng đựng đầy hàng có khối lượng là 180kg. Một thùng tương tự nhưng đựng một nửa lượng hàng thì có khối lượng là 105kg. Hỏi vỏ thùng hàng có khối lượng là bao nhiêu ki-lô-gam?

A. 30                                       B. 75                                       C. 37,5

Cách giải

Một nửa khối lượng hàng hoá trong thùng là 180 – 105 = 75 (kg)

Khối lượng hàng hoá khi đựng đầy thùng là 75 x 2 = 150 (kg)

Vỏ thùng hàng có khối lượng là: 180 – 150 = 30 (kg)

Đáp án: A

Câu 7 (0,5 điểm): Nếu ta tăng số lớn lên 4 lần và tăng số bé 2 lần thì thương của số lớn và số bé thay đổi như thế nào?

A. Giảm 2 lần                          B. Tăng 2 lần                          C. Tăng 8 lần

Cách giải:

Ta tăng số lớn lên 4 lần và tăng số bé 2 lần tương đương với tăng số lớn lên 2 lần và giữ nguyên số bé.

Vậy thương tăng lên 2 lần.

Đáp án: B

Câu 8 (0,5 điểm): Số học sinh dự tuyển vào lớp 6 trường THCS A năm học 2024 - 2025 là 500 học sinh. Năm

học 2025 – 2026 số học sinh dự tuyển giảm 6% so với năm học 2024 - 2025. Hỏi năm học 2025 – 2026 trường THCS A có bao nhiêu học sinh dự tuyển vào lớp 6?

A. 470                                     B. 494                                     C. 530

Cách giải:

Năm học 2025 – 2026 số học sinh dự tuyển giảm 6% so với năm học 2024 – 2025.

Nên số học sinh dự tuyển năm học 2025 – 2026 chiếm 94% so với năm học 2024 – 2025.

Năm học 2025 – 2026 trường THCS A có số học sinh dự tuyển vào lớp 6 là:

500 x 94 : 100 = 470 (học sinh)

Đáp án: A

Câu 9 (0,5 điểm): Người gác đường đứng nhìn đoàn tàu đi qua trước mặt mình hết 15 giây với vận tốc 36km/giờ. Hỏi tàu dài bao nhiêu mét?

A. 540                                     B. 150                                     C. 360

Cách giải:

Đoàn tàu dài là: 36 x 15 = 540 (m)

Đáp án: A

Câu 10 (0,5 điểm): Bể cá dạng hình hộp chữ nhật dài 1,5m, rộng 1m và cao 1,2m. Bể đang chứa 1200 lít nước. Để nước đầy bể, cần bơm thêm bao nhiêu lít nước?

A. 1200                                   B. 300                                     C. 600

Cách giải

Thể tích bể cá là 1,5 x 1 x 1,2 = 1,8 (m³) = 1 800 dm³ = 1 800 lít

Để nước đầy bể, cần bơm thêm số lít nước là: 1 800 – 1 200 = 600 (lít)

Đáp án: C

Câu 11 (0,5 điểm): Cho hình thang ABCD có tổng hai đáy bằng 80 cm và diện tích bằng 320 cm² thì chiều cao của hình thang là

A. 4 cm                                   B. 8 cm                                    C. 2 cm

Cách giải

Chiều cao của hình thang ABCD là: 320 x 2 : 80 = 8 (cm)

Đáp án: B

Câu 12 (0,5 điểm): Nam và Bình là hai chị em sinh đôi và họ có một anh trai. Tổng số tuổi của ba anh em là 42 tuổi. Tìm tuổi của Nam biết tuổi của anh trai bằng $\frac{3}{2}$ tuổi của Nam.

A. 12                                       B. 13                                       C. 14

Cách giải

Coi tuổi của anh trai là 3 phần, tuổi Nam là 2 phần, tuổi của Bình là 2 phần.

Tổng số phần bằng nhau là: 3 + 2 + 2 = 7 (phần)

Tuổi của Nam là 42 : 7 x 2 = 12 (tuổi)

Đáp án: A

II. PHẦN TỰ LUẬN (4,0 điểm)

Câu 1 (1,5 điểm)

a) Tính:           $25\%  \times 132\frac{3}{5} + 132,6 \times \frac{3}{4}$

b) Tìm quy luật và tìm số thứ 2025 của dãy số sau: 1 ; 4 ; 7 ; 10 ; ….

Cách giải:

a) $25\%  \times 132\frac{3}{5} + 132,6 \times \frac{3}{4}$

$ = 0,25 \times 132,6 + 132,6 \times 0,75$

$ = 132,6 \times (0,25 + 0,75)$

$ = 132,6$

b) Tìm quy luật và tìm số thứ 2025 của dãy số sau: 1 ; 4 ; 7 ; 10 ; ….

Cách giải:

Số thứ hai: 4 = 3 x 1 + 1

Số thứ ba: 7 = 3 x 2 + 1

Số thứ tư: 10 = 3 x 3 + 1

........

Số thứ n = 3 x (n – 1) + 1

Vậy số thứ 2025 là 3 x 2024 + 1 = 6073.

Câu 2 (2,0 điểm)

Cho hình chữ nhật ABCD có chu vi là 160 cm, chiều dài AB hơn chiều rộng BC là 40 cm.

a) Tính diện tích hình chữ nhật ABCD.

b) Trên DC lấy điểm I sao cho DI = 20 cm. Người ta mở rộng hình chữ nhật bằng cách kéo dài BC về phía C cắt AI tại K (như hình 1). Tính tỉ số của KI và AI.

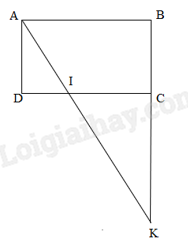
a) Nửa chu vi hình chữ nhật ABCD là: 160 : 2 = 80 (cm)

Chiều dài AB là (80 + 40) : 2 = 60 (cm)

Chiều rộng hình chữ nhật là: 80 – 60 = 20 (cm)

Diện tích hình chữ nhật ABCD là: 60 x 20 = 1 200 (cm²)

b) Nối D với K

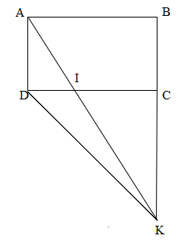
Ta có $\frac{{DI}}{{DC}} = \frac{{20}}{{60}} = \frac{1}{3}$

S_ADI = $\frac{1}{3}$S_ADK (Chung đáy AD và chiều cao hạ từ I xuống AD = $\frac{1}{3}$chiều cao hạ từ K xuống AD)

Suy ra S_ADI = $\frac{1}{2}$S_DIK

Suy ra AI = $\frac{1}{2}$IK (Hai tam giác có chung đáy IK và S_ADI = $\frac{1}{2}$S_DIK)