Đề thi vào lớp 6 môn Toán thành phố Thủ Đức năm 2025

Đề bài

Bài 1. (3,0 điểm) Điền số thích hợp vào chỗ trống.

Một bản báo cáo về khối lượng trái cây bán được trong tháng 4 của cửa hàng A bị rách một phần, những thông tin còn lại được thể hiện như hình 1:

Biết doanh thu trong tháng 4 năm 2025 của 3 loại trái cây: 8 250 000 đồng. Vậy:

- Số tiền bán sầu riêng trong tháng 4 năm 2025 là:                                                             đồng.

- Số tiền bán xoài trong tháng 4 năm 2025 là:                                                                     đồng.

- Khối lượng chuối bán được trong tháng 4 năm 2025 là:                                                  kg.

Bài 2. (3,0 điểm) Điền số thích hợp vào chỗ trống.

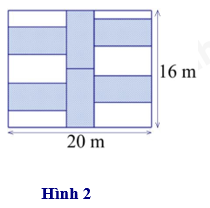
Một khu vườn hình chữ nhật có chiều dài là 20 m, chiều rộng là 16 m. Bác Nguyên dự tính xây dựng 6 khu vực trồng rau có dạng hình chữ nhật với các kích thước bằng nhau (phần in đậm) như hình 2. Vậy:

- Chu vi của một khu vực trồng rau là:      m.

- Chu vi khu vực trồng rau (phần in đậm) là:                                        m.

Bài 3. (3,0 điểm) Điền số thích hợp vào chỗ trống.

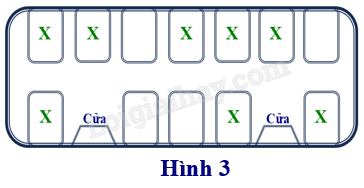
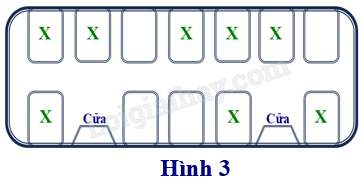
Bạn Thành và bạn Tiên cùng lên một toa tàu điện. Sơ đồ chỗ ngồi trên toa tàu được bố trí như hình 3. Trong đó, những vị trí X đã có người ngồi và hai bạn thấy chỉ còn 4 chỗ trống. Vậy:

- Số cách sắp xếp chỗ ngồi của bạn Thành và bạn Tiên trên toa tàu là:            cách.

Tỉ số giữa số cách sắp xếp chỗ ngồi mà bạn Thành và bạn Tiên có thể ngồi cạnh nhau so với tất cả các cách sắp xếp chỗ ngồi của hai bạn này là:            .

Bài 4. (6,0 điểm) Có hai thùng đựng nước dạng hình hộp chữ nhật. Thùng A có chiều dài 50 cm, chiều rộng 30 cm và chiều cao 70 cm. Thùng B có chiều dài 60 cm, chiều rộng 50 cm và chiều cao 55 cm.

a/ Tính thể tích mỗi thùng theo đơn vị lít.

b/ Biết thùng A đang chứa đầy nước và thùng B không chứa nước. Người ta đổ nước từ thùng A qua thùng B sao cho chiều cao mực nước trong thùng A gấp đôi chiều cao mực nước trong thùng B. Tính chiều cao mực nước trong thùng B lúc sau (biết lượng nước đổ ra ngoài không đáng kể).

Thí sinh trình bày đầy đủ các bước giải của Bài 4 vào chỗ trống.

Đáp án

Bài 1. (3,0 điểm) Điền số thích hợp vào chỗ trống.

Một bản báo cáo về khối lượng trái cây bán được trong tháng 4 của cửa hàng A bị rách một phần, những thông tin còn lại được thể hiện như hình 1:

Biết doanh thu trong tháng 4 năm 2025 của 3 loại trái cây: 8 250 000 đồng. Vậy:

- Số tiền bán sầu riêng trong tháng 4 năm 2025 là: 80 000 x 40 = 3 200 000 đồng.

- Số tiền bán xoài trong tháng 4 năm 2025 là: 65 000 x 50 = 3 250 000 đồng.

Số tiền bán chuối trong tháng 4 năm 2025 là:

8 250 000 – (3 200 000 + 3 250 000) = 1 800 000 đồng

- Khối lượng chuối bán được trong tháng 4 năm 2025 là: 1 800 000 : 40 = 45 kg.

Bài 2. (3,0 điểm) Điền số thích hợp vào chỗ trống.

Một khu vườn hình chữ nhật có chiều dài là 20 m, chiều rộng là 16 m. Bác Nguyên dự tính xây dựng 6 khu vực trồng rau có dạng hình chữ nhật với các kích thước bằng nhau (phần in đậm) như hình 2. Vậy:

- Chu vi của một khu vực trồng rau là: 24 m. (mỗi khu vực trồng rau có chiều dài 16 : 2 = 8 m, chiều rộng là 20 : 5 = 4 m)

- Chu vi khu vực trồng rau (phần in đậm) là: 8 x 8 + 4 x 10 = 104 m.

Bài 3. (3,0 điểm) Điền số thích hợp vào chỗ trống.

Bạn Thành và bạn Tiên cùng lên một toa tàu điện. Sơ đồ chỗ ngồi trên toa tàu được bố trí như hình 3. Trong đó, những vị trí X đã có người ngồi và hai bạn thấy chỉ còn 4 chỗ trống. Vậy:

- Số cách sắp xếp chỗ ngồi của bạn Thành và bạn Tiên trên toa tàu là: 4 x 3 = 12 cách.

Tỉ số giữa số cách sắp xếp chỗ ngồi mà bạn Thành và bạn Tiên có thể ngồi cạnh nhau so với tất cả các cách sắp xếp chỗ ngồi của hai bạn này là: $\frac{2}{{12}} = \frac{1}{6}$.

Bài 4. (6,0 điểm) Có hai thùng đựng nước dạng hình hộp chữ nhật. Thùng A có chiều dài 50 cm, chiều rộng 30 cm và chiều cao 70 cm. Thùng B có chiều dài 60 cm, chiều rộng 50 cm và chiều cao 55 cm.

a/ Tính thể tích mỗi thùng theo đơn vị lít.

b/ Biết thùng A đang chứa đầy nước và thùng B không chứa nước. Người ta đổ nước từ thùng A qua thùng B sao cho chiều cao mực nước trong thùng A gấp đôi chiều cao mực nước trong thùng B. Tính chiều cao mực nước trong thùng B lúc sau (biết lượng nước đổ ra ngoài không đáng kể).

Bài giải

a)

Thể tích của thùng A là:

30 × 50 × 70 = 105 000 (cm³)

Đổi: 105 000 cm³ = 105 dm³ = 105 lít

Thể tích của thùng B là:

60 × 50 × 55 = 165 000 (cm³)

Đổi: 165 000 cm³ = 165 dm³ = 165 lít

b)

Diện tích đáy của thùng A là:

50 × 30 = 1 500 (cm²)

Diện tích đáy của thùng B là:

60 × 50 = 3 000 (cm²)

Tỉ số giữa diện tích đáy của thùng B và diện tích đáy của

thùng A là: 3000 : 1500 = 2

Vì diện tích đáy thùng B gấp đôi diện tích đáy thùng A nên để chiều cao mực nước của thùng A gấp đôi chiều cao mực nước của thùng B thì thể tích nước trong thùng A bằng thể tích nước trong thùng B.

Thể tích nước trong thùng B lúc sau là:

105 000 ∶ 2 = 52 500 (cm³)

Chiều cao mực nước trong thùng B lúc sau là:

52 500 ∶ 3 000 = 17,5 (cm)

Đáp số: a) Thùng A: 105 lít; thùng B: 165 lít. 

b) 17,5 cm