Đề thi học kì 1 Toán 8 - Đề số 5 - Kết nối tri thức
Phần trắc nghiệm (3 điểm) Câu 1: Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
Đề bài
Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
-
A.
4698.
-
B.
6400.
-
C.
4649.
-
D.
4600.
Tính giá trị của biểu thức: 302 + 452 - 252 + 60.45 được kết quả là
-
A.
50000.
-
B.
10000.
-
C.
9000.
-
D.
5000.
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
a. \(\left( {5{x^2} - 4x} \right)\left( {x - 2} \right)\)
b. \(\left( {15x{y^2} + 19x{y^3} + 16{y^2}} \right):6{y^2}\)
c. \(\left( { - 4{x^2}{y^2} + 8{x^3}y - 10xy} \right):2xy\)
1. \( - 2xy + 4{x^2} - 5\)
2. \(\frac{5}{2}x + \frac{{19}}{6}xy + \frac{8}{3}\)
3. \(5{x^3} - 14{x^2} + 8x\)
-
A.
Ba hình bình hành.
-
B.
Bốn hình bình hành.
-
C.
Năm hình bình hành.
-
D.
Sáu hình bình hành.
Tứ giác là hình chữ nhật nếu:
-
A.
Là tứ giác có hai đường chéo bằng nhau.
-
B.
Là hình thang có hai góc vuông.
-
C.
Là hình thang có một góc vuông.
-
D.
Là hình bình hành có một góc vuông.
Tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Vẽ ME, NF cùng vuông góc với BC (E, F thuộc BC). Khẳng định sai là:
-
A.
MN // EF.
-
B.
ME = NF.
-
C.
MN = ME.
-
D.
MN = EF.
Cho tam giác ABC có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi tam giác DEF là:
-
A.
40cm.
-
B.
160cm.
-
C.
80cm.
-
D.
20cm.
-
A.
6.
-
B.
4.
-
C.
2.
-
D.
1.
Cho tam giác ABC, AD là tia phân giác trong của góc A. Hãy chọn câu sai.
-
A.
\(\frac{{DC}}{{DB}} = \frac{{AC}}{{AB}}\).
-
B.
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\).
-
C.
\(\frac{{AB}}{{DB}} = \frac{{DC}}{{AC}}\).
-
D.
\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
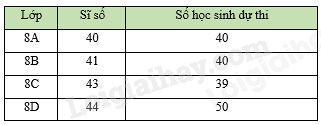
Thống kê số lượng học sinh từng lớp ở khối 8 của một trường THCS dự thi hết học kì I môn Toán. Số liệu trong bảng bên không hợp lí là:
-
A.
Số học sinh dự thi lớp 8A
-
B.
Số học sinh dự thi lớp 8B
-
C.
Số học sinh dự thi lớp 8C
-
D.
Số học sinh dự thi lớp 8D
Biểu đồ đoạn thẳng biểu diễn sô lượt người nước ngoài đến Việt Nam qua các năm 2018; 2019; 2020; 2021. (đơn vị: nghìn lượt người)
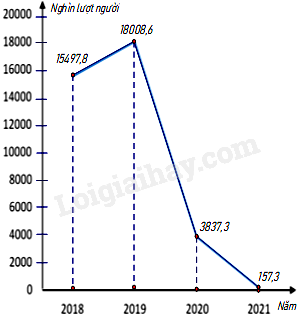
(Nguồn: Niên giám thống kê 2021)
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ đoạn thẳng ở hình bên ?
-
A.
Biểu đồ hình quạt tròn.
-
B.
Biểu đồ cột kép.
-
C.
Biểu đồ cột.
-
D.
A; B; C đều đúng.
Số lượt người nước ngoài đến Việt Nam năm 2019 là bao nhiêu nghìn lượt người ?
-
A.
15497,8.
-
B.
18008,6.
-
C.
3837,3.
-
D.
157,3.
So với năm 2018 số lượt người nước ngoài đến Việt Nam năm 2019 tăng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười) ?
-
A.
16,2%.
-
B.
18,2%.
-
C.
37,3%.
-
D.
17,3%.
Lời giải và đáp án
Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
-
A.
4698.
-
B.
6400.
-
C.
4649.
-
D.
4600.
Đáp án : D
- Rút gọn đa thức.
- Thay x = 73 và y = 26 vào đa thức để tính giá trị.
Ta có:
\(\begin{array}{l}{x^2} - {y^2} - 2y - 1\\ = {x^2} - \left( {{y^2} + 2y + 1} \right)\\ = {x^2} - {\left( {y + 1} \right)^2}\\ = \left( {x - y - 1} \right)\left( {x + y + 1} \right)\end{array}\)
Thay x = 73 và y = 26, ta được:
\(\left( {73 - 26 - 1} \right)\left( {73 + 26 + 1} \right) = 46.100 = 4600\).
Tính giá trị của biểu thức: 302 + 452 - 252 + 60.45 được kết quả là
-
A.
50000.
-
B.
10000.
-
C.
9000.
-
D.
5000.
Đáp án : D
Sử dụng hằng đẳng thức để tính nhanh biểu thức.
Ta có:
\(\begin{array}{l}{30^2} + {45^2} - {25^2} + 60.45\\ = {30^2} + {45^2} - {25^2} + 2.30.45\\ = \left( {{{30}^2} + 2.30.45 + {{45}^2}} \right) - {25^2}\\ = {\left( {30 + 45} \right)^2} - {25^2}\\ = {75^2} - {25^2}\\ = \left( {75 - 25} \right)\left( {75 + 25} \right)\\ = 50.100 = 5000\end{array}\)
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
a. \(\left( {5{x^2} - 4x} \right)\left( {x - 2} \right)\)
b. \(\left( {15x{y^2} + 19x{y^3} + 16{y^2}} \right):6{y^2}\)
c. \(\left( { - 4{x^2}{y^2} + 8{x^3}y - 10xy} \right):2xy\)
1. \( - 2xy + 4{x^2} - 5\)
2. \(\frac{5}{2}x + \frac{{19}}{6}xy + \frac{8}{3}\)
3. \(5{x^3} - 14{x^2} + 8x\)
a. \(\left( {5{x^2} - 4x} \right)\left( {x - 2} \right)\)
3. \(5{x^3} - 14{x^2} + 8x\)
b. \(\left( {15x{y^2} + 19x{y^3} + 16{y^2}} \right):6{y^2}\)
2. \(\frac{5}{2}x + \frac{{19}}{6}xy + \frac{8}{3}\)
c. \(\left( { - 4{x^2}{y^2} + 8{x^3}y - 10xy} \right):2xy\)
1. \( - 2xy + 4{x^2} - 5\)
Sử dụng các quy tắc tính đa thức.
\(\begin{array}{l}a.\,\left( {5{x^2} - 4x} \right)\left( {x - 2} \right)\\ = 5{x^3} - 4{x^2} - 10{x^2} + 8x\\ = 5{x^3} - 14{x^2} + 8x\end{array}\)
\( \Rightarrow \) a – 3.
\(\begin{array}{l}b.\,\left( {15x{y^2} + 19x{y^3} + 16{y^2}} \right):6{y^2}\\ = 15x{y^2}:6{y^2} + 19x{y^3}:6{y^2} + 16{y^2}:6{y^2}\\ = \frac{5}{2}x + \frac{{19}}{6}xy + \frac{8}{3}\end{array}\)
\( \Rightarrow \) b – 2.
\(\begin{array}{l}c.\,\left( { - 4{x^2}{y^2} + 8{x^3}y - 10xy} \right):2xy\\ = - 4{x^2}{y^2}:2xy + 8{x^3}y:2xy - 10xy:2xy\\ = - 2xy + 4{x^2} - 5\end{array}\)
\( \Rightarrow \) c – 1.
Đáp án: a – 3; b – 2; c – 1.
-
A.
Ba hình bình hành.
-
B.
Bốn hình bình hành.
-
C.
Năm hình bình hành.
-
D.
Sáu hình bình hành.
Đáp án : D
Sử dụng kiến thức về hình bình hành.
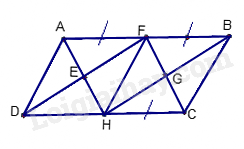
Các hình bình hành trong hình là: ABCD; AFHD; AFCH; FBCH; FBHD; EFGH. Vậy có 6 hình bình hành.
Tứ giác là hình chữ nhật nếu:
-
A.
Là tứ giác có hai đường chéo bằng nhau.
-
B.
Là hình thang có hai góc vuông.
-
C.
Là hình thang có một góc vuông.
-
D.
Là hình bình hành có một góc vuông.
Đáp án : D
Dựa vào kiến thức về hình chữ nhật.
Tứ giác có hai đường chéo bằng nhau có thể là hình thang cân nên A sai.
Hình thang có một góc vuông, hai góc vuông là hình thang vuông nên B, C sai.
Hình bình hành có một góc vuông là hình chữ nhật nên D đúng.
Tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Vẽ ME, NF cùng vuông góc với BC (E, F thuộc BC). Khẳng định sai là:
-
A.
MN // EF.
-
B.
ME = NF.
-
C.
MN = ME.
-
D.
MN = EF.
Đáp án : C
Dựa vào kiến thức về đường trung bình trong tam giác và dấu hiệu nhận biết hình học.
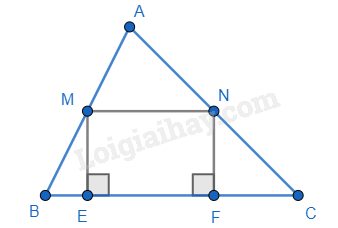
Ta có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác ABC nên MN // BC và MN = \(\frac{1}{2}\)BC. => MN // EF (E,F \( \in \) BC) nên A đúng.
Ta có ME \( \bot \) BC, NF \( \bot \) BC => ME // NF.
Tứ giác MNFE có MN // EF (E,F \( \in \) BC); ME // NF nên MNFE là hình bình hành.
=> MN = EF; ME = NF (cặp cạnh tương ứng) nên B và D đúng.
MN = ME không có đủ điều kiện để xác định nên C sai.
Cho tam giác ABC có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi tam giác DEF là:
-
A.
40cm.
-
B.
160cm.
-
C.
80cm.
-
D.
20cm.
Đáp án : A
Sử dụng tính chất của đường trung bình để tính.
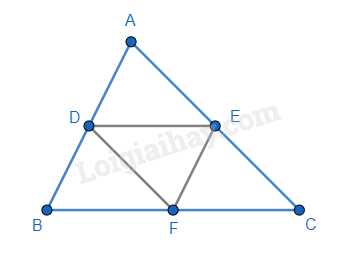
Ta có D, E, F là trung điểm của các cạnh AB, AC, BC nên DE, EF và DF là đường trung bình của tam giác ABC => \(DE = \frac{1}{2}BC;EF = \frac{1}{2}AB;DF = \frac{1}{2}AC\).
=> Chu vi tam giác DEF là: DE + EF + DF = \(\frac{1}{2}\)BC + \(\frac{1}{2}\)AB + \(\frac{1}{2}\)AC = \(\frac{1}{2}\)(BC + AB + AC) = \(\frac{1}{2}\).80 = 40(cm).
-
A.
6.
-
B.
4.
-
C.
2.
-
D.
1.
Đáp án : C
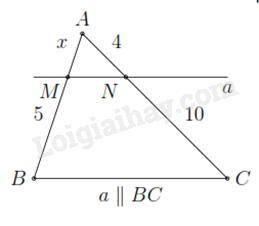
Sử dụng định lí Thales.
Do a // BC, áp dụng định lí Thales ta có:
\(\begin{array}{l}\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\\\frac{x}{5} = \frac{4}{{10}}\\x = 2\end{array}\)
Cho tam giác ABC, AD là tia phân giác trong của góc A. Hãy chọn câu sai.
-
A.
\(\frac{{DC}}{{DB}} = \frac{{AC}}{{AB}}\).
-
B.
\(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\).
-
C.
\(\frac{{AB}}{{DB}} = \frac{{DC}}{{AC}}\).
-
D.
\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\).
Đáp án : C
Sử dụng tính chất của đường phân giác trong tam giác.
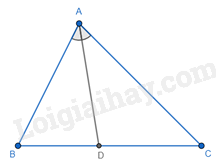
Ta có AD là tia phân giác của tam giác ABC nên:
+) \(\frac{{DC}}{{DB}} = \frac{{AC}}{{AB}}\) nên A đúng.
+) \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}\) nên B đúng.
+) \(\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}} \ne \frac{{DC}}{{AC}}\) nên C sai.
+) \(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}\) nên D đúng.
Thống kê số lượng học sinh từng lớp ở khối 8 của một trường THCS dự thi hết học kì I môn Toán. Số liệu trong bảng bên không hợp lí là:
-
A.
Số học sinh dự thi lớp 8A
-
B.
Số học sinh dự thi lớp 8B
-
C.
Số học sinh dự thi lớp 8C
-
D.
Số học sinh dự thi lớp 8D
Đáp án : D
Quan sát bảng thống kê để chỉ ra dữ liệu chưa hợp lý
Quan sát bảng thống kê, ta thấy lớp 8D có sĩ số 44 học sinh nhưng số học sinh dự thi là 50 > 44 không hợp lí.
Biểu đồ đoạn thẳng biểu diễn sô lượt người nước ngoài đến Việt Nam qua các năm 2018; 2019; 2020; 2021. (đơn vị: nghìn lượt người)
(Nguồn: Niên giám thống kê 2021)
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ đoạn thẳng ở hình bên ?
-
A.
Biểu đồ hình quạt tròn.
-
B.
Biểu đồ cột kép.
-
C.
Biểu đồ cột.
-
D.
A; B; C đều đúng.
Đáp án: C
Quan sát biểu đồ để trả lời câu hỏi.
Dữ liệu trên còn có thể biểu diễn bằng biểu đồ cột.
Số lượt người nước ngoài đến Việt Nam năm 2019 là bao nhiêu nghìn lượt người ?
-
A.
15497,8.
-
B.
18008,6.
-
C.
3837,3.
-
D.
157,3.
Đáp án: B
Quan sát biểu đồ để trả lời câu hỏi.
Số lượt người nước ngoài đến Việt Nam năm 2019 là 18008,6 nghìn lượt người.
So với năm 2018 số lượt người nước ngoài đến Việt Nam năm 2019 tăng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần mười) ?
-
A.
16,2%.
-
B.
18,2%.
-
C.
37,3%.
-
D.
17,3%.
Đáp án: A
Quan sát biểu đồ để trả lời câu hỏi.
Số lượt người nước ngoài đến Việt Nam năm 2018 là 15497,8 nghìn lượt người.
Số lượt người nước ngoài đến Việt Nam năm 2019 hơn năm 2018 là: 18008,6 - 15497,8 = 2510,8 (nghìn lượt người).
So với năm 2018 số lượt người nước ngoài đến Việt Nam năm 2019 tăng: \(\frac{{2510,8}}{{15497,8}}.100\% \approx 16,2\% \)
Sử dụng các phương pháp phân tích đa thức thành nhân tử đã học.
a) a2b + 3ab = ab(a + 3).
b) x2 \(-\) 2x + 1 = (x – 1)2.
c) x3 \(-\) 6x2 + 9x \(-\) xy2 = x(x2 – 6x + 9 – y2) = x[(x – 3)2 – y2] = x(x – 3 – y)(x – 3 + y).
a) Nhóm nhân tử chung để tìm x.
b) Biến đổi bằng hằng đẳng thức \({a^2} - 2ab + {b^2} = {\left( {a - b} \right)^2}\).
a) \({x^2} + 3x = 0\)
\(\begin{array}{l}x(x + 3) = 0\\\left[ \begin{array}{l}x = 0\\x + 3 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = - 3\end{array} \right.\end{array}\)
Vậy x = 0 hoặc x = -3.
b) Ta có: \({x^2} - 4x + 7 = {x^2} - 4x + 4 + 3 = {\left( {x - 2} \right)^2} + 3\)
Vì \({\left( {x - 2} \right)^2} \ge 0\) với mọi \(x \in \mathbb{R}\) nên \({\left( {x - 2} \right)^2} + 3 \ge 3\) với mọi \(x \in \mathbb{R}\).
Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức x2 \(-\) 4x + 7.
Vậy giá trị nhỏ nhất của x2 \(-\) 4x + 7 bằng 3 khi x – 2 = 0 hay x = 2.
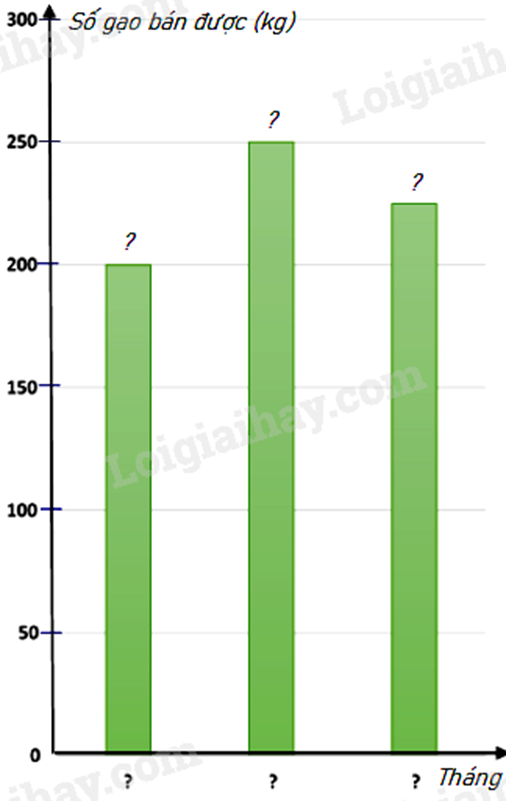
a) Dựa vào dữ liệu đề bài cho để điền vào bảng.
b) Điền số tương ứng vào biểu đồ.
a)
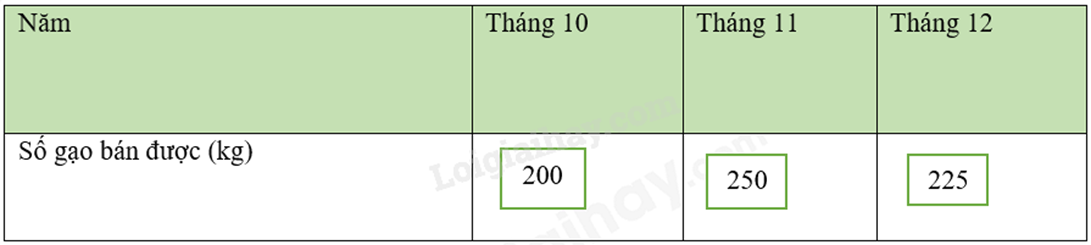
b) Biểu đồ cột biểu diễn các dữ liệu có trong biểu đồ tranh là :
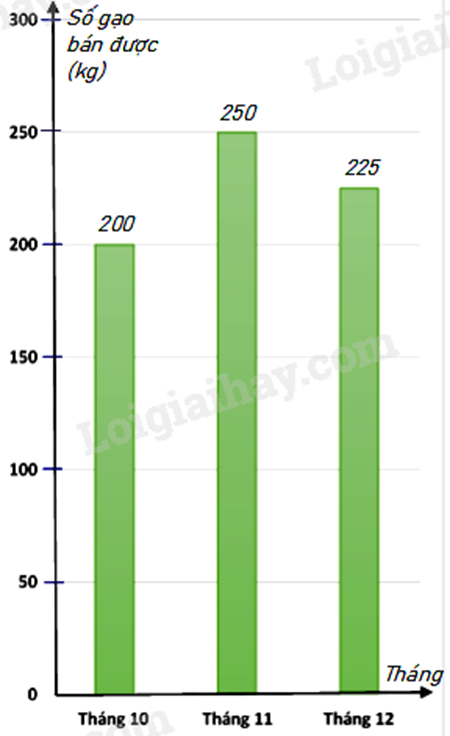
1. Dựa vào tính chất của đường trung bình để tính.
2.
a) Chứng minh BDEF có hai cạnh đối song song và bằng nhau.
b) Gọi K là giao điểm của DF và BH. Chứng minh DF \( \bot \) BH tại K và BK = KH.
c) Để BDEF là hình chữ nhật thì cần thêm điều kiện có một góc vuông.
1.
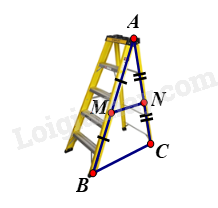
Gọi MN là thanh ngang; BC là độ rộng giữa hai bên thang.
MN nằm chính giữa thang nên M; N là trung điểm AB và AC.
Suy ra MN là đường trung bình của tam giác ABC.
Suy ra MN = \(\frac{1}{2}BC = \frac{1}{2}.80 = 40\,\,(cm)\).
Vậy người thợ đã làm thanh ngang đó dài 40 cm.
2.
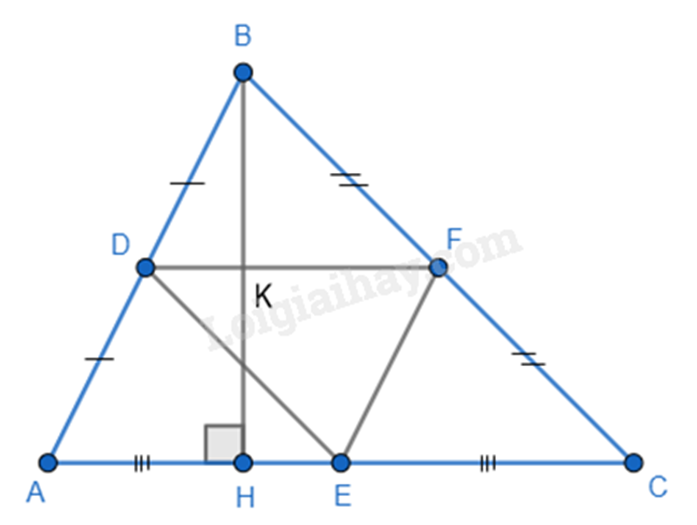
a) Ta có D, E là trung điểm của AB và AC nên DE là đường trung bình của tam giác ABC, khi đó DE // BC và DE = \(\frac{1}{2}\) (1)
Mà F là trung điểm của BC nên BF = FC = \(\frac{1}{2}\) BC. (2)
Từ (1) và (2) suy ra DE // BF (F \( \in \) BC) và DE = BF (=\(\frac{1}{2}\)BC) => BDEF là hình bình hành.
b) Tương tự, ta chứng minh được DF // AC; mà BH \( \bot \) AC nên BH \( \bot \) DF.
Gọi K là giao điểm của BH và DF.
Xét tam giác ABH có DK // AH; D là trung điểm của AB nên K là trung điểm của BH, hay BK = KH.
Do đó B và H đối xứng với nhau qua DF.
c) BDEF là hình chữ nhật khi và chỉ khi \(\widehat B = {90^0}\). Khi đó tam giác ABC vuông tại B.
Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức.
Ta có: \(A = {({n^2} + 10)^2} - 36{n^2} = ({n^2} + 10 - 6n)({n^2} + 10 + 6n)\)
Để A là số nguyên tố thì A chỉ có 2 ước là 1 và chính nó.
\(A = ({n^2} + 10 - 6n)({n^2} + 10 + 6n)\) có ước là 1 và chính nó khi và chỉ khi \({n^2} + 10 - 6n = 1\) hoặc \({n^2} + 10 + 6n = 1\).
Trường hợp 1. Với \({n^2} + 10 - 6n = 1\), ta có:
\(\begin{array}{l}{n^2} + 10 - 6n = 1\\{n^2} - 6n + 9 = 0\\{\left( {n - 3} \right)^2} = 0\\n = 3\,(tm)\end{array}\)
Khi đó \(A = 1.\left( {{3^2} + 10 + 6.3} \right) = 37\)
Trường hợp 2. Với \({n^2} + 10 + 6n = 1\), ta có:
\(\begin{array}{l}{n^2} + 10 + 6n = 1\\{n^2} + 6n + 9 = 0\\{\left( {n + 3} \right)^2} = 0\end{array}\)
\(n = - 3\) (không thỏa mãn vì \(n \in \mathbb{N}\)).
Vậy n = 3 thì biểu thức \(A = {({n^2} + 10)^2} - 36{n^2}\) có giá trị là một số nguyên tố.
Phần trắc nghiệm (3 điểm) Câu 1: Kết quả thương của phép chia (left( 3x{{y}^{2}}-2{{x}^{2}}y+{{x}^{3}} right):left( -frac{1}{2}x right)) là :
Phần trắc nghiệm (3 điểm) Câu 1: Kết quả của phép tính (xy + 5)(xy – 1) là:
Phần trắc nghiệm (3 điểm) Câu 1: Thu gọn đa thức (2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y) ta được:
Phần trắc nghiệm (3 điểm) Câu 1: Giá trị của đa thức x2 - y2 - 2y - 1 tại x = 73 và y = 26 là:
A. NỘI DUNG ÔN TẬP Đại số 1. Các phép toán cộng, trừ, nhân, chia đa thức nhiều biến.
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
