-
Toán 9 tập 1 - Cánh diều
-
Toán 9 tập 2 - Cánh diều
Toán 9 cánh diều | Giải toán lớp 9 cánh diều
Bài 5. Độ dài cung tròn, diện tích hình quạt tròn, diện..
Lý thuyết Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên Toán 9 Cánh diều
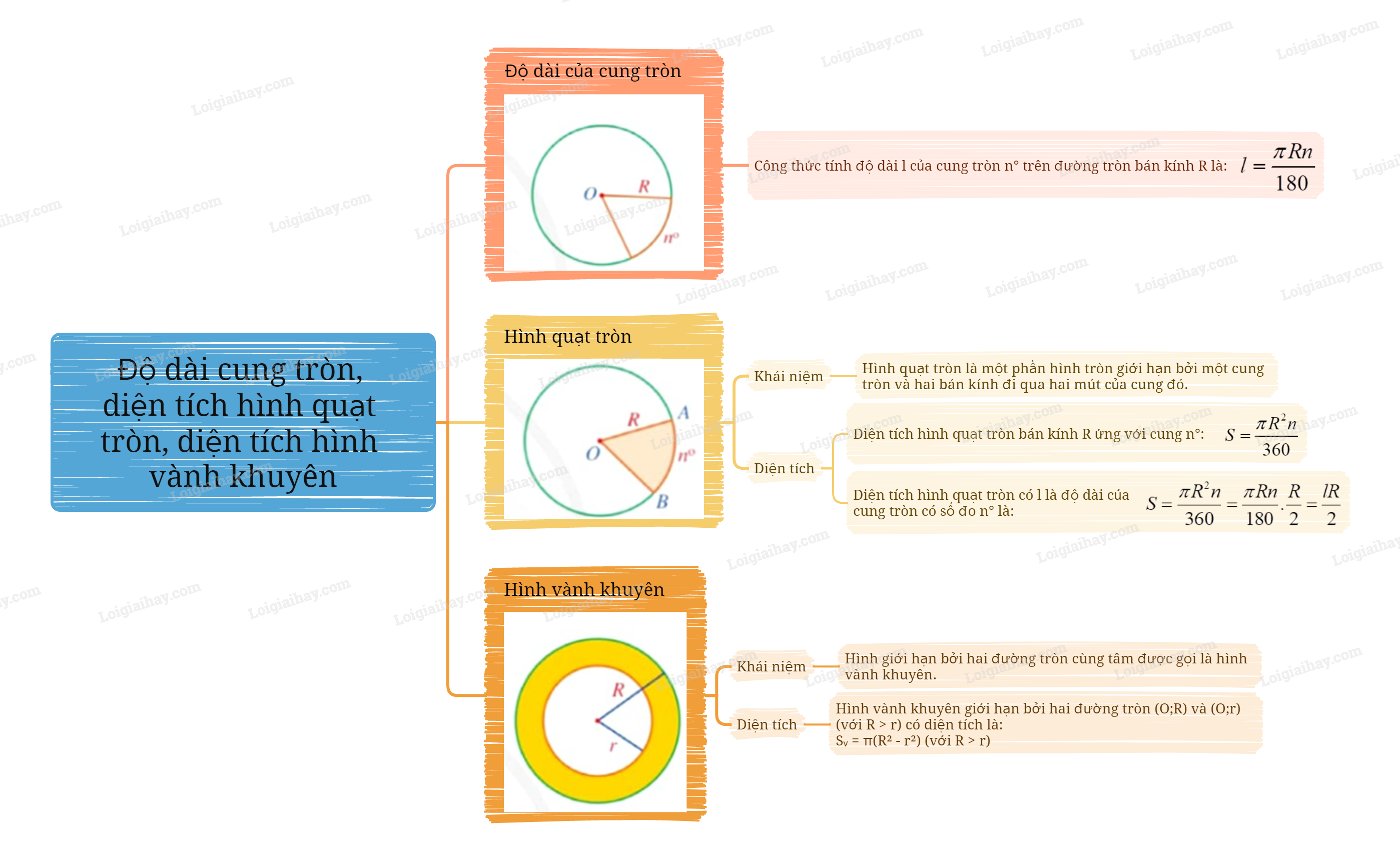
1. Độ dài cung tròn Tỉ số giữa chi vi C của mỗi đường tròn với đường kính d của đường tròn đó là một hằng số, kí hiệu là \(\pi \). Số \(\pi \) là số vô tỉ, cụ thể: \(\pi = 3,1415...\)
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
1. Độ dài cung tròn
Tỉ số giữa chi vi C của mỗi đường tròn với đường kính d của đường tròn đó là một hằng số, kí hiệu là \(\pi \). Số \(\pi \) là số vô tỉ, cụ thể: \(\pi = 3,1415...\)
- Chu vi đường tròn đường kính d là \(C = \pi d\).
- Chu vi đường tròn bán kính R là \(C = 2\pi R\).
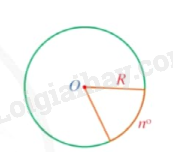
Công thức tính độ dài cung tròn
|
Trong một đường tròn bán kính R, độ dài của cung tròn có số đo \(n^\circ \) là \(l = \frac{{\pi Rn}}{{180}}\). |
Ví dụ:
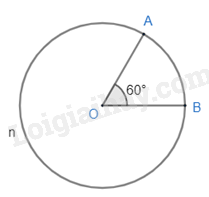
Đường tròn (O; 2cm), \(\widehat {AOB} = 60^\circ \).
- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.
Do đó sđ$\overset\frown{AB}=\widehat{AOB}=60{}^\circ $
Độ dài \({l_1}\) của cung AB là:
\({l_1} = \frac{{\pi Rn}}{{180}} = \frac{{\pi .2.60}}{{180}} = \frac{{2\pi }}{3} \approx 2,1\left( {cm} \right)\)
Cung lớn AnB có số đo là:
sđ$\overset\frown{AmN}=360{}^\circ -60{}^\circ =300{}^\circ $.
Độ dài \({l_2}\) của cung AnB là:
\({l_2} = \frac{{\pi .2.300}}{{180}} = \frac{{10\pi }}{3} \approx 10,5\left( {cm} \right)\)
2. Diện tích hình quạt tròn
Chú ý:
- Hình tròn tâm O bán kính R bao gồm đường tròn (O;R) và tất cả các điểm nằm trong đường tròn đó.
- Diện tích của hình tròn bán kính R là \(S = \pi {R^2}\).
Khái niệm hình quạt tròn
|
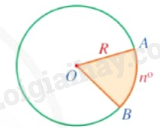
Hình quạt tròn (hay còn gọi tắt là hình quạt) là một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó. |
Diện tích hình quạt tròn
|
Diện tích hình quạt tròn bán kính R ứng với cung \(n^\circ \): \(S = \frac{{\pi {R^2}n}}{{360}}\) |
Nhận xét: Gọi \(l\) là độ dài của cung tròn có số đo \(n^\circ \) thì diện tích hình quạt tròn bán kính R, cung tròn có số đo \(n^\circ \) là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi Rn}}{{180}}.\frac{R}{2} = \frac{{lR}}{2}\).
Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là \(l = 4\pi \)cm, bán kính là R = 5cm là:
\({S_q} = \frac{{l.R}}{2} = \frac{{4\pi .5}}{2} = 10\pi \left( {c{m^2}} \right)\)
3. Diện tích hình vành khuyên
Khái niệm hình vành khuyên
|
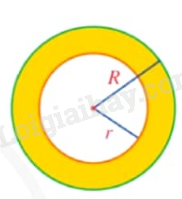
Hình giới hạn bởi hai đường tròn cùng tâm được gọi là hình vành khuyên. |
Diện tích hình vành khuyên
|
Hình vành khuyên giới hạn bởi hai đường tròn (O;R) và (O;r) (với R > r) có diện tích là: |
|
\(S = \pi \left( {{R^2} - {r^2}} \right)\). |
Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:
\({S_v} = \pi \left( {{5^2} - {3^2}} \right) = 16\pi \left( {{m^2}} \right)\)
Bình luận
Chia sẻ
- Giải mục 1 trang 118, 119 SGK Toán 9 tập 1 - Cánh diều
- Giải mục 2 trang 119, 120, 121 SGK Toán 9 tập 1 - Cánh diều
- Giải mục 3 trang 122 SGK Toán 9 tập 1 - Cánh diều
- Giải bài tập 1 trang 122 SGK Toán 9 tập 1 - Cánh diều
- Giải bài tập 2 trang 123 SGK Toán 9 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
