Lý thuyết Bất phương trình bậc nhất một ẩn Toán 9 Kết nối tri thức

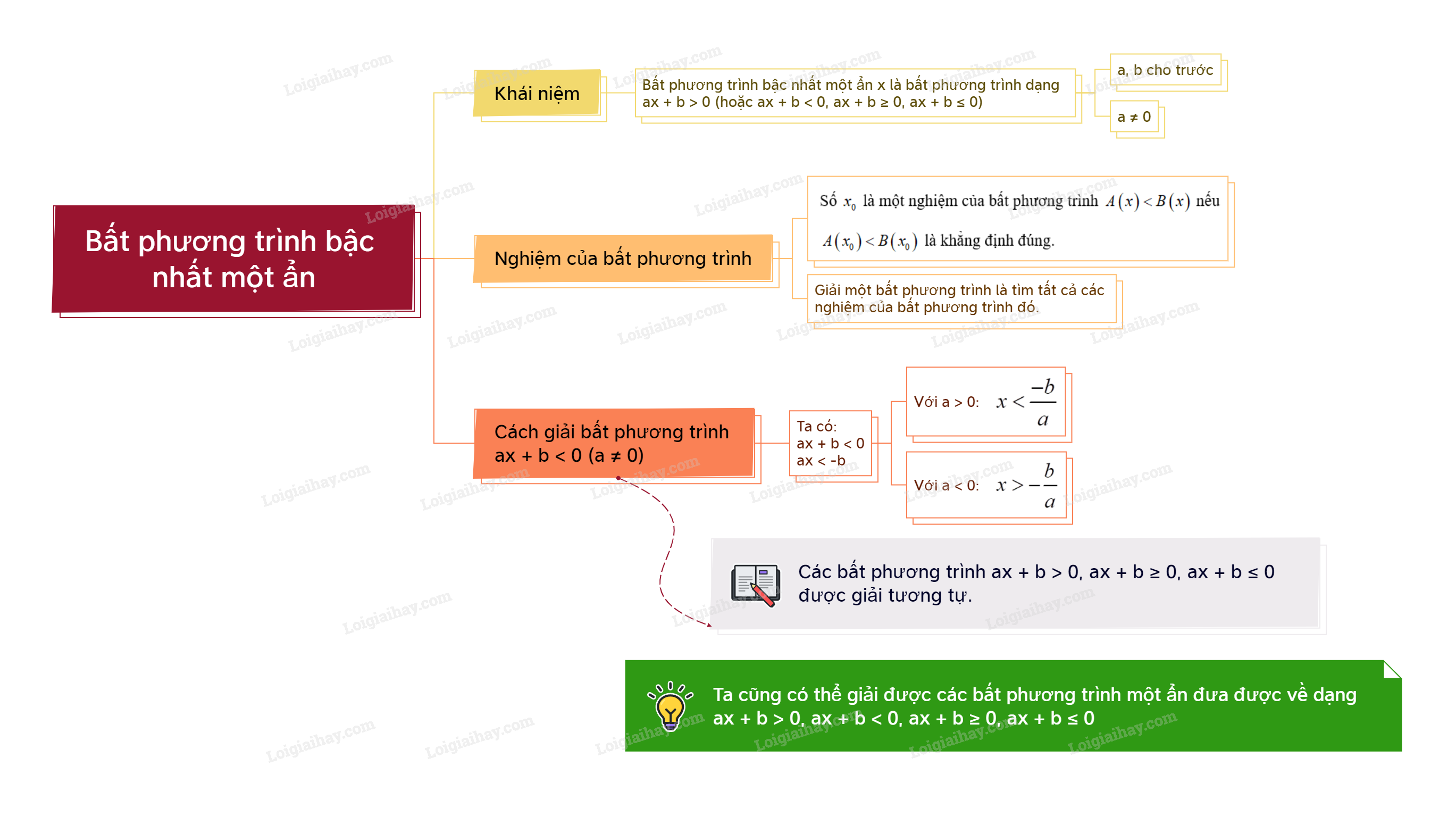
1. Khái niệm bất phương trình bậc nhất một ẩn Khái niệm bất phương trình bậc nhất một ẩn

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

1. Khái niệm bất phương trình bậc nhất một ẩn

Khái niệm bất phương trình bậc nhất một ẩn

Bất phương trình dạng \(ax + b < 0\) (hoặc \(ax + b > 0\); \(ax + b \le 0\); \(ax + b \ge 0\)) trong đó a, b là hai số đã cho, \(a \ne 0\) được gọi là bất phương trình bậc nhất một ẩn x.

Ví dụ: \(3x + 16 \le 0\); \( - 3x > 0\) là các bất phương trình bậc nhất một ẩn x.

\({x^2} - 4 \ge 0\) không phải là một bất phương trình bậc nhất một ẩn x vì \({x^2} - 4\) là một đa thức bậc hai.

\(3x - 2y < 2\) không phải là một bất phương trình bậc nhất một ẩn vì đa thức \(3x - 2y\) là đa thức với hai biến x và y.

Nghiệm của bất phương trình

- Số \({x_0}\) là một nghiệm của bất phương trình \(A\left( x \right) < B\left( x \right)\) nếu \(A\left( {{x_0}} \right) < B\left( {{x_0}} \right)\) là khẳng định đúng.

- Giải một bất phương trình là tìm tất cả các nghiệm của bất phương trình đó.

Ví dụ:

Số -2 là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.\left( { - 2} \right) - 10 = - 4 - 10 = - 14 < 0\).

Số 6 không là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.6 - 10 = 12 - 10 = 2 > 0\).

2. Cách giải bất phương trình bậc nhất một ẩn

Bất phương trình bậc nhất một ẩn \(ax + b < 0\left( {a \ne 0} \right)\) được giải như sau:

\(\begin{array}{l}ax + b < 0\\ax < - b\end{array}\)

- Nếu \(a > 0\) thì \(x < \frac{{ - b}}{a}\).

- Nếu \(a < 0\) thì \(x > - \frac{b}{a}\).

Chú ý: Các bất phương trình \(ax + b > 0\), \(ax + b \le 0\), \(ax + b \ge 0\) được giải tương tự.

Ví dụ: Giải bất phương trình \( - 2x - 4 > 0\)

Lời giải: Ta có:

\(\begin{array}{l} - 2x - 4 > 0\\ - 2x > 0 + 4\\ - 2x > 4\\x < 4.\left( { - \frac{1}{2}} \right)\\x < - 2\end{array}\)

Vậy nghiệm của bất phương trình là \(x < - 2\).

Chú ý: Ta cũng có thể giải được các bất phương trình một ẩn đưa được về dạng \(ax + b < 0\), \(ax + b > 0\), \(ax + b \le 0\), \(ax + b \ge 0\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 39 SGK Toán 9 tập 1 - Kết nối tri thức
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn x? a) ( - 3x + 7 le 0;) b) (4x - frac{3}{2} > 0;) c) ({x^3} > 0.)
Giải mục 2 trang 39, 40, 41 SGK Toán 9 tập 1 - Kết nối tri thức
Xét bất phương trình (5x + 3 < 0.left( 1 right)) Hãy thực hiện các yêu cầu sau để giải bất phương trình (1): a) Sử dụng tính chất của bất đẳng thức, cộng vào hai vế của bất phương trình (1) với -3, ta được một bất phương trình, kí hiệu là (2). b) Sử dụng tính chất của bất đẳng thức, nhân vào hai vế của bất phương trình (2) với (frac{1}{5}) (tức là chia cả hai vế của bất phương trình (2) cho hệ số của x là 5) để tìm nghiệm của bất phương trình.
Giải bài tập 2.16 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các bất phương trình sau: a) (x - 5 ge 0;) b) (x + 5 le 0;) c) ( - 2x - 6 > 0;) d) (4x - 12 < 0.)
Giải bài tập 2.17 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức
Giải các bất phương trình sau: a) (3x + 2 > 2x + 3;) b) (5x + 4 < - 3x - 2.)
Giải bài tập 2.18 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức
Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 1 tháng là 0,4%. Hỏi nếu muốn có số tiền lãi hàng tháng ít nhất là 3 triệu đồng thì số tiền gửi lãi tiết kiệm ít nhất là bao nhiêu (làm tròn đến triệu đồng)?
Giải bài tập 2.19 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức
Một ngân hàng đang áp dụng lãi suất gửi tiết kiệm kì hạn 1 tháng là 0,4%. Hỏi nếu muốn có số tiền lãi hàng tháng ít nhất là 3 triệu đồng thì số tiền gửi lãi tiết kiệm ít nhất là bao nhiêu (làm tròn đến triệu đồng)?
Giải bài tập 2.20 trang 41 SGK Toán 9 tập 1 - Kết nối tri thức
Người ta dùng một loại xe tải để chở sữa tươi cho một nhà máy. Biết mỗi thùng sữa loại 180 ml nặng trung bình 10 kg. Theo khuyến nghị, trọng tải của xe (tức là tổng khối lượng tối đa cho phép mà xe có thể chở) là 5,25 tấn. Hỏi xe có thể chở tối đa bao nhiêu thùng bia, biết bác lái xe nặng 65kg?