 Giải Toán lớp 5 Kết nối tri thức, giải SGK toán lớp 5 KNTT
Giải Toán lớp 5 Kết nối tri thức, giải SGK toán lớp 5 KNTT
 Chủ đề 9. Diện tích và thể tích của một số hình khối SG..
Chủ đề 9. Diện tích và thể tích của một số hình khối SG.. Toán lớp 5 Bài 55. Luyện tập chung - SGK Kết nối tri thức với cuộc sống
Chọn câu trả lời đúng. Mai có thể gấp hình khai triển ở trên thành chiếc hộp nào? Hoàn thành bảng sau. Nam làm một chiếc hộp từ hình khai triển dưới đây. Việt có một chiếc hộp gỗ (có nắp) dạng hình hộp chữ nhật có chiều dài 25 cm, chiều rộng 20 cm và chiều cao 10 cm. Việt đã sơn màu nâu lên các mặt xung quanh và màu vàng lên 2 mặt đáy của chiếc hộp đó. Tính diện tích phần được sơn màu nâu.
Luyện tập 1 Câu 1
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 60 SGK Toán 5 Kết nối tri thức
Chọn câu trả lời đúng.

Mai có thể gấp hình khai triển ở trên thành chiếc hộp nào?

Phương pháp giải:
Quan sát hình khai triển và chọn đáp án đúng.
Lời giải chi tiết:
Chọn đáp án B.
Luyện tập 1 Câu 2
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 60 SGK Toán 5 Kết nối tri thức
Hoàn thành bảng sau.

Phương pháp giải:
- Diện tích xung quanh của hình lập phương bằng diện tích một mặt nhân với 4.
- Diện tích toàn phần của hình lập phương bằng diện tích một mặt nhân với 6.
Lời giải chi tiết:

Luyện tập 1 Câu 3
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 60 SGK Toán 5 Kết nối tri thức
Nam làm một chiếc hộp từ hình khai triển dưới đây.
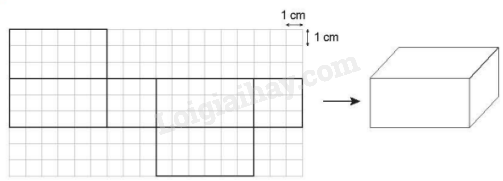
Tính thể tích của chiếc hộp đó.
Phương pháp giải:
- Quan sát hình khai triển của chiếc hộp để biết chiều dài, chiều rộng, chiều cao chiếc hộp có dạng hình hộp chữ nhật.
- Thể tích hình hộp chữ nhật = chiều dài x chiều rộng x chiều cao (cùng đơn vị đo).
Lời giải chi tiết:
Quan sát hình khai triển của chiếc hộp ta thấy chiếc hộp có chiều dài 6 cm, chiều rộng 3 cm, chiều cao 3 cm.
Thể tích hình hộp chữ nhật là:
6 x 3 x 3 = 54 (cm3)
Đáp số: 54 cm3
Luyện tập 1 Câu 4
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 61 SGK Toán 5 Kết nối tri thức
Việt có một chiếc hộp gỗ (có nắp) dạng hình hộp chữ nhật có chiều dài 25 cm, chiều rộng 20 cm và chiều cao 10 cm. Việt đã sơn màu nâu lên các mặt xung quanh và màu vàng lên 2 mặt đáy của chiếc hộp đó. Tính diện tích phần được sơn màu nâu.

Phương pháp giải:
- Diện tích phần được sơn màu nâu bằng diện tích xung quanh của chiếc hộp gỗ có dạng hình hộp chữ nhật.
- Diện tích xung quang của hình hộp chữ nhật = chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
Lời giải chi tiết:
Diện tích phần được sơn màu nâu là:
(25 + 20) x 2 x 10 = 900 (cm2)
Đáp số: 900 cm2
Câu 1
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 61 SGK Toán 5 Kết nối tri thức
Chọn câu trả lời đúng.
Hình nào dưới đây là hình khai triển của một hình hộp chữ nhật?
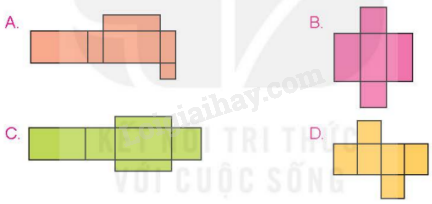
Phương pháp giải:
Quan sát hình khai triển và chọn đáp án đúng.
Lời giải chi tiết:
Chọn đáp án D.
Luyện tập 2 Câu 2
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 61 SGK Toán 5 Kết nối tri thức
Tính thể tích của mỗi hình dưới đây.

Phương pháp giải:
- Muốn tính thể tích của hình hộp chữ nhật, ta lấy chiều dài nhân chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).
- Muốn tính thể tích của hình lập phương, ta lấy cạnh nhân với cạnh rồi nhân với cạnh.
Lời giải chi tiết:
a) Thể tích hình hộp chữ nhật là:
2 x 1 x 1,5 = 3 (dm3)
b) Thể tích hình lập phương là:
15 x 15 x 15 = 3 375 (cm3)
Đáp số: a) 3 dm3
b) 3 375 cm3
Luyện tập 2 Câu 3
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 62 SGK Toán 5 Kết nối tri thức
Một bể bơi dạng hình hộp chữ nhật có chiều dài 25 m, chiều rộng 8 m và sâu 1,4 m. Người ta lát ở đáy và xung quanh hồ bơi bằng những viên gạch hoa. Tính diện tích lát gạch.
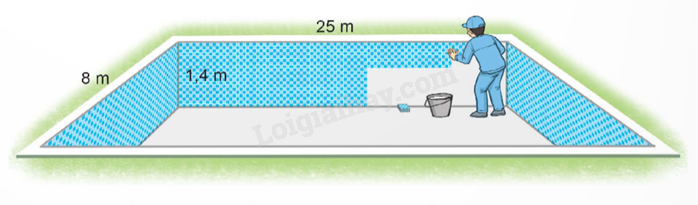
Phương pháp giải:
- Diện tích phần lát gạch = diện tích xung quanh của bể bơi dạng hình hộp chữ nhật.
- Diện tích xung quang của hình hộp chữ nhật = chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
Lời giải chi tiết:
Diện tích lát gạch là:
(25 + 8) x 2 x 1,4 = 92,4 (m2)
Diện tích đáy bể bơi là:
25 x 8 = 200 (m2)
Diện tích lát gạch là:
92,4 + 200 = 292,4 (m2)
Đáp số: 292,4 m2
Luyện tập 2 Câu 4
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 62 SGK Toán 5 Kết nối tri thức
Chú Tư xếp các hộp đựng loa lên xe tải có kích thước thùng xe như trong hình vẽ. Biết các hộp đều có dạng hình hộp chữ nhật với chiều dài 0,5 m, chiều rộng 0,4 m và chiều cao 0,3 m. Hỏi chú Tư có thể xếp được 64 hộp như vậy lên thùng xe hay không?
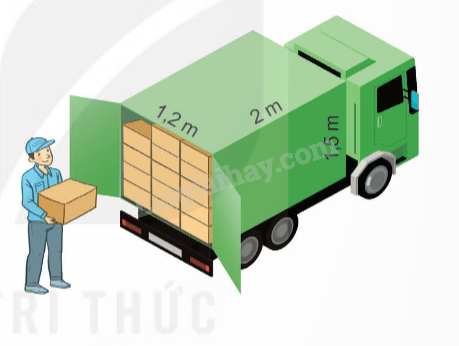
Phương pháp giải:
- Tính thể tích mỗi hộp hình chữ nhật = chiều dài x chiều rộng x chiều cao.
- Tính thể tích thùng xe = chiều dài x chiều rộng x chiều cao.
- Số hộp xếp được vào thùng xe = thể tích thùng xe : thể tích mỗi hộp.
Lời giải chi tiết:
Thể tích mỗi hộp hình chữ nhật là:
0,5 x 0,4 x 0,3 = 0,06 (m3)
Thể tích thùng xe là:
2 x 1,2 x 1,5 = 3,6 (m3)
Số hộp xếp được vào thùng xe là:
3,6 : 0,06 = 60 (hộp)
Vậy chú Tư không thể xếp được 64 hộp như vậy lên thùng xe.
Luyện tập 3 Câu 1
Video hướng dẫn giải
Trả lời câu hỏi 1 trang 62 SGK Toán 5 Kết nối tri thức
Chọn câu trả lời đúng.
Mai có hình khai triển như hình bên.
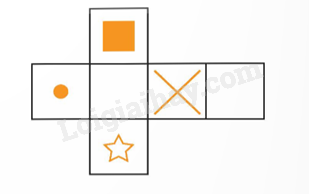
Hỏi Mai có thể gấp được hình lập phương nào dưới đây?

Phương pháp giải:
Quan sát hình khai triển và chọn đáp án đúng.
Lời giải chi tiết:
Chọn đáp án B.
Luyện tập 3 Câu 2
Video hướng dẫn giải
Trả lời câu hỏi 2 trang 63 SGK Toán 5 Kết nối tri thức
Chú Nhân vừa hoàn thành mô hình quả bóng bằng các miếng gỗ. Chú muốn làm một chiếc hộp hình lập phương bằng nhựa cứng cạnh 2,5 dm để bảo quản quả bóng. Tính diện tích nhựa cứng mà chú cần dùng để làm chiếc hộp đó.
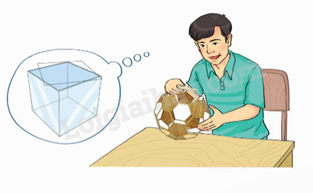
Phương pháp giải:
- Diện tích nhựa cứng để làm chiếc hộp = diện tích toàn phần của chiếc hộp có dạng hình lập phương.
- Diện tích toàn phần của hình lập phương = diện tích một mặt x 6
Lời giải chi tiết:
Diện tích nhựa cứng mà chú cần dùng để làm chiếc hộp là:
2,5 x 2,5 x 6 = 37,5 (dm2)
Đáp số: 37,5 dm2
Luyện tập 3 Câu 3
Video hướng dẫn giải
Trả lời câu hỏi 3 trang 63 SGK Toán 5 Kết nối tri thức
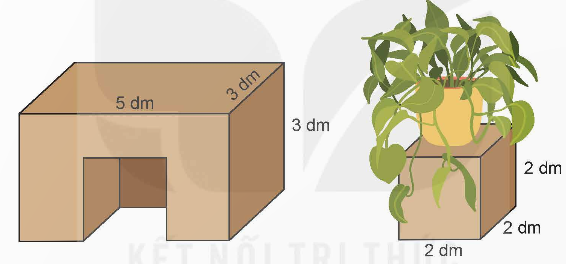
Bác thợ mộc có một khối gỗ dạng hình hộp chữ nhật với kích thước như hình vẽ dưới đây. Bác cắt đi một phần gỗ có dạng hình lập phương cạnh 2 dm để làm đế đỡ chậu cây và phần còn lại dùng làm ghế. Tính thể tích phần khối gỗ dùng làm ghế.
Phương pháp giải:
- Tính thể tích khối gỗ dạng hình hộp chữ nhật ban đầu = chiều dài x chiều rộng x chiều cao.
- Tính thể tích phần khối gỗ hình lập phương = cạnh x cạnh x cạnh.
- Thể tích khối gỗ dùng làm ghế = thể tích khối gỗ dạng hình chữ nhật - thể tích phần khối gỗ hình lập phương.
Lời giải chi tiết:
Thể tích khối gỗ dạng hình hộp chữ nhật là:
3 x 5 x 3 = 45 (dm3)
Thể tích phần khối gỗ hình lập phương là:
2 x 2 x 2 = 8 (dm3)
Thể tích khối gỗ dùng làm ghế là:
45 – 8 = 37 (dm3)
Đáp số: 37 dm3
Luyện tập 3 Câu 4
Video hướng dẫn giải
Trả lời câu hỏi 4 trang 63 SGK Toán 5 Kết nối tri thức
Số?
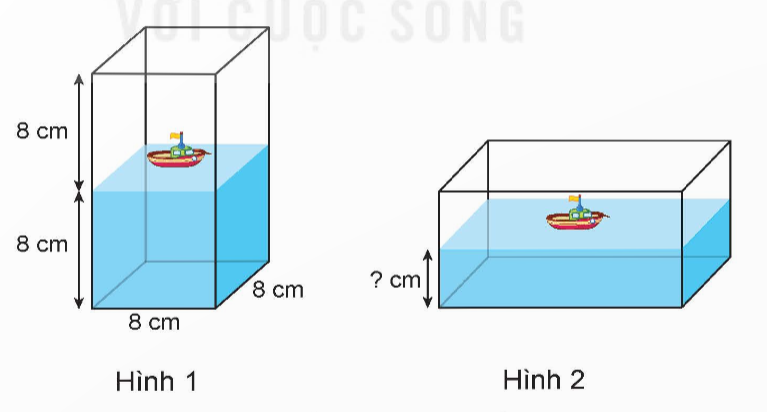
Khi đặt hộp đứng như hình 1, phần nước có chiều cao là 8 cm.
Vậy khi xoay hộp đó như hình 2 thì phần nước có chiều cao là ? cm.
Phương pháp giải:
- Thể tích phần nước khi đặt hộp đứng = diện tích mặt đáy x chiều cao.
- Thể tích phần nước khi đặt hộp xoay = thể tích phần nước khi đặt hộp đứng.
- Chiều cao phần nước khi xoay hộp = thể tích phần nước khi đặt hộp xoay : diện tích mặt đáy.
Lời giải chi tiết:
Thể tích phần nước khi đặt hộp đứng là:
8 x 8 x 8 = 512 (cm3)
Diện tích mặt đáy khi đặt hộp xoay là:
8 x 16 = 128 (cm2)
Chiều cao phần nước khi xoay hộp là:
512 : 128 = 4 (cm)
Vậy khi xoay hộp đó như hình 2 thì phần nước có chiều cao là 4 cm.
- Toán lớp 5 Bài 54. Thực hành tính toán và ước lượng thể tích một số hình khối - SGK Kết nối tri thức với cuộc sống
- Toán lớp 5 Bài 53.Thể tích của hình lập phương - SGK Kết nối tri thức với cuộc sống
- Toán lớp 5 Bài 52. Thể tích của hình hộp chữ nhật - SGK Kết nối tri thức với cuộc sống
- Toán lớp 5 Bài 51. Diện tích xung quanh và diện tích toàn phần của hình lập phương - SGK Kết nối tri thức với cuộc sống
- Toán lớp 5 Bài 50. Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật - SGK Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán lớp 5 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Nhân, chia số thập phân với 10; 100; 1 000; ... Hoặc với 0,1; 0,01; 0,001;... - Toán 5 Kết nối tri thức
- Lý thuyết Hình tam giác. Diện tích hình tam giác - Toán 5 Kết nối tri thức
- Lý thuyết Hình thang. Diện tích hình thang - Toán 5 Kết nối tri thức
- Lý thuyết Đường tròn. Chu vi và diện tích hình tròn - Toán 5 Kết nối tri thức
- Lý thuyết Phép trừ hai số thập phân - Toán 5 Kết nối tri thức
- Lý thuyết Đường tròn. Chu vi và diện tích hình tròn - Toán 5 Kết nối tri thức
- Lý thuyết Hình thang. Diện tích hình thang - Toán 5 Kết nối tri thức
- Lý thuyết Hình tam giác. Diện tích hình tam giác - Toán 5 Kết nối tri thức
- Lý thuyết Nhân, chia số thập phân với 10; 100; 1 000; ... Hoặc với 0,1; 0,01; 0,001;... - Toán 5 Kết nối tri thức
- Lý thuyết Phép chia số thập phân- Toán 5 Kết nối tri thức












Danh sách bình luận