Giải Toán lớp 5 Kết nối tri thức, giải SGK toán lớp 5 KNTT

Chủ đề 9. Diện tích và thể tích của một số hình khối SG..

Toán lớp 5 Bài 50. Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật - SGK Kết nối tri thức với cuộc sống

Tính diện tích xung quanh của hình hộp chữ nhật có: a) Chiều dài 7 dm, chiều rộng 5 dm và chiều cao 4 dm. b) Chiều dài 6,5 cm, chiều rộng 3,5 cm và chiều cao 5 cm. Một bể bơi dạng hình hộp chữ nhật có chiều dài 10 m, chiều rộng 4 m và sâu 1,5 m. Người ra muốn ốp gạch men xung quanh thành bể bơi. Tính phần diện tích được ốp gạch men (diện tích mạch vữa không đáng kể). Tính diện tích toàn phần của mỗi hình hộp chữ nhật dưới đây.

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 1
- Câu 1
- Câu 2
Hoạt động 2
- Câu 1
- Câu 2
Luyện tập
- Câu 1
- Câu 2
- Câu 3
- Câu 4

Hoạt động 1 Câu 1

Trả lời câu hỏi 1 trang 45 SGK Toán 5 Kết nối tri thức

Tính diện tích xung quanh của hình hộp chữ nhật có:

a) Chiều dài 7 dm, chiều rộng 5 dm và chiều cao 4 dm.

b) Chiều dài 6,5 cm, chiều rộng 3,5 cm và chiều cao 5 cm.

Phương pháp giải:

Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).

Lời giải chi tiết:

a) Diện tích xung quanh của hình hộp chữ nhật là:

(7 + 5) x 2 x 4 = 96 (dm²)

Đáp số: 96 dm²

b) Diện tích xung quanh của hình hộp chữ nhật là:

(6,5 + 3,5) x 2 x 5 = 100 (cm²)

Đáp số: 100 cm²

Hoạt động 1 Câu 2

Trả lời câu hỏi 2 trang 45 SGK Toán 5 Kết nối tri thức

Một bể bơi dạng hình hộp chữ nhật có chiều dài 10 m, chiều rộng 4 m và sâu 1,5 m. Người ra muốn ốp gạch men xung quanh thành bể bơi. Tính phần diện tích được ốp gạch men (diện tích mạch vữa không đáng kể).

Phương pháp giải:

- Phần diện tích được ốp gạch men = diện tích xung quanh của bể bơi dạng hình hộp chữ nhật.

- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).

Lời giải chi tiết:

Phần diện tích được ốp gạch men là:

(10 + 4) x 2 x 1,5 = 42 (m²)

Đáp số: 42 m²

Hoạt động 2 Câu 1

Trả lời câu hỏi 1 trang 46 SGK Toán 5 Kết nối tri thức

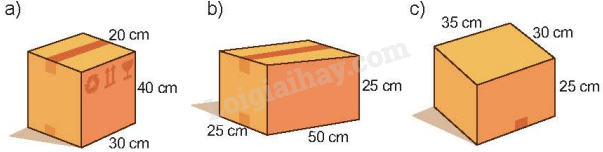
Tính diện tích toàn phần của mỗi hình hộp chữ nhật dưới đây.

Phương pháp giải:

Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

Lời giải chi tiết:

Diện tích xung quanh của hình hộp chữ nhật là:

(30 + 20) x 2 x 40 = 4 000 (cm²)

Diện tích hai đáy của hình hộp chữ nhật là:

30 x 20 x 2 = 1 200 (cm²)

Diện tích toàn phần của hình hộp chữ nhật là:

4 000 + 1 200 = 5 200 (cm²)

Đáp số: 5 200 cm²

Diện tích xung quanh của hình hộp chữ nhật là:

(50 + 25) x 2 x 25 = 3 750 (cm²)

Diện tích hai đáy của hình hộp chữ nhật là:

50 x 25 x 2 = 2 500 (cm²)

Diện tích toàn phần của hình hộp chữ nhật là:

3 750 + 2 500 = 6 250 (cm²)

Đáp số: 6 250 cm²

Diện tích xung quanh của hình hộp chữ nhật là:

(35 +30) x 2 x 25 = 3 250 (cm²)

Diện tích hai đáy của hình hộp chữ nhật là:

35 x 30 x 2 = 2 100 (cm²)

Diện tích toàn phần của hình hộp chữ nhật là:

3 250 + 2 100 = 5 350 (cm²)

Đáp số: 5 350 cm²

Hoạt động 2 Câu 2

Trả lời câu hỏi 2 trang 46 SGK Toán 5 Kết nối tri thức

Chọn câu trả lời đúng.

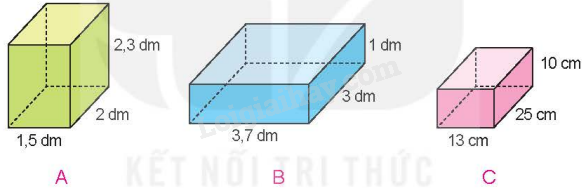
Chiếc hộp nào dưới đây có diện tích toàn phần lớn nhất?

Phương pháp giải:

- Tính diện tích toàn phần của từng chiếc hộp

- So sánh diện tích toàn phần của từng chiếc hộp và chọn chiếc hộp có diện tích toàn phần lớn nhất.

- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

Lời giải chi tiết:

Hình A.

Diện tích xung quanh của chiếc hộp là:

(2 + 1,5) x 2 x 2,3 = 16,1 (dm²)

Diện tích hai đáy của hình hộp chữ nhật là:

2 x 1,5 x 2 = 6 (dm²)

Diện tích toàn phần của hình hộp chữ nhật là:

16,1 + 6 = 22,1 (cm²)

Hình B.

Diện tích xung quanh của chiếc hộp là:

(3,7 + 3) x 2 x 1 = 13,4 (dm²)

Diện tích hai đáy của hình hộp chữ nhật là:

3,7 x 3 x 2 = 22,2 (dm²)

Diện tích toàn phần của hình hộp chữ nhật là:

13,4 + 22,2 = 35,6 (dm²)

Hình C.

Diện tích xung quanh của chiếc hộp là:

(25 + 13) x 2 x 10 = 760 (cm²)

Diện tích hai đáy của hình hộp chữ nhật là:

25 x 13 x 2 = 650 (cm²)

Diện tích toàn phần của hình hộp chữ nhật là:

760 + 650 = 1 410 (cm²)

Đổi: 1 410 cm² = 14,1 dm²

Ta có: 14,1 dm² < 22,1 dm² < 35,6 dm²

Vậy chiếc hộp B có diện tích toàn phần lớn nhất.

Chọn B.

Luyện tập Câu 1

Trả lời câu hỏi 1 trang 46 SGK Toán 5 Kết nối tri thức

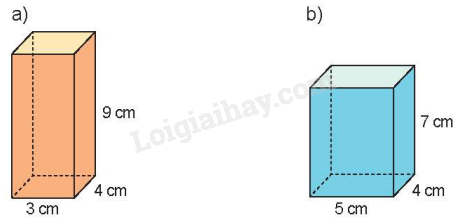
Tính diện tích xung quanh của mỗi hình hộp chữ nhật dưới đây.

Phương pháp giải:

Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).

Lời giải chi tiết:

a) Diện tích xung quanh của hình hộp chữ nhật là:

(4 + 3) x 2 x 9 = 126 (cm²)

Đáp số: 126 cm²

b) Diện tích xung quanh của hình hộp chữ nhật là:

(5 + 4) x 2 x 7 = 126 (cm²)

Đáp số: 126 cm²

Luyện tập Câu 2

Trả lời câu hỏi 2 trang 47 SGK Toán 5 Kết nối tri thức

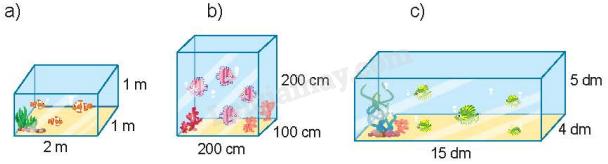
Các bể cá dưới đây được làm bằng kính và thiết kế dạng hình hộp chữ nhật không có nắp. Hãy tính diện tích kính được sử dụng để làm các bể cá đó.

Phương pháp giải:

Bể cá dạng hình hộp chữ nhật không có nắp nên diện tích kính được sử dụng bằng diện tích xung quanh cộng với diện tích một mặt đáy của bể.

Lời giải chi tiết:

Diện tích xung quanh của bể cá là:

(2 + 1) x 2 x 1 = 6 (m²)

Diện tích một mặt đáy của bể cá là:

2 x 1 = 2 (m²)

Diện tích kính được sử dụng làm bể cá là:

6 + 2 = 8 (m²)

Đáp số: 8 m²

Diện tích xung quanh của bể cá là:

(200 + 100) x 2 x 200 = 120 000 (cm²)

Diện tích một mặt đáy của bể cá là:

200 x 100 = 20 000 (cm²)

Diện tích kính được sử dụng làm bể cá là:

120 000 + 20 000 = 140 000 (cm²)

Đáp số: 140 000 cm²

Diện tích xung quanh của bể cá là:

(15 + 4) x 2 x 5 = 190 (dm²)

Diện tích một mặt đáy của bể cá là:

15 x 4 = 60 (dm²)

Diện tích kính được sử dụng làm bể cá là:

190 + 60 = 250 (dm²)

Đáp số: 250 dm²

Luyện tập Câu 3

Trả lời câu hỏi 3 trang 47 SGK Toán 5 Kết nối tri thức

Mỗi khuôn bánh chưng có dạng một hình hộp chữ nhật không có hai đáy như hình bên.

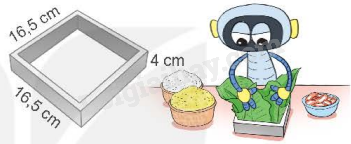
Hỏi từ thanh gỗ dưới đây có thể làm được khuôn bánh chưng với kích thước như trên hay không?

Phương pháp giải:

- Tính diện tích xung quanh của khuôn bánh chưng có dạng hình hộp chữ nhật

- Tính diện tích thanh gỗ.

- So sánh diện tích xung quanh của khuôn bánh chưng và diện tích thanh gỗ rồi đưa ra kết luận.

Lời giải chi tiết:

Diện tích xung quanh của khuôn bánh chưng có dạng hình hộp chữ nhật là:

(16,5 + 16,5) x 2 x 4 = 264 (cm²)

Diện tích thanh gỗ là:

55 x 4 = 220 (cm²)

Vì 220 cm² < 264 cm² nên thanh gỗ không thể làm được khuôn bánh chưng.

Luyện tập Câu 4

Trả lời câu hỏi 4 trang 47 SGK Toán 5 Kết nối tri thức

Mỗi bạn Mai, Việt, Nam dùng bốn hình lập phương nhỏ như nhau có độ dài cạnh là 1 dm và xếp được các hình dưới đây.

Hỏi bạn nào xếp được hình hộp chữ nhật có:

a) Diện tích xung quanh lớn nhất?

b) Diện tích toàn phần bé nhất?

Phương pháp giải:

Quan sát hình vẽ để tìm số đo chiều dài, chiều rộng, chiều cao của từng hình.

a) Tính diện tích xung quanh của mỗi hình và so sánh.

b) Tính diện tích toàn phần của mỗi hình và so sánh.

Lời giải chi tiết:

Bạn Mai xếp các hình lập phương thành hình hộp chữ nhật có đáy là hình vuông cạnh 1 dm và chiều cao 4 dm.

Bạn Việt xếp các hình lập phương thành hình hộp chữ nhật có chiều dài 4 dm, chiều rộng 1 dm và chiều cao 1 dm.

Bạn Nam xếp các hình lập phương thành hình hộp chữ nhật có đáy là hình vuông cạnh 2 dm và chiều cao 1 dm.

Diện tích xung quanh của hình hộp chữ nhật do bạn Mai xếp là:

(1 + 1) x 2 x 4 = 16 (dm²)

Diện tích xung quanh của hình hộp chữ nhật do bạn Việt xếp là:

(4 + 1) x 2 x 1 = 10 (dm²)

Diện tích xung quanh của hình hộp chữ nhật do bạn Nam xếp là:

(2 + 2) x 2 x 1 = 8 (dm²)

Vì 8 dm² < 10 dm² < 16 dm² nên hình hộp chữ nhật do bạn Mai xếp có diện tích xung quanh lớn nhất.

Diện tích hai mặt đáy của hình hộp chữ nhật do bạn Mai xếp là:

1 x 1 x 2 = 2 (dm²)

Diện tích toàn phần của hình hộp chữ nhật do bạn Mai xếp là:

16 + 2 = 18 (dm²)

Diện tích hai mặt đáy của hình hộp chữ nhật do bạn Việt xếp là:

4 x 1 x 2 = 8 (dm²)

Diện tích toàn phần của hình hộp chữ nhật do bạn Việt xếp là:

10 + 8 = 18 (dm²)

Diện tích hai mặt đáy của hình hộp chữ nhật do bạn Nam xếp là:

2 x 2 x 2 = 8 (dm²)

Diện tích xung quanh của hình hộp chữ nhật do bạn Nam xếp là:

8 + 8 = 16 (dm²)

Vì 18 dm² > 16 dm² nên hình hộp chữ nhật do bạn Nam xếp có diện tích toàn phần bé nhất.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Toán lớp 5 Bài 51. Diện tích xung quanh và diện tích toàn phần của hình lập phương - SGK Kết nối tri thức với cuộc sống
Tính diện tích xung quanh của hình lập phương có độ dài cạnh là: Cửa hàng bánh ngọt thường bảo quản bánh bằng cách cuốn một lớp túi bóng trong suốt vừa đủ quanh Người ta cần dán các mảnh nhựa màu vừa đủ vào khung của những chiếc đèn hình lập phương như hình dưới đây. Hãy tính diện tích các mảnh nhựa màu cần sử dụng cho mỗi bóng đèn. Mai muốn phủ các mặt xung quanh và mặt trên cùng của một chiếc bánh có dạng hình lập
Toán lớp 5 Bài 52. Thể tích của hình hộp chữ nhật - SGK Kết nối tri thức với cuộc sống
Tính thể tích hình hộp chữ nhật có chiều dài 8 cm, chiều rộng 5 cm và chiều cao 6 cm. Bố của Mai vừa làm một bể cá dạng hình chữ nhật với kích thước như hình dưới đây. Tính thể tích của bể cá đó. Số? Việt tạo một khối hình bằng cách ghép 6 hình hộp chữ nhật như hình dưới đây. Biết mỗi hình hộp chữ nhật có chiều dài 10 cm, chiều rộng 5 cm và chiều cao 2 cm. Chọn câu trả lời đúng.
Toán lớp 5 Bài 53.Thể tích của hình lập phương - SGK Kết nối tri thức với cuộc sống
Số? Một chiếc bánh bông lan hình hộp chữ nhật có đáy là hình vuông cạnh 12 cm, chiều cao 6 cm. Chọn câu trả lời đúng. Mai và Rô-bốt xếp được hai hình từ các hình lập phương nhỏ như hình sau. a) Mai cần bỏ đi bao nhiêu hình lập phương nhỏ để nhận được hình như của Rô-bốt? b) Nếu mỗi hình lập phương có cạnh 2 cm thì thể tích hình của Rô-bốt là bao nhiêu xăng-ti-mét Khối ru-bích của Việt có dạng hình lập phương cạnh 6 cm. Thể ti
Toán lớp 5 Bài 54. Thực hành tính toán và ước lượng thể tích một số hình khối - SGK Kết nối tri thức với cuộc sống
Công ty của mẹ Mai đặt mua 100 chậu cây tái chế của lớp 5A để làm quà tặng cho mỗi nhân viên nhân ngày Môi trường Thế giới. Lớp 5A đã chọn mẫu hộp dạng hình lập phương cạnh 2 dm như hình bên để đựng mỗi chậu cây. a) Tính thể tích của mẫu hộp đó. b) Các bạn lớp 5A dự định xếp các hộp đó vào thùng để thuận tiện cho việc vận chuyển. Quan sát kích thước thùng và ước lượng số hộp có thể xếp vào 1 thùng. Em hãy ước lượng chiề
Toán lớp 5 Bài 55. Luyện tập chung - SGK Kết nối tri thức với cuộc sống
Chọn câu trả lời đúng. Mai có thể gấp hình khai triển ở trên thành chiếc hộp nào? Hoàn thành bảng sau. Nam làm một chiếc hộp từ hình khai triển dưới đây. Việt có một chiếc hộp gỗ (có nắp) dạng hình hộp chữ nhật có chiều dài 25 cm, chiều rộng 20 cm và chiều cao 10 cm. Việt đã sơn màu nâu lên các mặt xung quanh và màu vàng lên 2 mặt đáy của chiếc hộp đó. Tính diện tích phần được sơn màu nâu.
Toán lớp 5 Bài 49. Hình khai triển của hình lập phương, hình hộp chữ nhật và hình trụ - SGK Kết nối tri thức với cuộc sống
Tìm miếng bìa là hình khai triển thích hợp với mỗi chiếc đèn lồng. Chọn câu trả lời đúng. Rô-bốt dùng miếng bìa nào dưới đây để làm chiếc đèn hình con cá? Chọn câu trả lời đúng. Hình nào dưới đây là hình khai triển của hình trụ? Chọn câu trả lời đúng. Rô-bốt có tấm bìa như hình bên. Hỏi Rô-bốt có thể gấp được hình nào dưới đây? Chọn câu trả lời đúng. Hình bên là khai triển của hình nào dưới đây?