 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài 1. Phương trình mặt phẳng - Toán 12 Chân trời sáng ..
Bài 1. Phương trình mặt phẳng - Toán 12 Chân trời sáng ..
Giải mục 5 trang 41, 42 SGK Toán 12 tập 2 - Chân trời sáng tạo
Trong không gian (Oxyz), cho mặt phẳng (left( alpha right)) có phương trình (Ax + By + Cz + D = 0) và điểm ({M_0}left( {{x_0};{y_0};{z_0}} right)). Gọi ({M_1}left( {{x_1};{y_1};{z_1}} right)) là hình chiếu vuông góc của ({M_0}) trên (left( alpha right))(hình dưới đây).
HĐ9
Trả lời câu hỏi Hoạt động 9 trang 41 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) có phương trình \(Ax + By + Cz + D = 0\) và điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\). Gọi \({M_1}\left( {{x_1};{y_1};{z_1}} \right)\) là hình chiếu vuông góc của \({M_0}\) trên \(\left( \alpha \right)\) (Hình 17).
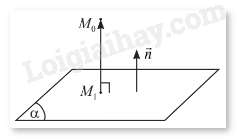
a) Nêu nhận xét về phương của hai vectơ \(\overrightarrow {{M_1}{M_0}} = \left( {{x_0} - {x_1};{y_0} - {y_1};{z_0} - {z_1}} \right)\) và \(\vec n = \left( {A;B;C} \right)\).
b) Tính \(\overrightarrow {{M_1}{M_0}} .\vec n\) theo \(A\), \(B\), \(C\), \(D\) và toạ độ của \({M_0}\).
c) Giải thích tại sao ta lại có đẳng thức \(\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|\).
d) Từ các kết quả trên suy ra cách tính \(d\left( {{M_0},\left( \alpha \right)} \right) = \left| {\overrightarrow {{M_1}{M_0}} } \right| = \frac{{\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right|}}{{\left| {\vec n} \right|}}\).
Phương pháp giải:
a) Xét vị trí tương đối của giá của hai vectơ \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\) và kết luận.
b) Sử dụng công thức tích vô hướng để tính tích \(\overrightarrow {{M_1}{M_0}} .\vec n\).
c) Sử dụng công thức nhân của hai vectơ \(\vec a.\vec b = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\) để chứng minh rằng \(\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|\).
d) Từ câu c, rút ra nhận xét.
Lời giải chi tiết:
a) Vectơ pháp tuyến \(\vec n\) có giá vuông góc với \(\left( \alpha \right)\). Do \({M_1}\) là hình chiếu của \({M_0}\) trên \(\left( \alpha \right)\) nên \({M_1}{M_0} \bot \left( \alpha \right)\), suy ra \(\overrightarrow {{M_1}{M_0}} \) có giá vuông góc với \(\left( \alpha \right)\).
Hai vectơ \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\) cùng có giá vuông góc với \(\left( \alpha \right)\), nên chúng là hai vectơ cùng phương.
b) Ta có:
\(\overrightarrow {{M_1}{M_0}} .\vec n = A\left( {{x_0} - {x_1}} \right) + B\left( {{y_0} - {y_1}} \right) + C\left( {{z_0} - {z_1}} \right) = A{x_0} + B{y_0} + C{z_0} - \left( {A{x_1} + B{y_1} + C{z_1}} \right)\)
Do \({M_1} \in \left( \alpha \right)\) nên \(A{x_1} + B{y_1} + C{z_1} + D = 0 \Rightarrow D = - \left( {A{x_1} + B{y_1} + C{z_1}} \right)\).
Như vậy \(\overrightarrow {{M_1}{M_0}} .\vec n = A{x_0} + B{y_0} + C{z_0} + D\).
c) Ta có \(\overrightarrow {{M_1}{M_0}} .\vec n = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|.\cos \left( {\overrightarrow {{M_1}{M_0}} ,\vec n} \right)\).
Do \(\overrightarrow {{M_1}{M_0}} \) và \(\vec n\) cùng phương, nên góc giữa hai vectơ này bằng \({0^o}\) (cùng chiều) hoặc \({180^o}\) (ngược chiều).
Dễ thấy rằng \(\cos {0^o} = 1\) và \(\cos {180^o} = - 1\). Suy ra \(\left| {\cos {0^o}} \right| = \left| {\cos {{180}^o}} \right| = 1\), điều này có nghĩa là \(\left| {\cos \left( {\overrightarrow {{M_1}{M_0}} ,\vec n} \right)} \right| = 1\).
Như vậy, \[\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|.\left| {\cos \left( {\overrightarrow {{M_1}{M_0}} ,\vec n} \right)} \right| = \left| {\overrightarrow {{M_1}{M_0}} } \right|.\left| {\vec n} \right|\].
d) Ta có \({M_1}{M_0} \bot \left( \alpha \right)\) và \({M_1} \in \left( \alpha \right)\) nên khoảng cách từ \({M_0}\) đến mặt phẳng \(\left( \alpha \right)\) là đoạn thẳng \({M_1}{M_0}\). Suy ra \(\left| {\overrightarrow {{M_1}{M_0}} } \right| = {M_1}{M_0} = d\left( {{M_0},\left( \alpha \right)} \right)\).
Vậy ta có \(d\left( {{M_0},\left( \alpha \right)} \right) = \left| {\overrightarrow {{M_1}{M_0}} } \right| = \frac{{\left| {\overrightarrow {{M_1}{M_0}} .\vec n} \right|}}{{\left| {\vec n} \right|}}\).
TH7
Trả lời câu hỏi Thực hành 7 trang 42 SGK Toán 12 Chân trời sáng tạo
a) Tính chiều cao của hình chóp \(O.MNP\) với toạ độ các đỉnh \(O\left( {0;0;0} \right)\), \(M\left( {2;1;2} \right)\), \(N\left( {3;3;3} \right)\), \(P\left( {4;5;6} \right)\).
b) Tính khoảng cách giữa hai mặt phẳng song song \(\left( R \right):8x + 6y + 70 = 0\) và \(\left( S \right):16x + 12y - 2 = 0\).
Phương pháp giải:
a) Chiều cao của hình chóp \(O.MNP\) chính là khoảng cách từ điểm \(O\) tới mặt phẳng \(\left( {MNP} \right)\). Viết phương trình mặt phẳng \(\left( {MNP} \right)\), từ đó tính khoảng cách từ điểm \(O\) tới mặt phẳng \(\left( {MNP} \right)\).
b) Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm nằm trên mặt phẳng này tới mặt phẳng kia. Chọn một điểm nằm trên mặt phẳng \(\left( R \right)\) và tính khoảng cách từ điểm đó tới mặt phẳng \(\left( S \right)\).
Lời giải chi tiết:
a) Chiều cao của hình chóp \(O.MNP\) chính là khoảng cách từ điểm \(O\) tới mặt phẳng \(\left( {MNP} \right)\).
Mặt phẳng \(\left( {MNP} \right)\) đi qua ba điểm \(M\left( {2;1;2} \right)\), \(N\left( {3;3;3} \right)\), \(P\left( {4;5;6} \right)\) nên có một cặp vectơ chỉ phương là \(\overrightarrow {MN} = \left( {1;2;1} \right)\) và \(\overrightarrow {MP} = \left( {2;4;4} \right)\).
Suy ra một vectơ pháp tuyến của mặt phẳng \(\left( {MNP} \right)\) là:
\(\vec n = \left[ {\overrightarrow {MN} ,\overrightarrow {MP} } \right] = \left( {2.4 - 1.4;1.2 - 1.4;1.4 - 2.2} \right) = \left( {4; - 2;0} \right)\)
Mặt phẳng \(\left( {MNP} \right)\) đi qua \(M\left( {2;1;2} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {4; - 2;0} \right)\) nên có phương trình là \(4\left( {x - 2} \right) - 2\left( {y - 1} \right) + 0\left( {z - 2} \right) = 0 \Leftrightarrow 4x - 2y - 6 = 0\).
Khoảng cách từ điểm \(O\) tới mặt phẳng \(\left( {MNP} \right)\) là:
\(d\left( {O,\left( {MNP} \right)} \right) = \frac{{\left| {4.0 - 2.0 - 6} \right|}}{{\sqrt {{4^2} + {{\left( { - 2} \right)}^2}} }} = \frac{6}{{2\sqrt 5 }} = \frac{{3\sqrt 5 }}{5}\).
b) Chọn điểm \(M\left( {0; - \frac{{35}}{3};0} \right)\) nằm trên mặt phẳng \(\left( R \right)\).
Khoảng cách giữa hai mặt phẳng song song \(\left( R \right)\) và \(\left( S \right)\), chính là khoảng cách từ \(M\left( {0; - \frac{{35}}{3};0} \right)\) đến \(\left( S \right)\), bằng:
\(d\left( {\left( R \right),\left( S \right)} \right) = d\left( {M,\left( S \right)} \right) = \frac{{\left| {16.0 + 12.\frac{{ - 35}}{3} - 2} \right|}}{{\sqrt {{{16}^2} + {{12}^2}} }} = \frac{{71}}{{10}}\).
VD6
Trả lời câu hỏi Vận dụng 6 trang 42 SGK Toán 12 Chân trời sáng tạo
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 2 \), chiều cao bằng \(2a\) và \(O\) là tâm của đáy. Bằng cách thiết lập hệ trục toạ độ \(Oxyz\) như hình dưới đây, tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
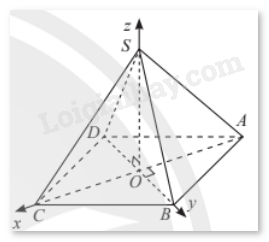
Phương pháp giải:
Xác định toạ độ các điểm \(C\), \(S\), \(A\), \(B\), sau đó viết phương trình mặt phẳng \(\left( {SAB} \right)\) rồi sử dụng công thức tính khoảng cách để tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {SAB} \right)\).
Lời giải chi tiết:
Hình vuông \(ABCD\) có cạnh \(a\sqrt 2 \), nên đường chéo có độ dài \(\sqrt {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = 2a\). Suy ra \(OA = OB = OC = \frac{{2a}}{2} = a\).
Chiều cao của hình chóp đều là \(2a\), nên \(SO = 2a\)
Điểm \(A\) nằm trên trục \(Ox\), \(OA = a\) và \({x_A} < 0\) nên ta có \(A\left( { - a;0;0} \right)\).
Điểm \(B\) nằm trên trục \(Oy\), \(OB = a\) và \({y_B} > 0\) nên ta có \(B\left( {0;a;0} \right)\).
Điểm \(C\) nằm trên trục \(Ox\), \(OC = a\) và \({x_C} > 0\) nên ta có \(C\left( {a;0;0} \right)\).
Điểm \(S\) nằm trên trục \(Oz\), \(OS = 2a\) và \({z_S} > 0\) nên ta có \(S\left( {0;0;2a} \right)\).
Mặt phẳng \(\left( {SAB} \right)\) đi qua \(A\left( { - a;0;0} \right)\), \(B\left( {0;a;0} \right)\), \(S\left( {0;0;2a} \right)\) nên có phương trình là:
\(\frac{x}{{ - a}} + \frac{y}{a} + \frac{z}{{2a}} = 1 \Leftrightarrow - 2x + 2y + z = 2a \)
\(\Leftrightarrow - 2x + 2y + z - 2a = 0\).
Khoảng cách từ \(C\left( {a;0;0} \right)\) đến mặt phẳng \(\left( {SAB} \right)\) là:
\(d\left( {C,\left( {SAB} \right)} \right) = \frac{{\left| { - 2.a + 2.0 + 0 - 2a} \right|}}{{\sqrt {{{\left( { - 2} \right)}^2} + {2^2} + {1^2}} }} = \frac{{4a}}{3}\).
- Giải bài tập 1 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 2 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 3 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 4 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 5 trang 42 SGK Toán 12 tập 2 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận