Bài 2. Tiếp tuyến của đường tròn - Toán 9 Chân trời sán..

Giải mục 3 trang 87, 88 SGK Toán 9 tập 1 - Chân trời sáng tạo

Cho đường tròn O và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10). a) Chứng minh hai tam giác ABO và ACO bằng nhau. b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.

Lựa chọn câu để xem lời giải nhanh hơn

HĐ3

Video hướng dẫn giải

Trả lời câu hỏi Hoạt động 3 trang 87 SGK Toán 9 Chân trời sáng tạo

Cho đường tròn O và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).

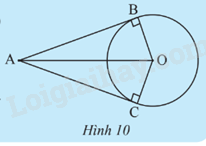
a) Chứng minh hai tam giác ABO và ACO bằng nhau.

b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.

Phương pháp giải:

- Dựa vào chứng minh 2 tam giác bằng nhau theo cạnh huyền - cạnh góc vuông.

- Vì 2 tam giác bằng nhau nên các góc và các cạnh trong tam giác bằng nhau.

Lời giải chi tiết:

a) Xét tam giác ABO và ACO có:

\(\widehat {ABO} = \widehat {ACO} = {90^o}\)

AO chung

OB = OC = R

Suy ra \(\Delta \)ABO = \(\Delta \)ACO (cạnh huyền - cạnh góc vuông)

b) Theo Hình 10, ta có: \(\Delta \)ABO = \(\Delta \)ACO

suy ra AB = AC; BO = CO

\(\begin{array}{l}\widehat {ABO} = \widehat {ACO} = {90^o}\\\widehat {BAO} = \widehat {CAO}\\\widehat {AOB} = \widehat {AOC}\end{array}\)

TH3

Video hướng dẫn giải

Trả lời câu hỏi Thực hành 3 trang 87 SGK Toán 9 Chân trời sáng tạo

Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết \(\widehat {EMF} = {60^o}\).

a) Tính số đo \(\widehat {EMI}\) và \(\widehat {EIF}\) .

b) Tính độ dài MI.

Phương pháp giải:

- Dựa vào dữ kiện đề bài để vẽ hình.

- Dựa vào định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại 1 điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến để tính \(\widehat {EMI}\). Tính \(\widehat {EIF}\) dựa vào tính chất trong một tứ giác tổng các góc bằng 360^o.

- Tính MI áp dụng tỉ số lượng giác trong tam giác vuông MIE: Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin.

Lời giải chi tiết:

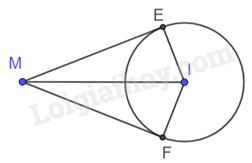
a) Ta có hai tiếp tuyến ME và MF cắt nhau tại M nên MI là tia phân giác \(\widehat {EMF}\).

Suy ra \(\widehat {EMI} = \frac{{\widehat {EMF}}}{2} = \frac{{{{60}^o}}}{2} = {30^o}\).

Xét tứ giác MEFI ta có

\(\begin{array}{l}\widehat {EIF} = {360^o} - (\widehat {EMF} + \widehat {MFI} + \widehat {MEI})\\ = {360^o} - (\widehat {EMF} + 2\widehat {MFI})\\ = {360^o} - ({60^o} + {2.90^o})\\ = {120^o}\end{array}\)

b) Xét tam giác MEI vuông tại E, MI = 6 cm; \(\widehat {EMI} = {30^o}\) ta có

sin \(\widehat {EMI}\) = \(\frac{{EI}}{{MI}}\) suy ra MI = \(\frac{{EI}}{{\sin \widehat {EMI}}} = \frac{6}{{\sin {{30}^o}}} = 12\)cm.

TH4

Video hướng dẫn giải

Trả lời câu hỏi Thực hành 4 trang 88 SGK Toán 9 Chân trời sáng tạo

Tìm giá trị x trong Hình 12.

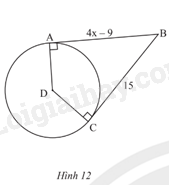
Phương pháp giải:

Chứng minh BA và BC là tiếp tuyến cùa đường tròn (D; DA).

Suy ra AB = BC để tìm x.

Lời giải chi tiết:

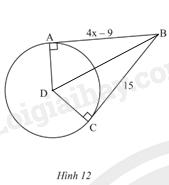
Nối B với D.

Vì BA \(\bot\) DA tại A; BC \(\bot\) DC tại C nên BA và BC là hai tiếp tuyến của đường tròn (D; DA).

Hai tiếp tuyến BA và BC cắt nhau tại B nên BA = BC.

hay 4x – 9 = 15 suy ra x = 6.

VD3

Video hướng dẫn giải

Trả lời câu hỏi Vận dụng 3 trang 88 SGK Toán 9 Chân trời sáng tạo

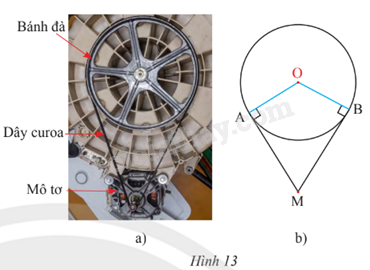
Bánh đà của một động cơ được thiết kế có dạng một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình 13). Cho biết khoảng cách OM là 35 cm.

a) Tính độ dài của hai đoạn dây curoa MA và MB (kết quả làm tròn đến hàng phần mười).

b) Tính số đo \(\widehat {AMB}\) tạo bởi hai tiếp tuyến AM, BM và số đo \(\widehat {AOB}\) (kết quả làm tròn đến phút).

Phương pháp giải:

- Áp dụng định lý Pythagore vào tam giác AOM vuông tại A để tính MA suy ra MB.

- Áp dụng tỉ số lượng giác trong tam giác vuông AMO: Tỉ số giữa cạnh đối và cạnh kề được gọi là tan. Sau đó dùng máy tính bấm ra góc \(\widehat {AMO}\) suy ra góc \(\widehat {AMB}\). Tính \(\widehat {AOB}\) bằng cách dựa vào tính chất trong một tứ giác tổng các góc bằng 360^o.

Lời giải chi tiết:

a) Áp dụng định lý Pythagore vào tam giác AOM vuông tại A, ta có:

MA = \(\sqrt {O{M^2} - O{A^2}} = \sqrt {{{35}^2} - {{15}^2}} = 31,6cm\)

MA và MB là hai tiếp tuyến của (O; 15cm) cắt nhau tại M nên MA = MB = 31,6 cm.

b) Ta có \(\widehat {AMB}\) tạo bởi hai tiếp tuyến AM, BM có MO là phân giác nên \(\widehat {AMB}\) = 2\(\widehat {AMO}\).

Xét tam giác AOM vuông tại A, ta có:

sin \(\widehat {AMO}\) = \(\frac{{AO}}{{MO}} = \frac{{15}}{{35}} = \frac{3}{7}\)

suy ra \(\widehat {AMO} \approx {25^o}23'\) nên \(\widehat {AMB}\)= 2\(\widehat {AMO} \approx {50^o}46'\)

\(\begin{array}{l}\widehat {AOB} = {360^o} - (2\widehat {AOM} + \widehat {AMB})\\ = {360^o} - ({2.90^o} + {50^o}46')\\ = {129^o}14'\end{array}\)

Bình luận

Chia sẻ

Bình chọn:

4 trên 3 phiếu

Bài tiếp theo

Giải bài tập 1 trang 88 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trong Hình 14, MB, MC lần lượt là tiếp tuyến của đường tròn (O) tại B, C; (widehat {COB} = {130^o}). Tính số đo (widehat {CMB}) .
Giải bài tập 2 trang 88 SGK Toán 9 tập 1 - Chân trời sáng tạo
Quan sát Hình 15. Biết AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C. Tính giá trị của x.
Giải bài tập 3 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trong Hình 16, AB = 9; BC = 12; AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).
Giải bài tập 4 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho tam giác ABC có đương tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm; BP = 3 cm; CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.
Giải bài tập 5 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng: a) (widehat {ACB}) có số đo bằng 90o, từ đó suy ra độ dài của BC theo R; b) OM là tia phân giác của (widehat {COA}). c) MC là tiếp tuyến của đường tròn (O; R).
Giải bài tập 6 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho đường tròn (O; 5 cm) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) vuông góc với nhau tại M. a) Tính độ dài MA và MB. b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài CD.
Giải bài tập 7 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho đường tròn (O) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) thoả mãn (widehat {AMB} = {60^o}). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.
Giải bài tập 8 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B. a) Tính bán kính r của đường tròn (O). b) Tính chiều dài cạnh OA của tam giác ABO.
Giải mục 2 trang 85, 86 SGK Toán 9 tập 1 - Chân trời sáng tạo
Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A). a) Giải thích tại sao ta có OA = R và OM > R. b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.
Giải mục 1 trang 83, 84, 85 SGK Toán 9 tập 1 - Chân trời sáng tạo
Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn (O) trong mỗi hình sau:
Lý thuyết Tiếp tuyến của đường tròn Toán 9 Chân trời sáng tạo
1. Vị trí tương đối của đường thẳng và đường tròn Đường thẳng a và đường tròn (O) có duy nhất một điểm chung C thì ta nói a tiếp xúc với (O) tại C, khi đó a là tiếp tuyến của đường tròn (O) tại C và C là tiếp điểm.