Lý thuyết Hình cầu Toán 9 Chân trời sáng tạo

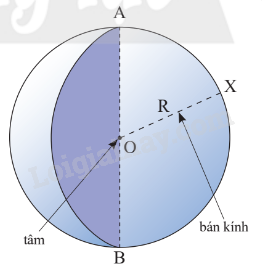
1. Hình cầu Định nghĩa Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định ta được một hình cầu tâm O, bán kính R. Khi đó, nửa đường tròn quét thành một mặt cầu. Ta cũng gọi O và R lần lượt là tâm và bán kính của mặt cầu đó. Đoạn thẳng đi qua tâm của hình cầu với hai đầu mút nằm trên mặt cầu gọi là đường kính của hình cầu (hay mặt cầu).

1. Hình cầu

Định nghĩa

Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định ta được một hình cầu tâm O, bán kính R.

Khi đó, nửa đường tròn quét thành một mặt cầu. Ta cũng gọi O và R lần lượt là tâm và bán kính của mặt cầu đó.

Đoạn thẳng đi qua tâm của hình cầu với hai đầu mút nằm trên mặt cầu gọi là đường kính của hình cầu (hay mặt cầu).

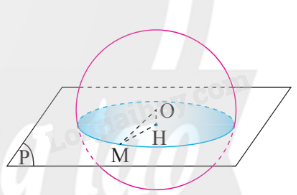
Phần chung của mặt phẳng và mặt cầu

Khi cắt hình cầu bởi một mặt phẳng thì phần chung của mặt cầu và mặt phẳng (còn gọi là mặt cắt) là một hình tròn.

2. Diện tích của mặt cầu

Diện tích S của mặt cầu có bán kính R là:

\(S = 4\pi {R^2}\).

Ví dụ:

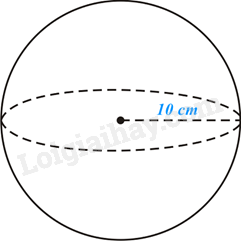
Diện tích mặt cầu là:

\(S = 4\pi {R^2} = 4\pi {.10^2} = 400\pi \left( {c{m^2}} \right)\),

3. Thể tích hình cầu

Thể tích của hình cầu có bán kính R là

\(V = \frac{4}{3}\pi {R^3}\).

Ví dụ:

Thể tích hình cầu là:

\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.10^3} = \frac{{4000\pi }}{3}\left( {c{m^3}} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 93, 94, 95 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cho tấm bìa có dạng nửa hình tròn tâm O và đường kính AB cố định (Hình 1a). Quay tấm bìa quanh đường kính AB thì hình tạo ra giống với vật thể quen thuộc nào?
Giải mục 2 trang 95, 96 SGK Toán 9 tập 2 - Chân trời sáng tạo
Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R. a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b. b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
Giải mục 3 trang 96 SGK Toán 9 tập 2 - Chân trời sáng tạo
Một quả cầu có bán kính R nằm khít trong chiếc bình hình trụ đổ đầy nước có chiều cao h = 2R (Hình 12a). Rút qua cầu ra khỏi bình nước, ta thấy chiều cao của mực nước bằng \(\frac{1}{3}\) chiều cao h (Hình 12b). Hãy tính theo R: a) Thể tích của chiếc bình hình trụ; b) Thể tích của nước ở trong bình; c) Thể tích của hình cầu.
Giải bài tập 1 trang 96 SGK Toán 9 tập 2 - Chân trời sáng tạo
Đồ vật nào sau đây có dạng hình cầu?
Giải bài tập 2 trang 97 SGK Toán 9 tập 2 - Chân trời sáng tạo
Quan sát hình cầu ở Hình 16. Hãy cho biết tâm, bán kính, diện tích mặt cầu và thể tích của hình cầu đó.
Giải bài tập 3 trang 97 SGK Toán 9 tập 2 - Chân trời sáng tạo
Bể cá ở Hình 17 là một phần của một hình cầu. Hỏi mặt nước trong bể cá có dạng hình gì?
Giải bài tập 4 trang 97 SGK Toán 9 tập 2 - Chân trời sáng tạo
Cắt một hình cầu có bán kính 5 cm bằng một mặt phẳng đi qua tâm ta sẽ được hai nửa hình cầu. Nam cầu sơn tất cả các mặt của một nửa hình cầu này (Hình 18). Hỏi diện tích Nam cần sơn là bao nhiêu (kết quả làm tròn đến hàng đơn vị)?
Giải bài tập 5 trang 97 SGK Toán 9 tập 2 - Chân trời sáng tạo
Phần bên trong của một cái li có dạng hình nón có bán kính đáy 2 cm, độ dài đường sinh 8 cm. Người ta đựng đầy kem trong li và thêm một nửa hình cầu kem phía trên (Hình 19). Tính thể tích của kem (kết quả làm tròn đến hàng đơn vị).