 Giải khoa học tự nhiên 8, soạn sgk khtn lớp 8 chân trời sáng tạo
Giải khoa học tự nhiên 8, soạn sgk khtn lớp 8 chân trời sáng tạo
 Chủ đề 3. Khối lượng riêng, áp suất và moment lực - KHT..
Chủ đề 3. Khối lượng riêng, áp suất và moment lực - KHT.. Bài 15. Khối lượng riêng trang 77, 78, 79 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
Làm thế nào để xác định khối lượng nước chứa đầy trong một bồn đặt ở trên cao?
Câu hỏi tr 77 CHMĐ
Trả lời câu hỏi mở đầu trang 77 SGK KHTN 8 Chân trời sáng tạo
Làm thế nào để xác định khối lượng nước chứa đầy trong một bồn đặt ở trên cao?

Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
Để xác định khối lượng nước chứa đầy trong một bồn đặt ở trên cao ta sử dụng công thức tính khối lượng: m = D.V.
Với D là khối lượng riêng của nước (kg/m3), V là thể tích nước chứa trong bồn (m3).
Câu hỏi tr 77 CH
Trả lời câu hỏi trang 77 SGK KHTN 8 Chân trời sáng tạo
1. Trong hai phương án ở bên, phương án nào là thuận tiện nhất. Vì sao?
2. Biết rằng 1 L nước có khối lượng bằng 1 kg, hãy trả lời câu hỏi đã nên ở phân Mở đầu bài học.
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
1. Phương án thứ hai: Biết khối lượng của một thể tích nước xác định rồi suy ra khối lượng nước toàn bình là thuận tiện nhất.
Vì ta dễ dàng thực hiện phép đo khối lượng của một thể tích nước xác định hơn là thực hiện phép đo khối lượng cho toàn bộ lượng nước chứa trong bồn.
2. 1 L nước có khối lượng 1 kg nên 500 L nước có khối lượng 500 kg.
Vậy để xác định khối lượng nước trong bồn đặt ở trên cao ta cần biết khối lượng của một đơn vị thể tích nước đó rồi suy ra khối lượng nước toàn bình khi đã biết thể tích nước chứa trong bình.
Câu hỏi tr 78 CH
Trả lời câu hỏi trang 78 SGK KHTN 8 Chân trời sáng tạo
Nói khối lượng riêng của đồng là 8 900 kg/m3 có nghĩa là gì? Đổi khối lượng riêng này ra đơn vị g/cm3.
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
- Nói khối lượng riêng của đồng là 8 900 kg/m3 có nghĩa là khối lượng của 1 m3 của chất đồng là 8 900 kg.
\(8900kg/{m^3} = \frac{{{{8900.10}^3}}}{{{{10}^6}}} = 8,9g/c{m^3}\)
Câu hỏi tr 78 LT 1
Trả lời câu hỏi luyện tập 1 trang 78 SGK KHTN 8 Chân trời sáng tạo
Cho biết 2 m3 sắt có khối lượng là 15 600 kg. Tính khối lượng riêng của sắt.
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
Khối lượng riêng của sắt là \(D = \frac{m}{V} = \frac{{15600}}{2} = 7800kg/{m^3}\)
Câu hỏi tr 78 TN
Trả lời câu hỏi thí nghiệm trang 78 SGK KHTN 8 Chân trời sáng tạo
Thí nghiệm xác định khối lượng riêng của khối hộp chữ nhật
Chuẩn bị: một vật rắn đặc có dạng khối hộp chữ nhật (khối gỗ, khối kim loại, cục tẩy, …), thước kẻ, cân điện tử.
Tiến hành thí nghiệm:
Bước 1: Đo khối lượng m của khối hộp chữ nhật (Hình 15.1 a).
Bước 2: Đo chiều dài a, chiều rộng b và chiều cao c của khối hộp chữ nhật (Hình 15.1 b). Tính thể tích của khối hộp chữ nhật V = a x b x c.
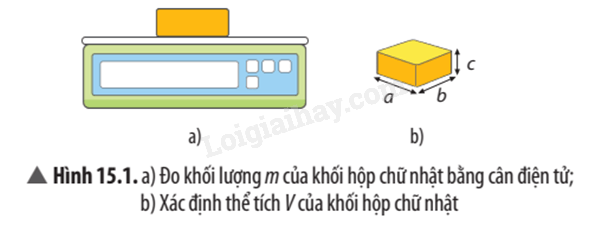
Bước 3: Thực hiện đo ba lần. Ghi kết quả theo mẫu Bảng 15.2. Tính giá trị trung bình của các phép đo.

Bước 4: Dùng công thức \(D = \frac{m}{V}\) để tính khối lượng riêng của khối hộp.
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
Giả sử, ta thực hiện thí nghiệm với khối hộp chữ nhật bằng gỗ. Làm theo các bước ta thu được bảng 15.2 như sau:
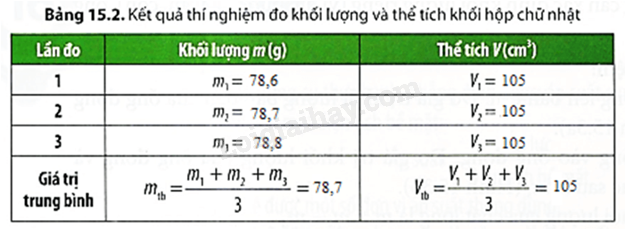
Khối lượng riêng của khối hộp gỗ hình chữ nhật là
\(D = \frac{m}{V} = \frac{{78,7}}{{105}} \approx 0,75g/c{m^3}\)
Câu hỏi tr 78 LT 2
Trả lời câu hỏi luyện tập 2 trang 78 SGK KHTN 8 Chân trời sáng tạo
Hãy xác định khối lượng riêng của vật có dạng khối lập phương trong hình dưới đây.
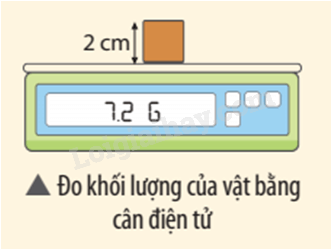
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
Thể tích của vật là \(V = {2^3} = 8c{m^3}\)
Khối lượng riêng của vật là \(D = \frac{m}{V} = \frac{{7,2}}{8} = 0,9g/c{m^3}\)
Câu hỏi tr 79 TN
Trả lời câu hỏi thí nghiệm trang 79 SGK KHTN 8 Chân trời sáng tạo
Thí nghiệm xác định khối lượng riêng của vật rắn có hình dạng bất kì
Chuẩn bị: một vật rắn đặc có hình dạng bất kì bỏ lọt ống đong và không thấm nước (hòn sỏi, viên đá, …), ống đong, cân điện tử.
Tiến hành thí nghiệm:
Bước 1: Đo khối lượng m của vật (Hình 15.2 a).
Bước 2: Rót nước vào ống đong, thể tích nước đo được ban đầu là Vđ. Sau đó, thả vật vào ống đong, thể tích nước và vật rắn đo được là Vs (Hình 15.2 b).
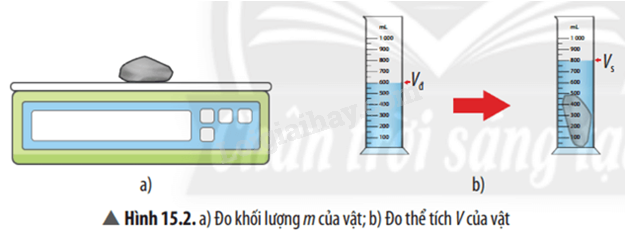
Thể tích của nước dâng lên, đồng thời cũng là thể tích của vật:
V = Vs – Vđ
Bước 3: Thực hiện đo ba lần. Ghi kết quả theo mẫu Bảng 15.3. Tính giá trị trung bình của các phép đo.
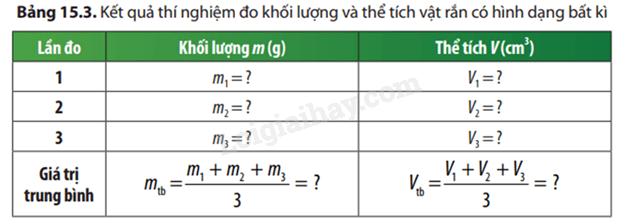
Bước 4: Tính khối lượng riêng D của vật rắn.
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
Giả sử, ta thực hiện thí nghiệm với một hòn sỏi. Làm theo các bước ta thu được bảng 15.3 như sau:
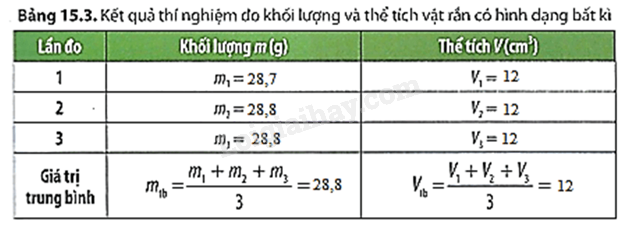
Khối lượng riêng của hòn sỏi là \(D = \frac{m}{V} = \frac{{28,8}}{{12}} \approx 2,4g/c{m^3}\)
Câu hỏi tr 79 CH
Trả lời câu hỏi trang 79 SGK KHTN 8 Chân trời sáng tạo
Với thí nghiệm Hình 15.2, ta có thể xác định khối lượng riêng của những vật nào thường gặp trong cuộc sống hằng ngày?
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
Với thí nghiệm Hình 15.2, ta có thể xác định khối lượng riêng của những vật thường gặp trong cuộc sống hằng ngày như: ổ khóa, chìa khóa, ly rượu nhỏ, chén trà nhỏ, …..
Câu hỏi tr 79 VD
Trả lời câu hỏi vận dụng trang 79 SGK KHTN 8 Chân trời sáng tạo
Cho một thanh sắt và một ống sắt hình trụ tròn, có cùng chiều dài và đường kính ngoài (hình dưới). Hãy trình bày cách xác định khối lượng riêng của từng vật.

Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
- Xác định khối lượng riêng của thanh sắt:
+ Bước 1: Dùng cân đo khối lượng m của thanh sắt.
+ Bước 2: Đo chiều dài của thanh sắt h (cm), đường kính hình tròn mặt đáy của thanh sắt d (cm).
Thể tích của thanh sắt là \(V = \pi .{\left( {\frac{d}{2}} \right)^2}.h\)
+ Bước 3: Dùng công thức \(D = \frac{m}{V}\left( {g/c{m^3}} \right)\) để tính khối lượng riêng của thanh sắt.
- Xác định khối lượng riêng của ống sắt:
+ Bước 1: Dùng cân đo khối lượng m của ống sắt.
+ Bước 2: Đo chiều dài của ống sắt h (cm), đường kính ngoài và đường kính trong hình tròn mặt đáy của ống sắt lần lượt là d1 (cm) và d2 (cm)
Thể tích của ống sắt là \(V = \pi .h.\left( {{{\left( {\frac{{{d_1}}}{2}} \right)}^2} - {{\left( {\frac{{{d_2}}}{2}} \right)}^2}} \right)\)
+ Bước 3: Dùng công thức \(D = \frac{m}{V}\left( {g/c{m^3}} \right)\) để tính khối lượng riêng của ống sắt.
Câu hỏi tr 80 TN
Trả lời câu hỏi thí nghiệm trang 80 SGK KHTN 8 Chân trời sáng tạo
Thí nghiệm xác định khối lượng riêng của chất lỏng
Chuẩn bị: chất lỏng cần xác định khối lượng riêng (ví dụ: nước, dầu ăn, cồn), ống đong, cân điện tử.
Tiến hành thí nghiệm:
Bước 1: Đặt ống đong lên bàn cân. Đo giá trị khối lượng ban đầu của ống đong là mđ (Hình 15.3a).
Bước 2: Rót chất lỏng vào ống đong. Đo giá trị khối lượng của ống đong và chất lỏng lúc sau là ms (Hình 15.3b).
Từ đó, tính được khối lượng của chất lỏng là m = ms – mđ.
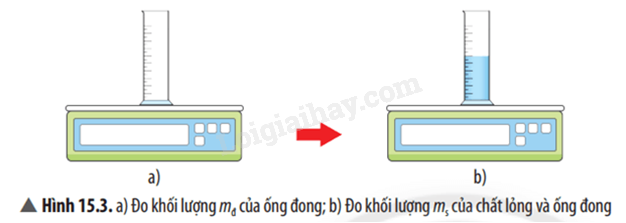
Bước 3: Đo thể tích V của chất lỏng.
Bước 4: Thực hiện đo ba lần với cùng một lượng chất lỏng. Ghi kết quả theo mẫu Bảng 15.4. Tính giá trị trung bình của các phép đo.

Bước 5: Tính khối lượng riêng D của chất lỏng.
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
Giả sử, ta thực hành thí nghiệm với chất lỏng là nước. Làm các bước theo hướng dẫn ta thu được bảng 15.4 như sau:

Khối lượng riêng của nước là \(D = \frac{m}{V} = \frac{{98}}{{100}} = 0,98g/mL\)
Câu hỏi tr 80 VD
Trả lời câu hỏi vận dụng trang 80 SGK KHTN 8 Chân trời sáng tạo
Bồn chứa của một chiếc xe chở xăng có thể tích 26 m3. Tính khối lượng xăng tối đa có thể chứa trong bồn, biết khối lượng riêng của xăng là 750 kg/m3.
Phương pháp giải:
Vận dụng lí thuyết về khối lượng riêng và công thức tính khối lượng riêng \(D = \frac{m}{V}\)
Lời giải chi tiết:
Khối lượng xăng tối đa có thể chứa trong bồn là
m = D. V = 750 . 26 = 19 500 kg
- Bài 16. Áp suất trang 81, 82, 83 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 17. Áp suất trong chất lỏng trang 84, 85, 86 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 18. Áp suất trong chất khí trang 89, 90, 91 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 19. Tác dụng làm quay của lực – Moment lực trang 92, 93, 94 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 20. Đòn bẩy trang 95, 96, 97 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
>> Xem thêm
Các bài khác cùng chuyên mục
- Ôn tập chủ đề 5 trang 133 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 28. Sự nở vì nhiệt trang 128, 129, 130 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 27. Sự truyền nhiệt trang 123, 124, 125 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 26. Năng lượng nhiệt và nội năng trang 120, 121, 122 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Ôn tập chủ đề 4 trang 119 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Ôn tập chủ đề 5 trang 133 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 28. Sự nở vì nhiệt trang 128, 129, 130 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 27. Sự truyền nhiệt trang 123, 124, 125 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Bài 26. Năng lượng nhiệt và nội năng trang 120, 121, 122 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo
- Ôn tập chủ đề 4 trang 119 SGK Khoa học tự nhiên 8 - Chân trời sáng tạo












Danh sách bình luận