Giải bài tập 7.27 trang 40 SGK Toán 9 tập 2 - Cùng khám phá
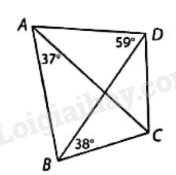
Cho ABCD là tứ giác nội tiếp có \(\widehat {BAC} = {37^o},\widehat {ADB} = {59^o}\) và \(\widehat {CBD} = {38^o}\). Số đo của góc ADC bằng A. 75\(^o\) B. 96\(^o\) C. 97\(^o\) D. 87\(^o\)
Đề bài
Cho ABCD là tứ giác nội tiếp có \(\widehat {BAC} = {37^o},\widehat {ADB} = {59^o}\) và \(\widehat {CBD} = {38^o}\). Số đo của góc ADC bằng
A. 75\(^o\)
B. 96\(^o\)
C. 97\(^o\)
D. 87\(^o\)
Phương pháp giải - Xem chi tiết
Trong một tứ giác nội tiếp tổng hai góc đối bằng 180\(^o\)
Lời giải chi tiết
Ta có: \(\widehat {BDC} = \widehat {BAC} = {37^o}\) (hai góc nội tiếp cùng chắn cung BC)
Suy ra \(\widehat {ADC} = \widehat {ADB} + \widehat {BDC} = {59^o} + {37^o} = {96^o}\)
Chọn đáp án B.
- Giải bài tập 7.28 trang 40 SGK Toán 9 tập 2 - Cùng khám phá
- Giải bài tập 7.26 trang 40 SGK Toán 9 tập 2 - Cùng khám phá
- Giải bài tập 7.25 trang 40 SGK Toán 9 tập 2 - Cùng khám phá
- Giải bài tập 7.24 trang 40 SGK Toán 9 tập 2 - Cùng khám phá
- Giải bài tập 7.23 trang 40 SGK Toán 9 tập 2 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá













Danh sách bình luận