 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 1. Phương trình mặt phẳng - Toán 12 Cùng khám phá
Bài 1. Phương trình mặt phẳng - Toán 12 Cùng khám phá
Giải bài tập 5.14 trang 53 SGK Toán 12 tập 2 - Cùng khám phá
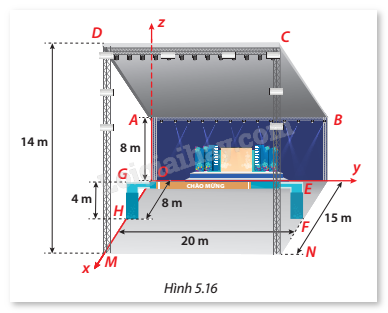
Người ta thiết kế một mái che hình chữ nhật ABCD phía trên sân khấu. a) Với hệ trục Oxyz (đơn vị trên trục là mét) và các kích thước được cho như Hình 5.16, hãy viết phương trình mặt phẳng chứa mái che. b) Một cổng chào hình chữ nhật EFHG cao 4 m dựng vuông góc với mặt đất. Người ta muốn làm các đoạn dây nối thanh ngang GE với mái che để gắn hoa và đèn led. Tính độ dài ngắn nhất của mỗi đoạn dây này.
Đề bài
Người ta thiết kế một mái che hình chữ nhật ABCD phía trên sân khấu.
a) Với hệ trục Oxyz (đơn vị trên trục là mét) và các kích thước được cho như Hình 5.16, hãy viết phương trình mặt phẳng chứa mái che.
b) Một cổng chào hình chữ nhật EFHG cao 4 m dựng vuông góc với mặt đất. Người ta muốn làm các đoạn dây nối thanh ngang GE với mái che để gắn hoa và đèn led. Tính độ dài ngắn nhất của mỗi đoạn dây này.
Phương pháp giải - Xem chi tiết
a) Xác định tọa độ các điểm A, B, C, D của mái che. Sử dụng 3 điểm để viết phương trình mặt phẳng chứa mái che. Tìm hai vectơ chỉ phương và tính tích có hướng để xác định vectơ pháp tuyến của mặt phẳng. Dùng vectơ pháp tuyến viết phương trình mặt phẳng.
b) Tìm tọa độ các điểm G, E. Tính khoảng cách từ điểm G hoặc E đến mặt phẳng chứa mái che. Sử dụng công thức khoảng cách từ một điểm đến mặt phẳng để tính độ dài ngắn nhất của đoạn dây.
Lời giải chi tiết
a)
Giả sử tọa độ các điểm của mái che là:
\(A(0;0;8),\quad B(0;20;8),\quad C(15;20;14),\quad D(15;0;14).\)
Các điểm này nằm trên mặt phẳng chứa mái che. Tính hai vectơ chỉ phương:
\(\overrightarrow {AB} = (0;20;0),\quad \overrightarrow {AC} = (15;20;6).\)
Tích có hướng của hai vectơ:
\(\vec n = \overrightarrow {AB} \times \overrightarrow {AC} = (120;0; - 300).\)
Vectơ pháp tuyến của mặt phẳng là \(\vec n = (120;0; - 300)\). Phương trình mặt phẳng có dạng:
\(120(x - 0) + 0y - 300(z - 8) = 0\quad \Rightarrow \quad 120x - 300z + 2400 = 0\,\,\, \Leftrightarrow \,\,\,2x - 5z + 40 = 0\)
Vậy phương trình mặt phẳng chứa mái che là \(\,2x - 5z + 40 = 0\).
b)
Giả sử tọa độ các điểm \(G(0;0;4)\).
Khoảng cách từ điểm \(G(0;0;4)\) đến mặt phẳng \((ABCD)\) chính là độ dài ngắn nhất của đoạn dây nối từ thanh ngang GE với mái che được tính bằng công thức:
\(d = \frac{{|2.0 - 5.4 + 40|}}{{\sqrt {{2^2} + {{( - 5)}^2}} }} = \frac{{20}}{{\sqrt {29} }}\)
Vậy độ dài ngắn nhất của mỗi đoạn dây là \(\frac{{20}}{{\sqrt {29} }}\) mét.
- Giải bài tập 5.13 trang 52 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.12 trang 52 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.11 trang 52 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.10 trang 52 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.9 trang 52 SGK Toán 12 tập 2 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận