 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài 1. Xác suất có điều kiện - Toán 12 Chân trời sáng tạo
Bài 1. Xác suất có điều kiện - Toán 12 Chân trời sáng tạo
Giải bài tập 3 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
Mỗi bạn học sinh trong lớp của Minh lựa chọn học một trong hai ngoại ngữ là tiếng Anh hoặc tiếng Nhật. Xác suất chọn tiếng Anh của mỗi bạn học sinh nữ là 0,6 và của mỗi bạn học sinh nam là 0,7. Lớp của Minh có 25 bạn nữ và 20 bạn nam. Chọn ra ngẫu nhiên một bạn trong lớp. Sử dụng sơ đồ hình cây, tính xác suất của các biến cố: (A): “Bạn được chọn là nam và học tiếng Nhật” (B): “Bạn được chọn là nữ và học tiếng Anh”
Đề bài
Mỗi bạn học sinh trong lớp của Minh lựa chọn học một trong hai ngoại ngữ là tiếng Anh hoặc tiếng Nhật. Xác suất chọn tiếng Anh của mỗi bạn học sinh nữ là 0,6 và của mỗi bạn học sinh nam là 0,7. Lớp của Minh có 25 bạn nữ và 20 bạn nam. Chọn ra ngẫu nhiên một bạn trong lớp.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(A\): “Bạn được chọn là nam và học tiếng Nhật”.
\(B\): “Bạn được chọn là nữ và học tiếng Anh”.
Phương pháp giải - Xem chi tiết
Gọi \(M\) là biến cố “Bạn được chọn là nam”, \(N\) là biến cố “Bạn được chọn học tiếng Anh”. Sử dụng sơ đồ hình cây, từ đó tính được \(P\left( A \right)\) và \(P\left( B \right)\).
Lời giải chi tiết
Gọi \(M\) là biến cố “Bạn được chọn là nam”, \(N\) là biến cố “Bạn được chọn học tiếng Anh”. Lớp có 25 bạn nữ và 20 bạn nam nên xác suất chọn được 1 bạn nam là \(P\left( M \right) = \frac{{20}}{{45}} = \frac{4}{9}\). Từ đó, ta có sơ đồ hình cây sau:
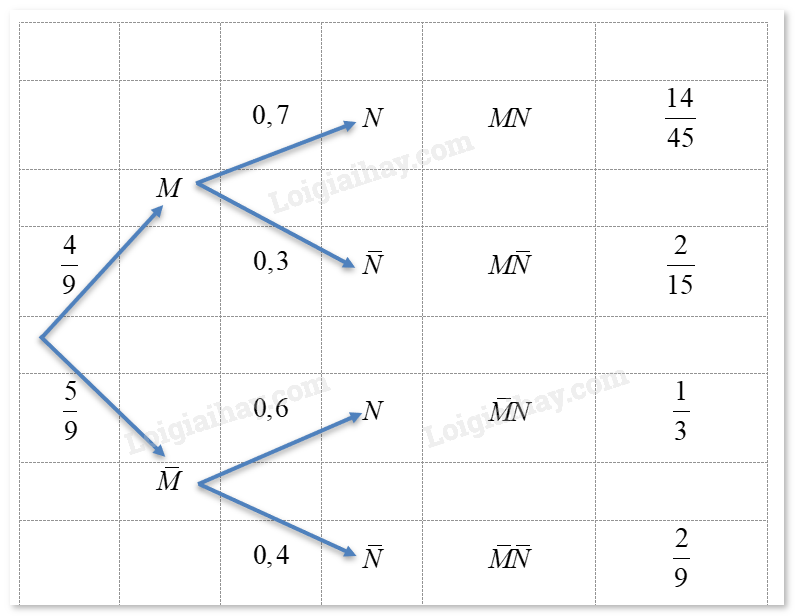
Từ sơ đồ hình cây, suy ra:
\(P\left( A \right) = P\left( {M\bar N} \right) = \frac{2}{{15}}\) và \(P\left( B \right) = P\left( {\bar MN} \right) = \frac{1}{3}.\)
- Giải bài tập 4 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 2 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 1 trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải mục 3 trang 72, 73, 74 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải mục 2 trang 70, 71, 72 SGK Toán 12 tập 2 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận