SBT Toán 11 - giải SBT Toán 11 - Kết nối tri thức với cuộc sống Bài tập cuối chương VII - SBT Toán 11 KNTT

Giải bài 7.49 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống


Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Thể tích khối tứ diện ABC’D’ bằng

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Thể tích khối tứ diện ABC’D’ bằng

A. \(\frac{{{a^3}}}{3}\).

B. \(\frac{{{a^3}}}{2}\).

C. \(\frac{{{a^3}}}{6}\).

D. \(\frac{{2{a^3}}}{3}\).

Phương pháp giải - Xem chi tiết

Cách 1: Tính thể tích phần bù

Ta có \({V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}} \)

\(-\left( {{V_{B'.ABC}} + {V_{C.B'C'D'}} + {V_{D'.ACD}} + {V_{A.A'B'D'}}} \right)\).

Mà \({V_{ABCD.A'B'C'D'}} = {a^3}\), và:

\({V_{B'.ABC}} = {V_{C.B'C'D'}} = {V_{D'.ACD}} = {V_{A.A'B'D'}} \)

\(= \frac{1}{3}.A'A.{S_{A'B'D'}} = \frac{1}{3}.a.\frac{1}{2}{a^2} = \frac{1}{6}{a^3}\).

\( \Rightarrow {V_{ACB'D'}}\).

Cách 2: Sử dụng công thức:

\({V_{ACB'D'}} = \frac{1}{6}AC.B'D'.d\left( {AC,B'D'} \right).\sin \left( {AC,B'D'} \right)\).

Lời giải chi tiết

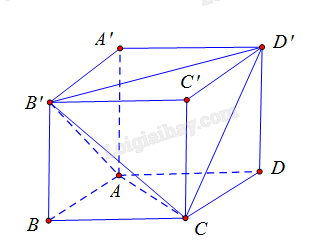
Cách 1:

Ta có \({V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}} - \left( {{V_{B'.ABC}} + {V_{C.B'C'D'}} + {V_{D'.ACD}} + {V_{A.A'B'D'}}} \right)\).

Mà \({V_{ABCD.A'B'C'D'}} = {a^3}\) và \({V_{B'.ABC}} = {V_{C.B'C'D'}} = {V_{D'.ACD}} = {V_{A.A'B'D'}} = \frac{1}{3}.A'A.{S_{A'B'D'}}\)

\(= \frac{1}{3}.a.\frac{1}{2}{a^2} = \frac{1}{6}{a^3}\).

Do đó \({V_{ACB'D'}} = {a^3} - \frac{4}{6}{a^3} = \frac{{{a^3}}}{3}\).

Cách 2: Sử dụng công thức \({V_{ACB'D'}} = \frac{1}{6}AC.B'D'.d\left( {AC,B'D'} \right).\sin \left( {AC,B'D'} \right)\).

\({V_{ACB'D'}} = \frac{1}{6}a\sqrt 2 .a\sqrt 2 .a.\sin {90^ \circ } = \frac{{{a^3}}}{3}\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Group 2K9 Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store