Bài 53 trang 165 SBT toán 9 tập 1

Giải bài 53 trang 165 sách bài tập toán 9. Tính diện tích tam giác đều ABC ngoại tiếp đường tròn (I; r).

Đề bài

Tính diện tích tam giác đều \(ABC\) ngoại tiếp đường tròn \((I; r).\)

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức:

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Giao ba đường phân giác trong của tam giác là điểm cách đều các cạnh tam giác (tâm đường tròn nội tiếp tam giác).

+) Trong tam giác đều, giao ba đường phân giác cũng là giao ba đường trung tuyến, trung trực, đường cao.

+) Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối.

Lời giải chi tiết

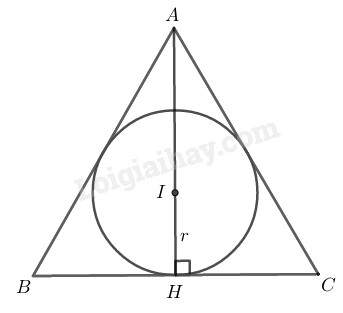
Gọi \(H\) là tiếp điểm của đường tròn \((I)\) với \(BC.\)

Ta có: \(IH ⊥ BC\) (tính chất tiếp tuyến)

Vì \(I\) là tâm đường tròn nội tiếp tam giác \(ABC\) nên \(AI\) là tia phân giác của góc \(BAC.\)

Tam giác \(ABC\) đều nên \(AI\) cũng là đường cao của tam giác \(ABC.\) Khi đó \(A, I, H\) thẳng hàng.

Khi đó đường cao AH cũng là đường trung tuyến của tam giác đều ABC nên ta có: \(HB = HC=\dfrac{BC}2\) ( tính chất tam giác đều)

Tam giác \(ABC\) đều nên \(I\) cũng là trọng tâm của tam giác \(ABC.\)

Suy ra: \(AH = 3.HI = 3.r\)

\(\widehat {HAB} =\displaystyle {1 \over 2}\widehat {BAC}\)\( = \displaystyle{1 \over 2}.60^\circ = 30^\circ \) (vì \(AH\) là tia phân giác của góc \(BAC\))

Tam giác \(ABH\) vuông tại \(H\) nên ta có:

\(BH = AH.tan\widehat {HAB} = 3{\rm{r}}.tan{30^0} \)\(=\displaystyle 3{\rm{r}}.{{\sqrt 3 } \over 3} = r\sqrt 3 \)

Mà: \(BC = 2.BH = 2r\sqrt 3 \)

Vậy \({S_{ABC}} =\displaystyle {1 \over 2}AH.BC \)\(= \displaystyle{1 \over 2}.3r.2r\sqrt 3 = 3{r^2}\sqrt 3 \) \((đvdt)\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 9 phiếu

Bài tiếp theo

Bài 54 trang 165 SBT toán 9 tập 1
Giải bài 54 trang 165 sách bài tập toán 9. Cho đường tròn (O; 3cm) và điểm A có AO = 5cm. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Gọi H là giao điểm của AO và BC...
Bài 55 trang 165 SBT toán 9 tập 1
Giải bài 55 trang 165 sách bài tập toán 9. Cho đường tròn (O; 2cm), các tiếp tuyến AB và AC kẻ từ A đến đường tròn vuông góc với nhau tại A (B và C là các tiếp điểm)...
Bài 56 trang 165 SBT toán 9 tập 1
Giải bài 56 trang 165 sách bài tập toán 9. Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn (A ; AH). Kẻ các tiếp tuyến BD, CE với đường tròn (D, E là các tiếp điểm khác H). Chứng minh rằng:...
Bài 57 trang 165 SBT toán 9 tập 1
Giải bài 57 trang 165 sách bài tập toán 9. Chứng minh rằng nếu tam giác ABC có chu vi 2p,bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức: S=p.r
Bài 58 trang 165 SBT toán 9 tập 1
Giải bài 58 trang 165 sách bài tập toán 9. Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D, E...
Bài 59 trang 165 SBT toán 9 tập 1
Giải bài 59 trang 165 sách bài tập toán 9. Cho tam giác ABC vuông tại A. Gọi R là bán kính của đường tròn ngoại tiếp, r là bán kính của đường tròn nội tiếp tam giác ABC. Chứng minh rằng:...
Bài 60 trang 166 SBT toán 9 tập 1
Giải bài 60 trang 166 sách bài tập toán 9. Cho tam giác ABC, đường tròn (K) bằng tiếp góc trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC = a, AC = b, AB = c. Chứng minh rằng:...
Bài 61* trang 166 SBT toán 9 tập 1
Giải bài 61* trang 166 sách bài tập toán 9. Cho nửa hình tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C, D.
Bài 62* trang 166 SBT toán 9 tập 1
Giải bài 62* trang 166 sách bài tập toán 9. Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB)...
Bài 63* trang 166 SBT toán 9 tập 1
Giải bài 63* trang 166 sách bài tập toán 9. Cho tam giác ABC vuông tại A. Đường tròn nội tiếp tam giác ABC tiếp xúc với BC tại D. Chứng minh rằng:...
Bài 6.1 phần bài tập bổ sung trang 166 SBT toán 9 tập 1
Giải bài 6.1 phần bài tập bổ sung trang 166 sách bài tập toán 9. Độ dài mỗi cạnh của tam giác đều ngoại tiếp đường tròn (O ; r) bằng...
Bài 6.2 phần bài tập bổ sung trang 167 SBT toán 9 tập 1
Giải bài 6.2 phần bài tập bổ sung trang 167 sách bài tập toán 9. Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Đường thẳng đi qua O và song song với AB cắt AC tại D. Đường tròn đi qua O và song song với AC cắt AB ở E. Tứ giác ADOE là hình gì ?
Bài 6.3 phần bài tập bổ sung trang 167 SBT toán 9 tập 1
Giải bài 6.3 phần bài tập bổ sung trang 167 sách bài tập toán 9. Từ điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn. Kẻ dây CD song song với AB. Chứng minh rằng BC = BD.
Bài 52 trang 165 SBT toán 9 tập 1
Giải bài 52 trang 165 sách bài tập toán 9. Cho đường tròn (I) nội tiếp tam giác ABC. Các tiếp điểm trên AC, AB theo thứ tự là D, E. Cho BC = a, AC = b, AB = c. Tính độ dài các đoạn tiếp tuyến AD, AE theo a, b, c.
Bài 51 trang 164 SBT toán 9 tập 1
Giải bài 51 trang 164 sách bài tập toán 9. Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax,By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N.
Bài 50 trang 164 SBT toán 9 tập 1
Giải bài 50 trang 164 sách bài tập toán 9. Cho góc xOy khác góc bẹt, điểm A nằm trên tia Ox. Dựng đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy.
Bài 49 trang 164 SBT toán 9 tập 1
Giải bài 49 trang 164 sách bài tập toán 9. Cho đường tròn (O), điểm M nằm bên ngoài đường tròn. Kẻ tiếp tuyến MD, ME với đường tròn (D, E là các tiếp điểm). Qua điểm I thuộc cung nhỏ DE, kẻ tiếp tuyến với đường tròn, cắt MD và ME theo thứ tự ở P và Q. Biết MD = 4cm, tính chu vi tam giác MPQ.
Bài 48 trang 164 SBT toán 9 tập 1
Giải bài 48 trang 164 sách bài tập toán 9. Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M,N là các tiếp điểm)...