Giải bài 5 trang 56 Chuyên đề học tập Toán 10 – Cánh diều

Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để truyền tín hiệu cho máy bay hoặc tàu thủy hoạt động trên biển. Trong hệ thống đó có hai đài vô tuyến đặt lần lượt tại địa điểm A và địa điểm B, khoảng cách AB = 650 km (Hình 18). Giả sử có một con tàu chuyển động trên biển với quỹ đạo là hypebol nhận A và B là hai tiêu điểm.

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để truyền tín hiệu cho máy bay hoặc tàu thủy hoạt động trên biển. Trong hệ thống đó có hai đài vô tuyến đặt lần lượt tại địa điểm A và địa điểm B, khoảng cách AB = 650 km (Hình 18). Giả sử có một con tàu chuyển động trên biển với quỹ đạo là hypebol nhận A và B là hai tiêu điểm.

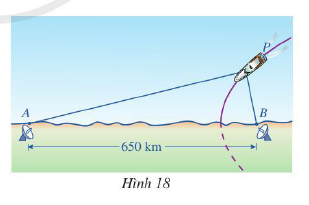
Khi đang ở vị trí P, máy thu tín hiệu trên con tàu chuyển đổi chênh lệch thời gian nhận các tín hiệu từ A và B thành hiệu khoảng cách \(\left| {PA - PB} \right|\). Giả sử thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s. Vận tốc di chuyển của tín hiệu là \({3.10^8}\) m/s.

a) Lập phương trình hypebol mô tả quỹ đạo chuyển động của con tàu

b) Chứng tỏ rằng tại mọi thời điểm trên quỹ đạo chuyển động thì thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A luôn là 0,0012 s.

Lời giải chi tiết

Vì thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A là 0,0012 s nên tại thời điểm đó \(PA - PB = \left( {{{3.10}^8}} \right).0,0012 = 360.000\left( m \right) = 360\left( {km} \right)\)

Vì con mày chuyển động với quỹ đạo là hypebol nhận A và B là hai tiêu điểm nên\(\left| {PA - PB} \right| = 360\left( {km} \right)\) với mọi vị trí của P

Chọn hệ trục tọa độ sao cho gốc tọa độ trùng với trung điểm của AB và trục Ox trùng với AB, đơn vị trên hai trục là km thì hypebol này có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\)

Vì \(\left| {PA - PB} \right| = 360\) nên \(2a = 360 \Rightarrow a = 180\)

Theo đề bài, \(AB = 650 \Rightarrow 2c = 650 \Rightarrow c = 325\)

Ta có: \({b^2} = {c^2} - {a^2} = {325^2} - {180^2} = 73225\)

Vậy phương trình hypebol có dạng \(\frac{{{x^2}}}{{32400}} - \frac{{{y^2}}}{{73225}} = 1\)

b) Vì con tàu chỉ chuyển động ở nhánh bên phải trục Oy của hypebol nên ta PB < PA với mọi vị trí của P. Do đó tàu luôn nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A.

Gọi \({t_1}\) là thời gian để tàu nhận được tín hiệu từ A, \({t_2}\) là thời gian để tàu nhận được tín hiệu từ B thì \({t_1} = \frac{{PA}}{v},{t_2} = \frac{{PB}}{v}\) với v là vận tốc di chuyển của tín hiệu.

Khi đó, ta có:

\({t_1} - {t_2} = \frac{{PA - PB}}{v} = \frac{{360000}}{{{{3.10}^8}}} = 0,0012\left( s \right)\)

Vậy thời gian con tàu nhận được tín hiệu từ B trước khi nhận được tín hiệu từ A luôn là 0,0012 s.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 56 Chuyên đề học tập Toán 10 – Cánh diều
Trong mặt phẳng tọa độ Oxy, cho hypebol (H): \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\). Lập phương trình chính tắc của hypebol (E), biết rằng (E) có các tiêu điểm là tiêu điểm của (H) và các đỉnh của hình chữ nhật cơ sở của (H) cũng nằm trên (E)
Giải bài 3 trang 56 Chuyên đề học tập Toán 10 – Cánh diều
Trong mặt phẳng tọa độ Oxy, cho hypebol có phương trình chính tắc là \({x^2} - {y^2} = 1\). Chứng minh rằng hai đường tiệm cận của hypebol vuông góc với nhau.
Giải bài 2 trang 56 Chuyên đề học tập Toán 10 – Cánh diều
Trong mặt phẳng tọa độ Oxy, cho hypebol có phương trình chính tắc là \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\)
Giải bài 1 trang 56 Chuyên đề học tập Toán 10 – Cánh diều
Viết phương trình chính tắc của hypebol (H), biết:
Giải mục 6 trang 55 Chuyên đề học tập Toán 10 - Cánh diều
Cho hypebol (H) có một đỉnh là \({A_1}( - 4;0)\) và tiêu cự là 10. Viết phươn trình chính tắc và vẽ hypebol (H).
Giải mục 5 trang 53, 54 Chuyên đề học tập Toán 10 - Cánh diều
Cho hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\).
Giải mục 4 trang 53 Chuyên đề học tập Toán 10 - Cánh diều
Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho \(\left| {M{F_1} - M{F_2}} \right| = 2a\), ở đó \({F_1}{F_2} = 2c\) với \(c > a > 0\).
Giải mục 3 trang 52 Chuyên đề học tập Toán 10 - Cánh diều
Viết phương trình chính tắc của hypebol, biết độ trục ảo bằng 6 và tâm sai bằng \(\frac{5}{4}.\)
Giải mục 2 trang 50, 51 Chuyên đề học tập Toán 10 - Cánh diều
a) Quan sát điểm \(M\left( {x;y} \right)\) thuộc hypebol (H) (Hình 15) và chứng tỏ rằng \(x \le - a\) hoặc \(x \ge a\)
Giải mục 1 trang 49 Chuyên đề học tập Toán 10 - Cánh diều
Trong mặt phẳng tọa độ \(Oxy\), ta xét hypebol (H) với phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) trong đó \(a > 0,b > 0\) (Hình 13)