Giải bài 3 trang 67 Chuyên đề học tập Toán 10 – Cánh diều

Cho parabol có phương trình chính tắc \({y^2} = 2x\). Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó.

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Cho parabol có phương trình chính tắc \({y^2} = 2x\). Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó.

Phương pháp giải - Xem chi tiết

Cho parabol có PTCT: \({y^2} = 2px\) trong đó \(p > 0\)

+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)

+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)

Lời giải chi tiết

+ Ta có: \(2p = 2 \Rightarrow p = 1\)

Tiêu điểm của parabol (P) là \(F\left( {\frac{1}{2};0} \right)\)

Đường chuẩn: \(\Delta :x = - \frac{1}{2}\)

+ Vẽ parabol

Để vẽ parabol (P): \({y^2} = 2x\) ta có thể làm như sau:

Bước 1: Lập bảng giá trị

x	0	0,5	0,5	2	2	4,5	4,5
y	0	-1	1	-2	2	-3	3

Chú ý rằng tương ứng với mỗi giá trị dương của x có hai giá trị của y đối nhau

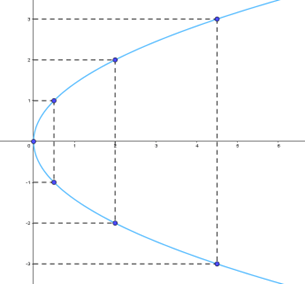
Bước 2: Vẽ các điểm cụ thể mà hoành độ và tung độ được xác định như trong bảng giá trị

Bước 3: Vẽ đường parabol bên phải trục Oy, đỉnh O, trục đối xứng là Ox, parabol đi qua các điểm được vẽ ở Bước 2

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 67 Chuyên đề học tập Toán 10 – Cánh diều
Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :x = - 5\) và điểm \(F\left( { - 4;0} \right)\). Lấy 3 điểm \(A\left( { - 3;1} \right),B\left( {2;8} \right),C\left( {0;3} \right)\)
Giải bài 5 trang 67 Chuyên đề học tập Toán 10 – Cánh diều
Vệ tinh nhân tạo lần đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1.342 dặm (1 dặm xấp xỉ 1.609 km). Tìm tâm sai của quỹ đạo đó, biết bán kinh của Trái Đất xấp xỉ 4.000 dặm
Giải bài 6 trang 67 Chuyên đề học tập Toán 10 – Cánh diều
Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có một trong hai tiêu điểm là tâm của Mặt Trời. Biết elip này có bán trục lớn \(a \approx 5,{906.10^6}\left( {km} \right)\) và tâm sai \(e \approx 0,249\) (Nguồn: http://vi.wikimedia.org)
Giải bài 7 trang 67 Chuyên đề học tập Toán 10 – Cánh diều
Cho đường thẳng \(\Delta \) và điểm O sao cho khoảng cách từ O đến \(\Delta \) là OH = 1 (Hình 39). Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên \(\Delta \). Chứng minh tập hợp các điểm M trong mặt phẳng sao cho \(M{K^2} - M{O^2} = 1\) là một đường parabol.
Giải bài 2 trang 67 Chuyên đề học tập Toán 10 – Cánh diều
Các đường conic có phương trình như sau là đường elip hay hypebol? Tìm độ dài các trục, tọa độ tiêu điểm, tiêu cự, tâm sai của các đường conic đó.
Giải bài 1 trang 66 Chuyên đề học tập Toán 10 – Cánh diều
Cho hình chữ nhật ABCD với bốn đỉnh \(A\left( { - 4;3} \right),B\left( {4;3} \right),C\left( {4; - 3} \right),D\left( { - 4; - 3} \right).\)
Giải mục 1 trang 60 Chuyên đề học tập Toán 10 - Cánh diều
Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.