SBT Toán 12 - giải SBT Toán 12 - Cánh diều Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số ..

Giải bài 45 trang 20 sách bài tập toán 12 - Cánh diều


Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông có độ dài cạnh 4 m như Hình 9 với hai mép tấm bạt sát mặt đất. Tính khoảng cách \(AB\) để khoảng không gian trong lều là lớn nhất.

Đề bài

Nhóm bạn Đức dựng trên một khu đất bằng phẳng một chiếc lều từ một tấm bạt hình vuông có độ dài cạnh 4 m như Hình 9 với hai mép tấm bạt sát mặt đất. Tính khoảng cách \(AB\) để khoảng không gian trong lều là lớn nhất.

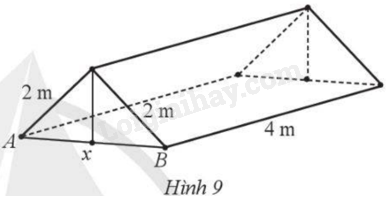
Phương pháp giải - Xem chi tiết

Sử dụng công thức tính thể tích hình lăng trụ để tính thể tích \(V\left( x \right)\) của không gian trong lều, sau đó tìm giá trị lớn nhất của hàm số \(V\left( x \right)\).

Lời giải chi tiết

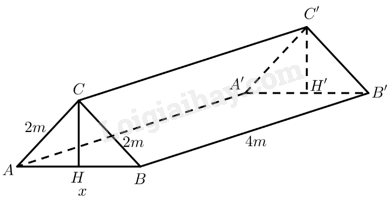
Giả sử lều dựng lên được hình lăng trụ đứng \(ABC.A'B'C'\) với \(AC = BC = 2,BB' = 4,\)\(AB = x\left( {0 < x < 4} \right)\).

\(AH = \frac{x}{2} \Rightarrow CH = \sqrt {A{C^2} - A{H^2}}  = \sqrt {4 - \frac{{{x^2}}}{4}} \)

\({S_{\Delta ABC}} = AB.CH = x.\sqrt {4 - \frac{{{x^2}}}{4}} \)

\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.BB' = x.\sqrt {4 - \frac{{{x^2}}}{4}} .4 = 2x\sqrt {16 - {x^2}} \).

Xét hàm số \(V\left( x \right) = 2x\sqrt {16 - {x^2}} \) trên khoảng \(\left( {0;4} \right)\)

Ta có: \(y' = {\left( {2x} \right)^\prime }\sqrt {16 - {x^2}}  + 2x.{\left( {\sqrt {16 - {x^2}} } \right)^\prime } = 2\sqrt {16 - {x^2}}  + 2x.\frac{{ - x}}{{\sqrt {16 - {x^2}} }} = \frac{{2\left( {8 - {x^2}} \right)}}{{\sqrt {16 - {x^2}} }}\)

\(y' = 0\) khi \(x = 2\sqrt 2 \).

Bảng biến thiên của hàm số:

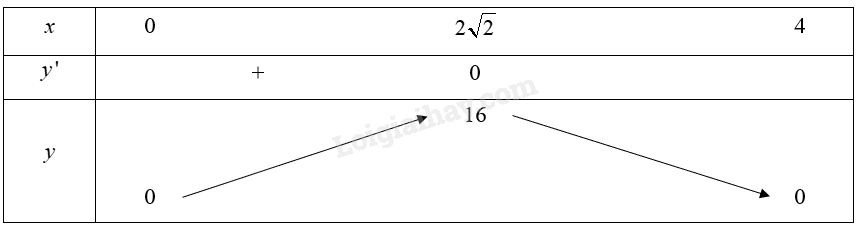
Căn cứ vào bảng biến thiên, ta có: \(\mathop {\max }\limits_{\left( {0;4} \right)} V\left( x \right) = 16\) tại \({\rm{x}} = 2\sqrt 2 \).

Vậy \(AB = 2\sqrt 2 \) thì khoảng không gian trong lều là lớn nhất.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải bài 46 trang 20 sách bài tập toán 12 - Cánh diều

    Nồng độ \(C\) của một loại hoá chất trong máu sau \(t\) giờ tiêm vào cơ thể được cho bởi công thức: \(C\left( t \right) = \frac{{3t}}{{27 + {t^3}}}\) với \(t \ge 0\) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Sau khoảng bao nhiêu giờ tiêm thì nồng độ của hoá chất trong máu là cao nhất?

  • Giải bài 47 trang 20 sách bài tập toán 12 - Cánh diều

    Khối lượng riêng \(S\left( {kg/d{m^3}} \right)\) của nước phụ thuộc vào nhiệt độ \(T\left( {^ \circ C} \right)\) được cho bởi công thức: \(S = \frac{{5,755}}{{{{10}^8}}}{T^3} - \frac{{8,521}}{{{{10}^6}}}{T^2} + \frac{{6,540}}{{{{10}^5}}}T + 0,99987\) với \(0 < T \le 25\) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). a) Tính khối lượng riêng của nước ở nhiệt độ \({25^ \circ }C\). b) Ở nhiệt độ nào thì khối lượng riêng của nước là lớn nhất?

  • Giải bài 44 trang 20 sách bài tập toán 12 - Cánh diều

    Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau: a) \(y = {3^x} + {3^{ - x}}\) trên đoạn \(\left[ { - 1;2} \right]\); b) \(y = x.{e^{ - 2{{\rm{x}}^2}}}\) trên đoạn \(\left[ {0;1} \right]\); c) \(y = \ln \left( {{x^2} + 2{\rm{x}} + 3} \right)\) trên đoạn \(\left[ { - 2;3} \right]\); d) \(y = - 3{\rm{x}} + 5 + x\ln {\rm{x}}\) trên đoạn \(\left[ {1;3} \right]\);

  • Giải bài 43 trang 20 sách bài tập toán 12 - Cánh diều

    Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau: a) \(y = \sin 2{\rm{x}} - x\) trên đoạn \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\); b) \(y = x + {\cos ^2}x\) trên đoạn \(\left[ {0;\frac{\pi }{4}} \right]\);

  • Giải bài 42 trang 19 sách bài tập toán 12 - Cánh diều

    Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau: a) \(y = 2{x^3} + 3{{\rm{x}}^2} - 12{\rm{x}} + 1\) trên đoạn \(\left[ { - 1;5} \right]\); b) \(y = {\left( {x - \sqrt 2 } \right)^2}.{\left( {x + \sqrt 2 } \right)^2}\) trên đoạn \(\left[ { - \frac{1}{2};2} \right]\); c) \(y = {x^5} - 5{{\rm{x}}^4} + 5{{\rm{x}}^3} + 1\) trên đoạn \(\left[ { - 1;2} \right]\); d) \(y = x + \frac{4}{x}\) trên đoạn \(\left[ {3;4} \right]\); e) \(y = \sqrt {x - 1} + \sqrt {3 - x} \); g) \(y = x\sqrt

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store