Giải bài 4 (7.15) trang 34, 35 vở thực hành Toán 7 tập 2

Cho các đa thức (A = 3{x^4} - 2{x^3} - x + 1;B = - 2{x^3} + 4{x^2} + 5x) và (C = - 3{x^4} + 2{x^2} + 5). Tính (A + B + C;A - B + C) và (A - B - C).

Đề bài

Cho các đa thức \(A = 3{x^4} - 2{x^3} - x + 1;B = - 2{x^3} + 4{x^2} + 5x\) và \(C = - 3{x^4} + 2{x^2} + 5\). Tính \(A + B + C;A - B + C\) và \(A - B - C\).

Phương pháp giải - Xem chi tiết

Để cộng (trừ) các đa thức:

Cách 1: Viết các đa thức trong dấu ngoặc và nối chúng bởi dấu “+” (hay “\( - \)”). Sau đó bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.

Cách 2: Đặt tính cộng (trừ) sao cho các hạng tử cùng bậc của các đa thức thì thẳng cột với nhau rồi cộng (trừ) theo từng cột.

Lời giải chi tiết

Để tính tổng \(A + B + C\), ta đặt tính như sau:

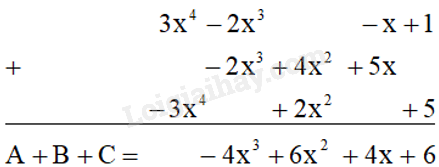
Để tính hai tổng còn lại, ta để ý rằng \(A - B + C = \left( {A - B} \right) + C\) và \(A - B - C = \left( {A - B} \right) - C\).

Vì vậy trước hết ta tính: \(A - B\):

\(A - B = \left( {3{x^4} - 2{x^3} - x + 1} \right) - \left( { - 2{x^3} + 4{x^2} + 5x} \right)\)

\( = 3{x^4} - 2{x^3} - x + 1 + 2{x^3} - 4{x^2} - 5x\)

\( = 3{x^4} + \left( { - 2{x^3} + 2{x^3}} \right) - 4{x^2} + \left( { - x - 5x} \right) + 1\)

\( = 3{x^4} - 4{x^2} - 6x + 1\)

Từ đó:

\(\left( {A - B} \right) + C = \left( {3{x^4} - 4{x^2} - 6x + 1} \right) + \left( { - 3{x^4} + 2{x^2} + 5} \right)\)

\( = \left( {3{x^4} - 3{x^4}} \right) + \left( { - 4{x^2} + 2{x^2}} \right) - 6x + \left( {1 + 5} \right)\)

\( = - 2{x^2} - 6x + 6\)

\(\left( {A - B} \right) - C = \left( {3{x^4} - 4{x^2} - 6x + 1} \right) - \left( { - 3{x^4} + 2{x^2} + 5} \right)\)

\( = 3{x^4} - 4{x^2} - 6x + 1 + 3{x^4} - 2{x^2} - 5\)

\( = \left( {3{x^4} + 3{x^4}} \right) + \left( { - 4{x^2} - 2{x^2}} \right) - 6x + \left( {1 - 5} \right)\)

\( = 6{x^4} - 6{x^2} - 6x - 4\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 (7.17) trang 36 vở thực hành Toán 7 tập 2
Trên một mảnh đất hình chữ nhật có chiều dài 65m, người ta định làm một bể bơi có chiều rộng là x mét, chiều dài gấp 3 lần chiều rộng. Sơ đồ và kích thước cụ thể (tính bằng mét) được cho trong hình bên. Tìm đa thức (biến x): a) Biểu thị diện tích của bể bơi. b) Biểu thị diện tích mảnh đất. c) Biểu thị diện tích phần đất xung quanh bể bơi.
Giải bài 6 (7.16) trang 35, 36 vở thực hành Toán 7 tập 2
Bạn Nam được phân công mua một số sách làm quà tặng trong buổi tổng kết cuối năm học của lớp. Nam dự định mua ba loại sách với giá bán như bảng sau. Giả sử Nam cần mua x cuốn sách khoa học, (x + 8) cuốn sách tham khảo và (x + 5) cuốn truyện tranh. a) Viết các đa thức biểu thị số tiền Nam phải trả cho từng loại sách. b) Tìm đa thức biểu thị tổng số tiền Nam phải trả để mua số sách đó.
Giải bài 5 trang 35 vở thực hành Toán 7 tập 2
Cho ba đa thức (A = 4{x^4} - 2 + 5{x^2} - x;B = 5x + 3 - 4{x^2} - 3{x^3}) và (C = 4{x^4} + 4x - 4{x^3} + {x^2}). a) Sắp xếp các đa thức trên theo lũy thừa giảm của biến. b) Tính (A + B - C). c) Tính giá trị của đa thức (A + B - C) tại (x = - 1).
Giải bài 3 (7.14) trang 34 vở thực hành Toán 7 tập 2
Cho hai đa thức (A = 6{x^4} - 4{x^3} + x - frac{1}{3}) và (B = - 3{x^4} - 2{x^3} - 5{x^2} + x + frac{2}{3}). Tính (A + B) và (A - B).
Giải bài 2 (7.13) trang 34 vở thực hành Toán 7 tập 2
Tìm hiệu sau bằng cách đặt tính trừ: (left( { - {x^3} - 5x + 2} right) - left( {3x + 8} right)).
Giải bài 1 (7.12) trang 33, 34 vở thực hành Toán 7 tập 2
Tìm tổng của hai đa thức sau bằng cách nhóm các hạng tử cùng bậc: ({x^2} - 3x + 2) và (4{x^3} - {x^2} + x - 1).
Giải câu hỏi trắc nghiệm trang 33 vở thực hành Toán 7 tập 2
Cho hai đa thức P và Q sao cho cả ba đa thức P, Q, (P + Q) đều khác đa thức không. Khi đó luôn xảy ra A. Bậc của (P + Q) lớn hơn bậc của P và của Q. B. Bậc của (P + Q) nhỏ hơn bậc của P và của Q. C. Bậc của (P + Q) bằng bậc của P hoặc bằng bậc của Q. D. Bậc của (P + Q) bằng bậc của P nếu bậc của P lớn hơn bậc của Q.