SBT Toán 11 - giải SBT Toán 11 - Cánh diều Bài 3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện ..

Giải bài 29 trang 100 sách bài tập toán 11 - Cánh diều


Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\)

Đề bài

Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), \(ABCD\) là hình thoi cạnh \(a\), \(AC = a\), \(SA = \frac{a}{2}\). Tính số đo của góc nhị diện \(\left[ {S,CD,A} \right]\).

Phương pháp giải - Xem chi tiết

Gọi \(E\) là hình chiếu của \(A\) trên \(CD\). Chứng minh rằng \(\widehat {SEA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {S,CD,A} \right]\), từ đó tính được số đo của góc nhị diện này.

Lời giải chi tiết

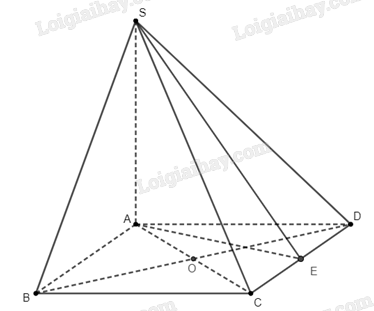
Gọi \(E\) là hình chiếu của \(A\) trên \(CD\). Do \(SA \bot \left( {ABCD} \right)\) nên ta suy ra \(SA \bot CD\). Do \(AE \bot CD\) nên ta suy ra \(\left( {SAE} \right) \bot CD\), điều này dẫn tới \(SE \bot CD\).

Như vậy do \(SE \bot CD\), \(AE \bot CD\) nên góc \(\widehat {SEA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {S,CD,A} \right]\).

Tam giác \(ACD\) đều (\(AC = CD = AD = a\)) nên ta suy ra \(AE = \frac{{a\sqrt 3 }}{2}\).

Xét tam giác \(SAE\) vuông tại \(A\), ta có \(\tan \widehat {SEA} = \frac{{SA}}{{AE}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{3}\).

Vậy \(\widehat {SEA} = {30^o}\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store