Giải bài 1.18 trang 15 sách bài tập toán 12 - Kết nối tri thức

Hai nguồn nhiệt đặt cách nhau \(s\) mét, một nguồn có cường độ \(a\) đặt ở điểm A và một nguồn có cường độ \(b\) đặt ở điểm B. Cường độ nhiệt tại điểm P nằm trên đoạn thẳng nối A và B được tính theo công thức \(I = \frac{a}{{{x^2}}} + \frac{b}{{{{\left( {s - x} \right)}^2}}},\) Trong đó \(x\) (m) là khoảng cách giữa P và A. Tại điểm nào giữa A và B, nhiệt độ sẽ thấp nhất?

Đề bài

Hai nguồn nhiệt đặt cách nhau \(s\) mét, một nguồn có cường độ \(a\) đặt ở điểm A và một nguồn có cường độ \(b\) đặt ở điểm B. Cường độ nhiệt tại điểm P nằm trên đoạn thẳng nối A và B được tính theo công thức

\(I = \frac{a}{{{x^2}}} + \frac{b}{{{{\left( {s - x} \right)}^2}}},\)

Trong đó \(x\) (m) là khoảng cách giữa P và A. Tại điểm nào giữa A và B, nhiệt độ sẽ thấp nhất?

Phương pháp giải - Xem chi tiết

Xét hàm số \(I = \frac{a}{{{x^2}}} + \frac{b}{{{{\left( {s - x} \right)}^2}}},{\rm{ }}0 \le x \le s\). Yêu cầu bài toán tương đương tìm \(x\) để hàm số đạt giá trị nhỏ nhất. Tính đạo hàm, lập bảng biến thiên của hàm số và đưa ra kết luận.

Lời giải chi tiết

Xét hàm số \(I = \frac{a}{{{x^2}}} + \frac{b}{{{{\left( {s - x} \right)}^2}}},{\rm{ }}0 \le x \le s\). Ta cần tìm \(x\) để hàm số đạt giá trị nhỏ nhất.

Ta có: \(I' = - \frac{{2a}}{{{x^3}}} + \frac{{2b}}{{{{\left( {s - x} \right)}^3}}} = \frac{{2\left[ {b{x^3} - a{{\left( {s - x} \right)}^3}} \right]}}{{{x^3}{{\left( {s - x} \right)}^3}}},{\rm{ }}0 \le x \le s\)

Khi đó \(I' = 0 \Leftrightarrow \frac{{2\left[ {b{x^3} - a{{\left( {s - x} \right)}^3}} \right]}}{{{x^3}{{\left( {s - x} \right)}^3}}} = 0 \Leftrightarrow 2\left[ {b{x^3} - a{{\left( {s - x} \right)}^3}} \right] = 0 \Leftrightarrow \frac{x}{{s - x}} = \frac{{\sqrt[3]{a}}}{{\sqrt[3]{b}}} \Leftrightarrow x = \frac{{s\sqrt[3]{a}}}{{\sqrt[3]{a} + \sqrt[3]{b}}}\).

Lập bảng biến thiên của hàm số:

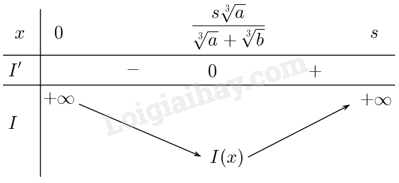
Từ bảng biến thiên suy ra hàm số đạt giá trị nhỏ nhất tại \(x = \frac{{s\sqrt[3]{a}}}{{\sqrt[3]{a} + \sqrt[3]{b}}}\).

Vậy tại điểm P trên đoạn AB các A một khoảng \(PA = x = \frac{{s\sqrt[3]{a}}}{{\sqrt[3]{a} + \sqrt[3]{b}}}\)(m) thì nhiệt độ thấp nhất.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 1.19 trang 16 sách bài tập toán 12 - Kết nối tri thức
Một vật được phóng lên trời theo một góc xiên (theta left( {{{45}^ circ } < theta < {{90}^ circ }} right)) so với phương ngang với vận tốc ban đầu là ({v_0}) (feet/giây) tính từ chân mặt phẳng nghiêng tạo một góc ({45^ circ }) so với phương ngang (xem hình vẽ). Nếu bỏ qua sức cản của không khí thì quãng đường R (tính bằng feet, 1 feet=0,3048 m) mà vật di chuyển lên mặt phẳng nghiêng được cho bởi hàm số (Rleft( theta right) = frac{{v_0^2sqrt 2 }}{{16}}cos theta left( {si
Giải bài 1.20 trang 16 sách bài tập toán 12 - Kết nối tri thức
Một chiếc xe nhỏ chuyển động không có ma sát, gắn vào tường bằng một lò xo (xem hình vẽ), được kéo ra khỏi vị trí đứng yên (10) cm rồi thả ra tại thời điểm ban đầu (t = 0) giây để chuyển động trong (4) giây. Vị trí (s) (cm) tại thời điểm (t) giây là (s = 10cos pi t).
Giải bài 1.17 trang 15 sách bài tập toán 12 - Kết nối tri thức
Giả sử một chiếc xe tải khi di chuyển với tốc độ (x) dặm/giờ sẽ tiêu thụ nhiên liệu ở mức (frac{1}{{200}}left( {frac{{2500}}{x} + x} right)) gallon/dặm. Nếu giá nhiên liệu là (3,6) USD/gallon thì chi phí nhiên liệu (C) (tính bằng USD) khi lái xe (200) dặm với tốc độ (x) dặm/giờ được cho bởi công thức (C = Cleft( x right) = 3,6 cdot left( {frac{{2500}}{x} + x} right)). Ở đây, dặm và gallon, là những đơn vị đo lường phổ biến của Mỹ. Biết rằng tốc độ (dặm/giờ) của xe tải t
Giải bài 1.16 trang 15 sách bài tập toán 12 - Kết nối tri thức
Lợi nhuận thu được (P) của một công ty khi dùng số tiền (s) chi cho quảng cáo được cho bởi công thức (P = Pleft( s right) = - frac{1}{{10}}{s^3} + 6{s^2} + 400,{rm{ s}} ge 0). Ở đây các số tiền được được tính bằng đơn vị nghìn USD. a) Tìm số tiền công ty phải chi cho quảng cáo để mang lại lợi nhuận tối đa. b) Lợi nhuận thu được của công ty thay đổi thế nào khi số tiền chi cho quảng cáo thay đổi?
Giải bài 1.15 trang 15 sách bài tập toán 12 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau: (fleft( x right) = left{ begin{array}{l}2x - 1,{rm{ }}0 le x le 2{x^2} - 5x + 9,{rm{ }}2 < x le 3.end{array} right.)
Giải bài 1.14 trang 14 sách bài tập toán 12 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (fleft( x right) = xsqrt {4 - {x^2}} , - 2 le x le 2); b) (fleft( x right) = x - cos x, - frac{pi }{2} le x le frac{pi }{2}).
Giải bài 1.13 trang 14 sách bài tập toán 12 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = - {x^3} + 3{x^2} + 2); b) (y = frac{{{x^2}}}{{{x^2} + 2}}).
Giải bài 1.12 trang 14 sách bài tập toán 12 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = 3{x^4} - 4{x^3}); b) (y = frac{{{x^2}}}{{x - 1}},x > 1).
Giải bài 1.11 trang 14 sách bài tập toán 12 - Kết nối tri thức
Sử dụng đồ thị dưới đây, xác định xem hàm số (y = fleft( x right)) có giá trị lớn nhất, giá trị nhỏ nhất hay cực trị tại mỗi điểm ({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8}) hay không.