-
CHƯƠNG 1: PHÉP NHÂN VÀ PHÉP CHIA ĐA THỨC
-
Chủ đề 1 : Phép nhân đa thức – Hằng đẳng thức đáng nhớ
-
Chủ đề 2 : Phân tích đa thức thành nhân tử
- 1. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- 2. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- 3. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- 4. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
- Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
-
Chủ đề 3: Phép chia đa thức
-
Ôn tập chương 1 - Phép nhân và phép chia đa thức
-
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
-
CHƯƠNG 1. TỨ GIÁC
-
Chủ đề 1 : Tứ giác – Hình thang
-
Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- 1. Đối xứng trục
- 2. Hình bình hành
- 3. Đối xứng tâm
- 4. Hình chữ nhật
- 5. Tập hợp các điểm cách đều một đường thẳng cho trước
- 6. Hình thoi
- 7. Hình vuông
- Bài tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
- Luyện tập - Chủ đề 2 : Hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông
-
Ôn tập chương 1 - Tứ giác
-
-
CHƯƠNG 2. ĐA GIÁC. DIỆN TÍCH ĐA GIÁC
-
CHƯƠNG 3 : PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN – GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH
-
CHƯƠNG 4. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
-
CHƯƠNG 3. TAM GIÁC ĐỒNG DẠNG
-
Chủ đề 1 : Định lí Thales
-
Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- 1. Khái niệm hai tam giác đồng dạng
- 2. Trường hợp đồng dạng thứ nhất (c.c.c)
- 3. Trường hợp đồng dạng thứ hai (c.g.c)
- 4. Trường hợp đồng dạng thứ ba (g.g)
- 5. Các trường hợp đồng dạng của tam giác vuông
- 6. Ứng dụng thực tế của tam giác đồng dạng
- Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
- Luyện tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng
-
-
CHƯƠNG 4 : HÌNH LĂNG TRỤ ĐỨNG – HÌNH CHÓP ĐỀU
-
ÔN TẬP CUỐI NĂM - TÀI LIỆU DẠY-HỌC TOÁN 8
Giải bài tập Tài liệu Dạy - học Toán lớp 8, Phát triển tư duy đột phá trong dạy học Toán 8
Luyện tập - Chủ đề 2 : Phân tích đa thức thành nhân tử
Luyện tập 8 trang 35 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Người ta làm một lối đi theo chiều dài và chiều rộng của một sân cỏ hình chữ nhật như hình sau.
Đề bài
Người ta làm một lối đi theo chiều dài và chiều rộng của một sân cỏ hình chữ nhật như hình sau. Em hãy tính chiều rộng x của lối đi. Biết rằng lối đi có diện tích bằng 46 m2, sân cỏ có chiều dài 15 m, chiều rộng 6 m.
Lời giải chi tiết
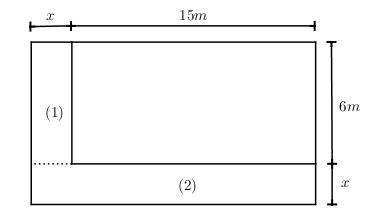
Chia lối đi thành hai hình chữ nhật như hình dưới.
Diện tích hình chữ nhật (1) của lối đi bằng \(6x\,\,\left( {{m^2}} \right)\)
Diện tích hình chữ nhật (2) của lối đi bằng \(\left( {15 + x} \right)x\,\,\left( {{m^2}} \right)\)
Diện tích lối đi bằng \(46{m^2}\) nên ta có:
\(\eqalign{ & 6x + \left( {15 + x} \right).x = 46 \cr & \,\,\,\,\,\,6x + 15x + {x^2} - 46 = 0 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x^2} + 21x - 46 = 0 \cr & \,\,\,\,\,\,{x^2} + 23x - 2x - 46 = 0 \cr & x\left( {x + 23} \right) - 2\left( {x + 23} \right) = 0 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\left( {x + 23} \right)\left( {x - 2} \right) = 0 \cr} \)
\(x + 23 = 0\) hoặc \(x - 2 = 0\)
\(x = - 23\) hoặc \(x = 2\)
Vì chiều rộng của lối đi là số dương nên \(x = 2\)
Vậy chiều rộng của lối đi là 2m.
Loigiaihay.com
Bình luận
Chia sẻ
- Luyện tập 9 trang 35 Tài liệu dạy – học Toán 8 tập 1
- Luyện tập 10 trang 35 Tài liệu dạy – học Toán 8 tập 1
- Luyện tập 7 trang 35 Tài liệu dạy – học Toán 8 tập 1
- Luyện tập 6 trang 35 Tài liệu dạy – học Toán 8 tập 1
- Luyện tập 5 trang 35 Tài liệu dạy – học Toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho Lớp 8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
