Trắc nghiệm Bài 48: Em làm được những gì Toán 4 Chân trời sáng tạo
Đề bài

Khi nhân số tự nhiên với \(10,\,100,\,\,1000,\,\,...\) ta chỉ việc viết thêm một, hai, ba, … chữ số \(0\) vào bên phải số đó. Đúng hay sai?

Điền số thích hợp vào ô trống:
\(37 \times 1000 = \)

Điền số thích hợp vào ô trống:
\(9000kg = \)
tạ.

$537 \times 97 - 12458{\rm{ }}\,...\,629 + 357 \times 106$
Dấu thích hợp điền vào chỗ chấm là:
A. \( > \)
B. \( < \)
C. \( = \)

Cho biểu thức: $a \times 47 + 153\times a$. Giá trị của biểu thức với $a = 148$ là:
A. \(29800\)
B. \(29600\)
C. \(29480\)
D. \(29250\)

Điền số thích hợp vào ô trống:
Tính bằng cách thuận tiện:
\(136 \times 73 + 136 \times 54 - 136 \times 27\)
$=$
$\times \,(73+54\,-$
$)$
$=$
$\times $
$=$

Điền số thích hợp vào ô trống:
Một hình vuông có chu vi là $9\,dm\,{\rm{ 6\,c}}m$.
Vậy diện tích hình vuông đó là
\(\,c{m^2}\).

\(8{m^2}\,\,5d{m^2}\,\,\, = \,\,\,\,...\,\,d{m^2}\).
Số thích hợp điền vào chỗ chấm là:
A. \(8005\)
B. \(850\)
C. \(805\)
D. \(85\)

Một mảnh vườn thu hoạch được $275$ sọt cam, mỗi sọt cam nặng $48kg.$ Sau khi bán người ta thấy còn lại \(118\) sọt cam. Biết mỗi ki-lô-gam cam bán với giá \(22\,500\) đồng. Hỏi người ta đã thu được bao nhiêu tiền bán cam?
A. \(127\,\,440\,\,000\) đồng
B. \(168\,\,760\,\,000\) đồng
C. \(169\,\,560\,\,000\) đồng
D. \(175\,\,780\,\,000\) đồng
 Bác Minh trồng ngô trên một mảnh vườn hình chữ nhật có chu vi $546m$, chiều rộng kém chiều dài $23m.$ Tính số tạ ngô bác Minh thu được trên mảnh vườn đó, biết rằng cứ $100m^2$ thì thu được $60kg$ ngô.
Bác Minh trồng ngô trên một mảnh vườn hình chữ nhật có chu vi $546m$, chiều rộng kém chiều dài $23m.$ Tính số tạ ngô bác Minh thu được trên mảnh vườn đó, biết rằng cứ $100m^2$ thì thu được $60kg$ ngô.
A. \(111\) tạ
B. \(145\) tạ
C. \(1450\) tạ
D. \(11100\) tạ
Lời giải và đáp án

Khi nhân số tự nhiên với \(10,\,100,\,\,1000,\,\,...\) ta chỉ việc viết thêm một, hai, ba, … chữ số \(0\) vào bên phải số đó. Đúng hay sai?
Xem lại lí thuyết về cách nhân số tự nhiên với \(10,\,100,\,\,1000,\,\,...\)
Khi nhân số tự nhiên với \(10,\,100,\,\,1000,\,\,...\) ta chỉ việc viết thêm một, hai, ba, … chữ số \(0\) vào bên phải số đó.
Vậy khẳng định đã cho là đúng.

Điền số thích hợp vào ô trống:
\(37 \times 1000 = \)
\(37 \times 1000 = \)
Áp dụng cách nhân số tự nhiên với \(10,\,100,\,\,1000,\,\,...\): Khi nhân số tự nhiên với \(10,\,100,\,\,1000,\,\,...\) ta chỉ việc viết thêm một, hai, ba, … chữ số \(0\) vào bên phải số đó.
Khi nhân số tự nhiên với \(10,\,100,\,\,1000,\,\,...\) ta chỉ việc viết thêm một, hai, ba, … chữ số \(0\) vào bên phải số đó.
Do đó ta có: \(37 \times 1000 = 37000\)
Vậy đáp án đúng điền vào ô trống là \(37000\).

Điền số thích hợp vào ô trống:
\(9000kg = \)
tạ.
\(9000kg = \)
tạ.
- Đổi \(1\) tạ sang đơn vị ki-lô-gam: \(1\) tạ \( = \,\,100kg\).
- Để đổi \(9000kg\) sang đơn vị tấn ta thực hiện phép tính: \(9000:100\).
Ta có: \(100kg = 1\) tạ.
Nhẩm: \(9000:100 = 90\).
Do đó: \(9000kg = 90\) tạ.
Vậy đáp án đúng điền vào ô trống là \(90\).

$537 \times 97 - 12458{\rm{ }}\,...\,629 + 357 \times 106$
Dấu thích hợp điền vào chỗ chấm là:
A. \( > \)
B. \( < \)
C. \( = \)
A. \( > \)
Tính giá trị biểu thức ở hai vế rồi so sánh kết quả với nhau.
Biểu thức có phép cộng, phép trừ và phép nhân thì ta thực hiện phép nhân trước, thực hiện phép cộng, trừ sau.
Ta có
+) $537 \times 97 - 12458= 52089 - 12458= 39631$
+) $629+ 357 \times 106= 629 + 37842=38471$
Mà: \(39631 > 38471\).
Vậy $537 \times 97 - 12458\,\,{\rm{ > }}\,\,629+ 357 \times 106$.

Cho biểu thức: $a \times 47 + 153\times a$. Giá trị của biểu thức với $a = 148$ là:
A. \(29800\)
B. \(29600\)
C. \(29480\)
D. \(29250\)
B. \(29600\)
Thay $a = 148$ vào biểu thức $\;a \times 47 + \;153\; \times a$ rồi tính giá trị biểu thức đó.
Nếu $a = 148$ thì:
$\begin{array}{l}a \times 47 + 153 \times a \\= 148 \times 47 + 153 \times 148 \\= 148 \times 47 + 148 \times 153\\ = 148 \times (47 + 153) \\= 148 \times 200 = 29600\end{array}$
Vậy với $a = 148$ thì giá trị của biểu thức $a \times 47 + 153 \times a$ là \(29600\).

Điền số thích hợp vào ô trống:
Tính bằng cách thuận tiện:
\(136 \times 73 + 136 \times 54 - 136 \times 27\)
$=$
$\times \,(73+54\,-$
$)$
$=$
$\times $
$=$
Tính bằng cách thuận tiện:
\(136 \times 73 + 136 \times 54 - 136 \times 27\)
$=$
$\times \,(73+54\,-$
$)$
$=$
$\times $
$=$
Áp dụng công thức: \(a \times b + a \times c - a \times d = a \times (b + c - d)\)
\(136 \times 73 + 136 \times 54 - 136 \times 27\)
\( = 136 \times \left( {73 + 54 - 27} \right)\)
\( = 136 \times 100\)
\( = 13600\)
Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới, từ trái sang phải là \(136\,;\,\,27\,;\,\,136\,;\,\,100\,;\,\,13600\).

Điền số thích hợp vào ô trống:
Một hình vuông có chu vi là $9\,dm\,{\rm{ 6\,c}}m$.
Vậy diện tích hình vuông đó là
\(\,c{m^2}\).
Một hình vuông có chu vi là $9\,dm\,{\rm{ 6\,c}}m$.
Vậy diện tích hình vuông đó là
\(\,c{m^2}\).
- Đổi $9dm\,{\rm{ 6c}}m$ sang đơn vị đo là \(cm\).
- Tính độ dài cạnh hình vuông ta lấy chu vi chia cho \(4\).
- Tính diện tích hình vuông ta lấy độ dài cạnh nhân với độ dài cạnh.
Độ dài cạnh của hình vuông đó là:
\(96:4 = 24\,\,(cm)\)
Diện tích hình vuông đó là:
\(24\times 24 = 576\,\,(c{m^2})\)
Đáp số: \(576c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(576\).

\(8{m^2}\,\,5d{m^2}\,\,\, = \,\,\,\,...\,\,d{m^2}\).
Số thích hợp điền vào chỗ chấm là:
A. \(8005\)
B. \(850\)
C. \(805\)
D. \(85\)
C. \(805\)
Áp dụng tính chất: \(1{m^2} = 100d{m^2}\) để đổi \(8{m^2}\) sang đơn vị \(d{m^2}\) rồi cộng thêm \(5d{m^2}\).
Ta có \(1{m^2} = 100d{m^2}\) nên \(8{m^2} = 800d{m^2}\).
Do đó \(8{m^2}\,5d{m^2} = 8{m^2} + 5d{m^2} = 800d{m^2} + 5d{m^2} = 805d{m^2}\).
Vậy: \(8{m^2}\,5d{m^2} = 805d{m^2}\).

Một mảnh vườn thu hoạch được $275$ sọt cam, mỗi sọt cam nặng $48kg.$ Sau khi bán người ta thấy còn lại \(118\) sọt cam. Biết mỗi ki-lô-gam cam bán với giá \(22\,500\) đồng. Hỏi người ta đã thu được bao nhiêu tiền bán cam?
A. \(127\,\,440\,\,000\) đồng
B. \(168\,\,760\,\,000\) đồng
C. \(169\,\,560\,\,000\) đồng
D. \(175\,\,780\,\,000\) đồng
C. \(169\,\,560\,\,000\) đồng
- Tính số sọt cam đã bán ta lấy tổng số sọt cam trừ đi số sọt cam còn lại.
- Tính số ki-lô-gam cam đã bán ta lấy số cam của một sọt nhân với số sọt cam đã bán.
- Tính số tiền thu được khi bán cam ta lấy số tiền khi bán một ki-lô-gam cam nhân với số ki-lô-gam cam đã bán.
Người ta đã bán số sọt cam là:
$275 - 118 = {\rm{ }}157\;$(sọt)
Người ta đã bán số ki-lô-gam cam là:
${\rm{48}} \times 157 = 7536\,\,(kg)$
Số tiền đã thu được sau khi bán cam là:
\(22\,\,500 \times 7536 = 169\,\,560\,\,000\) (đồng)
Đáp số: \(169\,\,560\,\,000\) đồng
 Bác Minh trồng ngô trên một mảnh vườn hình chữ nhật có chu vi $546m$, chiều rộng kém chiều dài $23m.$ Tính số tạ ngô bác Minh thu được trên mảnh vườn đó, biết rằng cứ $100m^2$ thì thu được $60kg$ ngô.
Bác Minh trồng ngô trên một mảnh vườn hình chữ nhật có chu vi $546m$, chiều rộng kém chiều dài $23m.$ Tính số tạ ngô bác Minh thu được trên mảnh vườn đó, biết rằng cứ $100m^2$ thì thu được $60kg$ ngô.
A. \(111\) tạ
B. \(145\) tạ
C. \(1450\) tạ
D. \(11100\) tạ
A. \(111\) tạ
- Tìm nửa chu vi ta lấy chu vi chia cho \(2\).
- Khi đó ta có tổng và hiệu của chiều dài và chiều rộng. Ta tìm chiều dài và chiều rộng theo công thức tìm hai số khi biết tổng và hiệu của hai số đó:
Số lớn = (Tổng + Hiệu) \(:\,2\) ;
Số bé = (Tổng – hiệu) \(:\,2\)
- Tìm diện tích mảnh vườn ta lấy số đo chiều dài nhân với số đo chiều rộng.
- Tìm diện tích mảnh vườn gấp \(100{m^2}\) bao nhiêu lần.
- Tìm trên cả mảnh vườn thu hoạch được bao nhiêu ki-lô-gam ngô và đổi sang đơn vị tạ.
Nửa chu vi mảnh vườn đó là:
\(546:2 = 273\,\,(m)\)
Ta có sơ đồ:
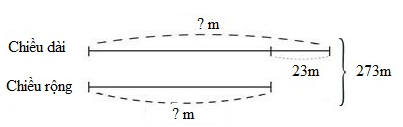
Chiều dài mảnh vườn đó là:
\((273 + 23):2 = 148\left( m \right)\)
Chiều rộng mảnh vườn đó là:
\(148 - 23 = 125\,\,\left( m \right)\)
Diện tích mảnh vườn đó là:
\(148 \times 125 = 18500\left( {{m^2}} \right)\)
\(18500{m^2}\) gấp \(100{m^2}\) số lần là:
\(18500:100 = 185\) (lần)
Trên cả mảnh vườn đó người ta thu hoạch được số ki-lô-gam ngô là:
\(60 \times 185 = 11100\,(kg)\)
\(11100kg = 111\) tạ
Đáp số: \(111\) tạ
Luyện tập và củng cố kiến thức Bài 49: Chia cho số có một chữ số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 50: Chia hai số có tận cùng là chữ số 0 Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 52: Chia cho số có hai chữ số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 53: Em làm được những gì Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 54: Hình bình hành Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 55: Hình thoi Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 57: Mi-li-mét vuông Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 58: Em làm được những gì Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 47: Nhân với số có hai chữ số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 46: Nhân các số có tận cùng là chữ số 0 Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 45: Nhân với 10, 100, 1 000,... Chia cho 10, 100, 1 000,... Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 44: Nhân với số có một chữ số Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 43: Em làm được những gì Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 42: Tìm hai số khi biết tổng và hiệu của hai số đó Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 41: Phép trừ các số tự nhiên Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 40: Phép cộng các số tự nhiên Toán 4 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 78: Ôn tập phân số và các phép tính Toán 4 Chân trời sáng tạo
- Trắc nghiệm Bài 78: Ôn tập hình học và đo lường Toán 4 Chân trời sáng tạo
- Trắc nghiệm Bài 78: Ôn tập số tự nhiên và các phép tính Toán 4 Chân trời sáng tạo
- Trắc nghiệm Bài 77: Em làm được những gì Toán 4 Chân trời sáng tạo
- Trắc nghiệm Bài 76: Tìm phân số của một số Toán 4 Chân trời sáng tạo










Danh sách bình luận