Lý thuyết Góc Toán 12 Cùng khám phá
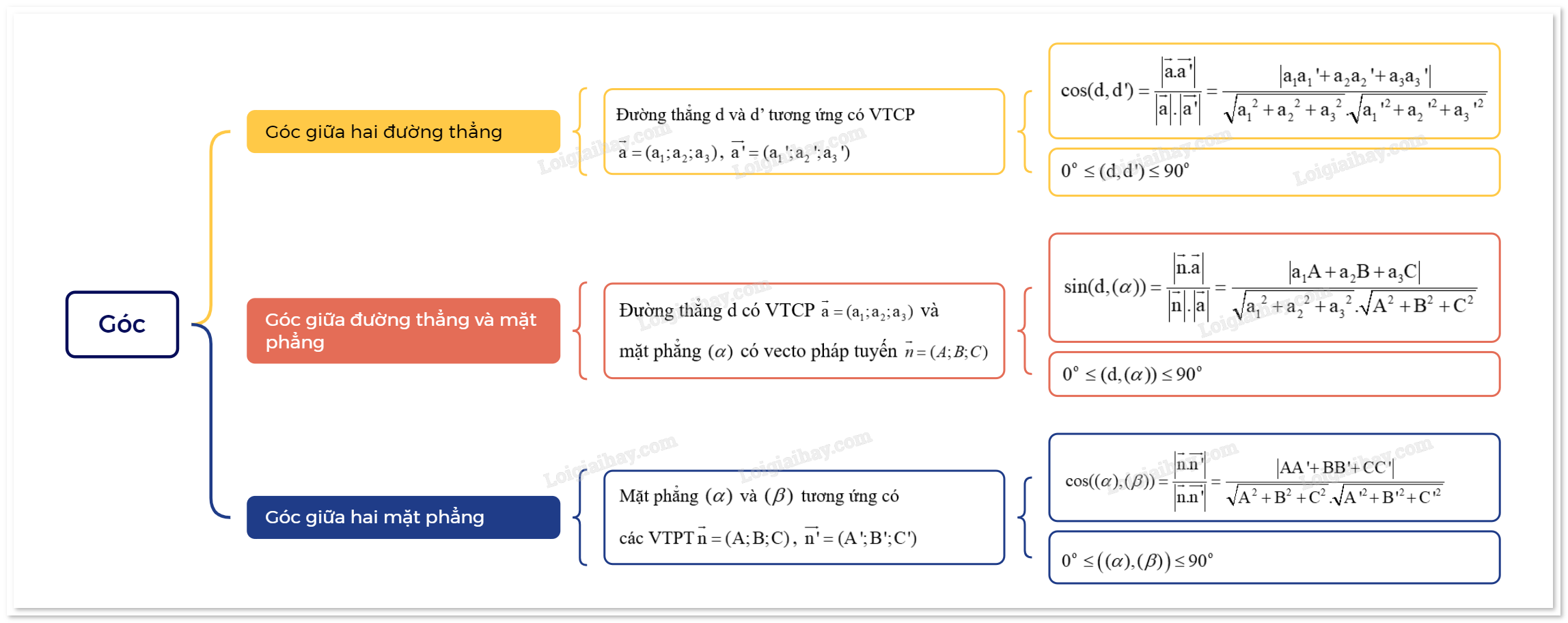
1. Góc giữa hai đường thẳng
1. Góc giữa hai đường thẳng
|
Trong không gian Oxyz, cho hai đường thẳng d và d’ tương ứng có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow {a'} = ({a_1}';{a_2}';{a_3}')\). Khi đó: \(\cos (d,d') = \frac{{\left| {\overrightarrow a .\overrightarrow {a'} } \right|}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow {a'} } \right|}} = \frac{{\left| {{a_1}{a_1}' + {a_2}{a_2}' + {a_3}{a_3}'} \right|}}{{\sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} .\sqrt {{a_1}{'^2} + {a_2}{'^2} + {a_3}{'^2}} }}\) |
Lưu ý:
+ \({0^o} \le (d,d') \le {90^o}\).
+ Nếu d//d’ hoặc d\( \equiv \)d’ thì \((d,d') = {0^o}\).
+ \(d \bot d' \Leftrightarrow (d,d') = {90^o}\).
Ví dụ: Trong không gian Oxyz, tính góc giữa hai đường thẳng:
d: \(\left\{ \begin{array}{l}x = 1 + t\\y = 3 - t\\z = 2t\end{array} \right.\) \((t \in \mathbb{R})\) và d’: \(\left\{ \begin{array}{l}x = t'\\y = 1 + 2t'\\z = 3 - t'\end{array} \right.\) \((t' \in \mathbb{R})\).
Giải:
Đường thẳng d và d’ lần lượt có các vecto chỉ phương là \(\overrightarrow a = (1; - 1;2)\) và \(\overrightarrow {a'} = (1;2; - 1)\).
Ta có \(\cos (d,d') = \frac{{\left| {\overrightarrow a .\overrightarrow {a'} } \right|}}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow {a'} } \right|}} = \frac{{\left| {1.1 - 1.2 + 2.( - 1)} \right|}}{{\sqrt {{1^2} + {{( - 1)}^2} + {2^2}} .\sqrt {{1^2} + {2^2} + {{( - 1)}^2}} }} = \frac{{\left| { - 3} \right|}}{6} = \frac{1}{2}\).
Vậy \((d,d') = {60^o}\).
2. Góc giữa đường thẳng và mặt phẳng
|
Trong không gian Oxyz, cho đường thẳng d có vecto chỉ phương \(\overrightarrow a = ({a_1};{a_2};{a_3})\) và mặt phẳng \((\alpha )\) có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\). Kí hiệu \(\left( {d,(\alpha )} \right)\) là góc giữa đường thẳng d và mặt phẳng \((\alpha )\). Khi đó: \(\sin (d,(\alpha )) = \frac{{\left| {\overrightarrow n .\overrightarrow a } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow a } \right|}} = \frac{{\left| {{a_1}A + {a_2}B + {a_3}C} \right|}}{{\sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} .\sqrt {{A^2} + {B^2} + {C^2}} }}\). |
Lưu ý:
+ \({0^o} \le (d,(\alpha )) \le {90^o}\).
+ Nếu \(d//(\alpha )\) hoặc \(d \subset (\alpha )\) thì \((d,(\alpha )) = {0^o}\).
+ \(d \bot (\alpha ) \Leftrightarrow (d,(\alpha )) = {90^o}\).
Ví dụ: Trong không gian Oxyz, tính góc giữa đường thẳng d: \(\frac{x}{{ - 1}} = \frac{y}{2} = \frac{{z - 1}}{{ - 1}}\) và mặt phẳng \((\alpha )\): \(x + y - 2z + 1 = 0\).
Giải:
Đường thẳng d có vectơ chỉ phương \(\overrightarrow a = ( - 1;2; - 1)\), mặt phẳng \((\alpha )\) có vectơ pháp tuyến \(\overrightarrow n = \left( {1;1; - 2} \right)\).
Ta có: \(\sin (d,(\alpha )) = \frac{{\left| {\overrightarrow n .\overrightarrow a } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow a } \right|}} = \frac{{\left| {( - 1).1 + 2.1( - 1).( - 2)} \right|}}{{\sqrt {{{( - 1)}^2} + {2^2} + {{( - 1)}^2}} .\sqrt {{1^2} + {1^2} + {{( - 2)}^2}} }} = \frac{1}{2}\).
Vậy \((d,(\alpha )) = {30^o}\).
3. Góc giữa hai mặt phẳng
|
Trong không gian Oxyz, cho hai mặt phẳng \((\alpha )\) và \((\beta )\) tương ứng có các vecto pháp tuyến \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {n'} = (A';B';C')\). Khi đó, góc giữa \((\alpha )\) và \((\beta )\), kí hiệu là \(\left( {(\alpha ),(\beta )} \right)\) được tính theo công thức: \(\cos ((\alpha ),(\beta )) = \frac{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}}{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}} = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\). |
Lưu ý:
+ \({0^o} \le \left( {(\alpha ),(\beta )} \right) \le {90^o}\).
+ Nếu \((\alpha )\)//\((\beta )\) hoặc \((\alpha ) \equiv (\beta )\) thì \(\left( {(\alpha ),(\beta )} \right) = {0^o}\).
+ \((\alpha ) \bot (\beta ) \Leftrightarrow \left( {(\alpha ),(\beta )} \right) = {90^o}\).
Ví dụ: Trong không gian Oxyz, tính góc giữa hai mặt phẳng: :\((\alpha )\) \(2x + 2y - 4z + 1 = 0\) và \((\beta )\): \(x - z - 5 = 0\).
Giải:
Mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\overrightarrow n = (2;2; - 4)\) và \(\overrightarrow {n'} = (1;0; - 1)\).
Ta có: \(\cos ((\alpha ),(\beta )) = \frac{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}}{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}} = \frac{{\left| {2.1 + 2.0 + ( - 4).( - 1)} \right|}}{{\sqrt {{2^2} + {2^2} + {{( - 4)}^2}} .\sqrt {{1^2} + {0^2} + {{( - 1)}^2}} }} = \frac{{\sqrt 3 }}{2}\).
Vậy \(\left( {(\alpha ),(\beta )} \right) = {30^o}\).
- Giải mục 1 trang 67, 68 SGK Toán 12 tập 2 - Cùng khám phá
- Giải mục 2 trang 68, 69 SGK Toán 12 tập 2 - Cùng khám phá
- Giải mục 3 trang 69, 70 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.24 trang 70 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.25 trang 70 SGK Toán 12 tập 2 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá













Danh sách bình luận