Giải mục 3 trang 69, 70 SGK Toán 12 tập 2 - Cùng khám phá
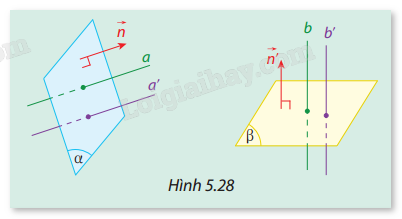
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 69 SGK Toán 12 Cùng khám phá
Cho hai mặt phẳng \((\alpha )\) và \((\beta )\) lần lượt có các vectơ pháp tuyến là \(\vec n\) và \(\vec n'\). Lấy hai đường thẳng \(a\), \(a'\) cùng vuông góc với \((\alpha )\), và hai đường thẳng \(b\), \(b'\) cùng vuông góc với \((\beta )\). (Hình 5.28) Hỏi hai góc \((a,b)\) và \((a',b')\) có bằng nhau không? Vì sao?
Phương pháp giải:
Sử dụng tính chất góc giữa hai đường thẳng sẽ bằng góc giữa hai vectơ chỉ phương của chúng.
Lời giải chi tiết:
Vectơ pháp tuyến của mặt phẳng \((\alpha )\) là \(\vec n\), và của mặt phẳng \((\beta )\) là \(\vec n'\).
Nếu hai đường thẳng \(a\) và \(a'\) vuông góc với \((\alpha )\), và \(b\) và \(b'\) vuông góc với \((\beta )\), thì hai vectơ \(\vec n\) và \(\vec n'\)lần lượt là hai vectơ chỉ phương của \(a\) và \(a'\), \(b\) và \(b'\).
Mà góc giữa hai đường thẳng bằng góc giữa hai vectơ chỉ phương của chúng nên
\((a,b) = (a',b')\) do cùng bằng với góc \((\overrightarrow n ,\overrightarrow {n'} )\).
Vậy nếu \(\vec a\) vuông góc với \((\alpha )\) và \(\vec b\) vuông góc với \((\beta )\), thì hai góc \((a,b)\) và \((a',b')\) sẽ bằng nhau vì cùng liên quan đến vectơ pháp tuyến \(\vec n\) và \(\vec n'\).
LT3
Trả lời câu hỏi Luyện tập 3 trang 70 SGK Toán 12 Cùng khám phá
Trong không gian Oxyz, tính góc giữa mặt phẳng \((\alpha ):\sqrt 3 x - y + 2 = 0\) và các mặt phẳng toạ độ \((Oxy)\), \((Oxz)\), \((Oyz)\).
Phương pháp giải:
- Xác định vectơ pháp tuyến của mặt phẳng \((\alpha )\).
- Góc giữa hai mặt phẳng là góc giữa các vectơ pháp tuyến của chúng:
\(\cos \theta = \frac{{{{\vec n}_1} \cdot {{\vec n}_2}}}{{|{{\vec n}_1}||{{\vec n}_2}|}}\)
Trong đó, \({\vec n_1} \cdot {\vec n_2}\) là tích vô hướng, \(|{\vec n_1}|\) và \(|{\vec n_2}|\) là độ lớn của các vectơ.
Lời giải chi tiết:
Cho mặt phẳng \((\alpha )\): \(\sqrt 3 x - y + 2 = 0\).
Vectơ pháp tuyến của mặt phẳng \(\alpha \): \({\vec n_\alpha } = (\sqrt 3 , - 1,0)\).
Góc giữa mặt phẳng \((\alpha )\) và Oxy:
- Vectơ pháp tuyến của Oxy: \({\vec n_{Oxy}} = (0,0,1)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxy}} = \sqrt 3 .0 + ( - 1).0 + 0.1 = 0\)
Độ lớn:
\(|{\vec n_\alpha }| = \sqrt {3 + 1 + 0} = 2,\quad |{\vec n_{Oxy}}| = \sqrt {0 + 0 + 1} = 1\)
\(\cos \theta = \frac{0}{{2 \times 1}} = 0\quad \Rightarrow \theta = {90^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oxz:
- Vectơ pháp tuyến của Oxz: \({\vec n_{Oxz}} = (0,1,0)\).
Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oxz}} = \sqrt 3 .0 + ( - 1).1 + 0.0 = - 1\)
Độ lớn:
\(|{\vec n_{Oxz}}| = \sqrt {0 + 1 + 0} = 1\)
\(\cos \theta = \frac{{ - 1}}{{2 \times 1}} = - \frac{1}{2}\quad \Rightarrow \theta = {120^\circ }\)
Góc giữa mặt phẳng \((\alpha )\) và Oyz:
- Vectơ pháp tuyến của Oyz: \({\vec n_{Oyz}} = (1,0,0)\). Tích vô hướng:
\({\vec n_\alpha } \cdot {\vec n_{Oyz}} = \sqrt 3 .1 + ( - 1).0 + 0.0 = \sqrt 3 \)
Độ lớn:
\(|{\vec n_{Oyz}}| = \sqrt {1 + 0 + 0} = 1\)
\(\cos \theta = \frac{{\sqrt 3 }}{{2 \times 1}} = \frac{{\sqrt 3 }}{2}\quad \Rightarrow \theta = {30^\circ }\)
VD
Trả lời câu hỏi Vận dụng trang 70 SGK Toán 12 Cùng khám phá
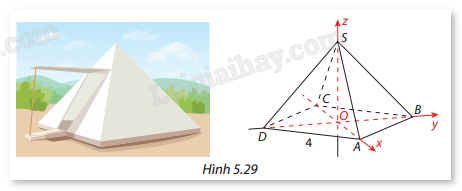
Để chuẩn bị cho chuyến đi dã ngoại, nhóm bạn Đức thiết kế lều cắm trại dạng hình chóp từ giác đều có đáy là hình vuông cạnh 4m. Theo bản vẽ thiết kế thì góc giữa hai mặt bên của lều bằng 60°. Bằng phương pháp tọa độ, hãy tính chiều cao của lều này.
Phương pháp giải:
- Xây dựng hệ tọa độ và xác định tọa độ các điểm
- Xác định vector pháp tuyến của các mặt bên
- Sử dụng công thức tính góc giữa hai mặt phẳng qua vector pháp tuyến
- Giải phương trình để tìm chiều cao
Lời giải chi tiết:
Gọi h là chiều cao cần tìm của hình chóp S.ABCD.
Do mặt đáy là hình vuông cạnh 4m nên \(OA = OB = OC = OD = 2\sqrt 2 \)
Toạ độ các điểm là \(A(2\sqrt 2 ;0;0)\), \(B(0;2\sqrt 2 ;0)\), \(C( - 2\sqrt 2 ;0;0)\), \(D(0; - 2\sqrt 2 ;0)\) và \(S(0;0;h)\).
Vectơ chỉ phương của mặt phẳng SAB là \(\overrightarrow {AB} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SA} = (2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SAB là
\(\overrightarrow {{n_{SAB}}} = \overrightarrow {AB} .\overrightarrow {SA} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.2\sqrt 2 - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .2\sqrt 2 = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h; - 8)\)
Vectơ chỉ phương của mặt phẳng SCD là \(\overrightarrow {DC} = ( - 2\sqrt 2 ;2\sqrt 2 ;0)\) và \(\overrightarrow {SC} = ( - 2\sqrt 2 ;0; - h)\)
Suy ra vectơ pháp tuyến của mặt phẳng SCD là
\(\overrightarrow {{n_{SCD}}} = \overrightarrow {DC} .\overrightarrow {SC} = (2\sqrt 2 .( - h) - 0.0;\,\,\,0.( - 2\sqrt 2 ) - ( - 2\sqrt 2 ).( - h);\,\,\,( - 2\sqrt 2 ).0 - 2\sqrt 2 .( - 2\sqrt 2 )) = ( - 2\sqrt 2 .h; - 2\sqrt 2 .h;8)\)
Ta có:
\(\overrightarrow {{n_{SAB}}} .\overrightarrow {{n_{SCD}}} = 8{h^2} + 8{h^2} - 64 = 16{h^2} - 64 = 16({h^2} - 4)\)
\(\left| {\overrightarrow {{n_{SAB}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
\(\left| {\overrightarrow {{n_{SCD}}} } \right| = \sqrt {8{h^2} + 8{h^2} + 64} = \sqrt {16{h^2} + 64} = 4\sqrt {{h^2} + 4} \)
Góc giữa hai mặt phẳng SAB và SCD bằng 60° nên suy ra:
\(\cos 60^\circ = \frac{{16({h^2} - 4)}}{{4\sqrt {{h^2} + 4} .4\sqrt {{h^2} + 4} }} = \frac{{16({h^2} - 4)}}{{16({h^2} + 4)}} = \frac{{{h^2} - 4}}{{{h^2} + 4}} = \frac{1}{2}\)
\( \Leftrightarrow 2{h^2} - 8 = {h^2} + 4\)
\( \Leftrightarrow {h^2} = 12\)
\( \Leftrightarrow h = \sqrt {12} = 2\sqrt 3 \)
Vậy chiều cao của lều là \(2\sqrt 3 \)m.
- Giải bài tập 5.24 trang 70 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.25 trang 70 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.26 trang 71 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.27 trang 71 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 5.28 trang 71 SGK Toán 12 tập 2 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá













Danh sách bình luận