Lý thuyết Góc nội tiếp Toán 9 Kết nối tri thức

Định nghĩa góc nội tiếp Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong góc được gọi là cung bị chắn.

Định nghĩa góc nội tiếp

Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Cung nằm bên trong góc được gọi là cung bị chắn.

Ví dụ:

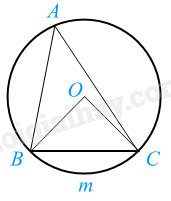
- Góc BAC là góc nội tiếp của đường tròn (O);

- Góc nội tiếp BAC chắn cung $\overset\frown{BmC}$.

Định lí mối liên hệ giữa góc nội tiếp với cung bị chắn

Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

Ví dụ:

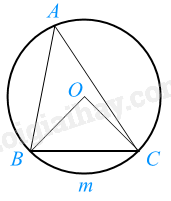
$\widehat {BAC} = \frac{1}{2}$sđ$\overset\frown{BmC}=\frac{1}{2}\widehat{BOC}$.

Nhận xét: Đối với góc nội tiếp của cùng một đường tròn hoặc của hai đường tròn bằng nhau, ta có các khẳng định sau:

+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

+ Các góc nội tiếp chắn cung nhỏ thì có số đo bằng nửa số đo của góc ở tâm chắn cùng một cung.

+ Góc nội tiếp chắn nửa đường tròn là góc vuông.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải câu hỏi trang 68, 69, 70 SGK Toán 9 tập 2 - Kết nối tri thức
Vẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2). a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB. b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh. c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB.
Giải bài tập 9.1 trang 70 SGK Toán 9 tập 2 - Kết nối tri thức
Những khẳng định nào sau đây là đúng? a) Hai góc nội tiếp bằng nhau thì cùng chắn một cung. b) Góc nội tiếp nhỏ hơn ({90^o}) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung. c) Góc nội tiếp chắn cung nhỏ có số đo bằng số đo của góc ở tâm cùng chắn một cung. d) Hai góc nội tiếp bằng nhau thì chắn hai cung bằng nhau.
Giải bài tập 9.2 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức
Cho các điểm như Hình 9.7. Tính số đo các góc của tam giác ABC, biết rằng (widehat {AOB} = {120^o},widehat {BOC} = {80^o}).
Giải bài tập 9.3 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức
Cho đường tròn (O) và hai dây cung AC, BD cắt nhau tại X (H.9.8). Tính số đo góc AXB biết rằng (widehat {ADB} = {30^o},widehat {DBC} = {50^o}).
Giải bài tập 9.4 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại điểm I nằm trong (O) (H.9.9). a) Biết rằng (widehat {AOC} = {60^o},widehat {BOD} = {80^o}). Tính số đo của góc AID. b) Chứng minh rằng (IA.IB = IC.ID).
Giải bài tập 9.5 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức
Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A), N (khác B). Gọi P là giao điểm của BM và AN (H.9.10). Chứng minh rằng SP vuông góc với AB.
Giải bài tập 9.6 trang 71 SGK Toán 9 tập 2 - Kết nối tri thức
Trên sân bóng, khi trái bóng được đặt tại điểm phạt đền thì có góc sút bằng ({36^o}) và trái bóng cách mỗi cọc gôn 11,6m (H.9.11). Hỏi khi trái bóng đặt ở vị trí cách điểm phạt đền 11,6m thì góc sút bằng bao nhiêu?