Lý thuyết Căn bậc ba Toán 9 Chân trời sáng tạo

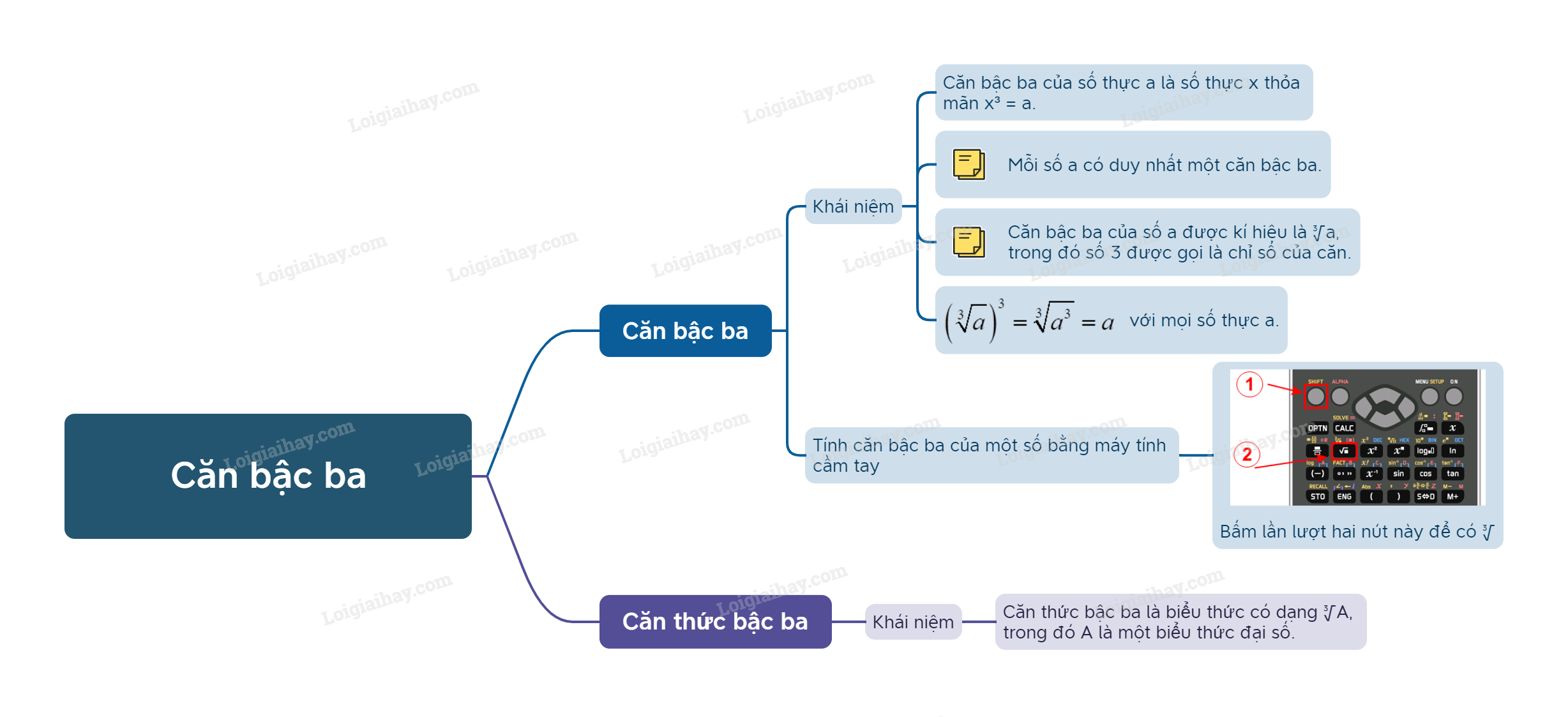
1. Căn bậc ba của một số Khái niệm căn bậc ba của một số thực

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

1. Căn bậc ba của một số

Khái niệm căn bậc ba của một số thực

- Cho số thực a. Số thực x thỏa mãn \({x^3} = a\) được gọi là căn bậc ba của a.

- Mỗi số thực a đều có đúng một căn bậc ba, kí hiệu là \(\sqrt[3]{a}\).

Trong kí hiệu \(\sqrt[3]{a}\), số 3 được gọi là chỉ số căn. Phép toán tìm căn bậc ba của một số gọi là phép khai căn bậc hai.

Chú ý: Từ định nghĩa căn bậc ba, ta có \({\left( {\sqrt[3]{a}} \right)^3} = \sqrt[3]{{{a^3}}} = a\).

Ví dụ:

\(\sqrt[3]{{64}} = \sqrt[3]{{{4^3}}} = 4\);

\(\sqrt[3]{{ - 27}} = \sqrt[3]{{{{\left( { - 3} \right)}^3}}} = - 3\).

2. Tính căn bậc ba của một số bằng máy tính cầm tay

Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.

Ví dụ:

3. Căn thức bậc ba

Khái niệm

Với A là một biểu thức đại số, ta gọi \(\sqrt[3]{A}\) là căn thức bậc ba của A.

Ví dụ: Với \(x = 60\), giá trị của \(\sqrt[3]{{2x + 5}}\) là:

\(\sqrt[3]{{2.60 + 5}} = \sqrt[3]{{125}} = \sqrt[3]{{{5^3}}} = 5\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 42, 43 SGK Toán 9 tập 1 - Chân trời sáng tạo
Có hai khối bê tông hình lập phương A và B có thể tích lần lượt là 8 dm3 và 15 dm3 (Hình 1). a) Tính độ dài cạnh của khối bê tông A. b) Gọi x (dm) là độ dài cạnh của khối bê tông B. Thay ? bằng số thích hợp để có đẳng thức: x3 = ?
Giải mục 2 trang 44 SGK Toán 9 tập 1 - Chân trời sáng tạo
Sử dụng máy tính cầm tay, tìm căn bậc ba của các số sau (kết quả làm tròn dến chữ số thập phân thứ ba): a) 25 b) -100 c) 8,5 d) (frac{1}{5})
Giải mục 3 trang 44 SGK Toán 9 tập 1 - Chân trời sáng tạo
Ông An có một bể kính hình lập phương như Hình 2. Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính). a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức: a3 = ? hay a = ?. b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai).
Giải bài tập 1 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tìm căn bậc ba của mỗi số sau: a) -64 b) 27000 c) – 0,125 d) (3frac{3}{8})
Giải bài tập 2 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tính a) (sqrt[3]{{0,001}}) b) (sqrt[3]{{ - frac{1}{{64}}}}) c) ( - sqrt[3]{{{{11}^3}}}) d) ({left( {sqrt[3]{{ - 216}}} right)^3})
Giải bài tập 3 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo
Hoàn thành bảng sau vào vở:
Giải bài tập 4 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo
Sử dụng máy tính cầm tay, tính (kết quả làm tròn đến chữ số thập phân thứ ba): a) (sqrt[3]{{79}}) b) (sqrt[3]{{ - 6,32}}) c) (frac{{sqrt[3]{{19}} + sqrt[3]{{20}}}}{2})
Giải bài tập 5 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tính giá trị của các biểu thức: a) A = (sqrt[3]{{{8^3}}} + {left( {sqrt[3]{{ - 7}}} right)^3}) b) B = (sqrt[3]{{1000000}} - sqrt[3]{{0,027}})
Giải bài tập 6 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tìm x, biết: a) x3 = - 27 b) x3 = (frac{{64}}{{125}}) c) (sqrt[3]{x} = 8) d) (sqrt[3]{x} = - 0,9)
Giải bài tập 7 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo
Tính giá trị của biểu thức P = (sqrt[3]{{64n}}) khi n = 1; n = - 1; n = (frac{1}{{125}}).
Giải bài tập 8 trang 45 SGK Toán 9 tập 1 - Chân trời sáng tạo
Một khối hình lập phương có thể tích 1000 cm3 . Chia khối gỗ này thành 8 khối gỗ hình lập phương nhỏ có thể tích bằng nhau. Tính độ dài cạnh của mỗi khối gỗ hình lập phương nhỏ.