 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài 2. Công thức xác suất toàn phần và công thức Bayes ..
Bài 2. Công thức xác suất toàn phần và công thức Bayes ..
Giải mục 2 trang 77, 78, 79 SGK Toán 12 tập 2 - Chân trời sáng tạo
Khảo sát thị lực của 100 học sinh, ta thu được bảng số liệu sau: Chọn ngẫu nhiên 1 bạn trong 100 học sinh trên. a) Biết rằng bạn đó có tật khúc xạ, tính xác suất bạn đó là học sinh nam. b) Biết rằng bạn đó là học sinh nam, tính xác suất bạn đó có tật khúc xạ.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 77 SGK Toán 12 Chân trời sáng tạo
Khảo sát thị lực của 100 học sinh, ta thu được bảng số liệu sau:
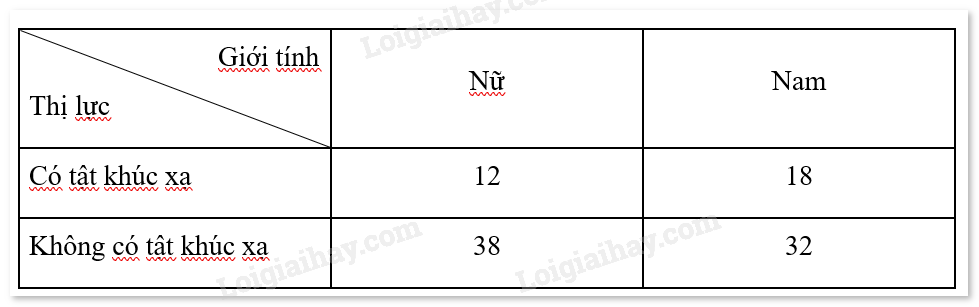
Chọn ngẫu nhiên 1 bạn trong 100 học sinh trên.
a) Biết rằng bạn đó có tật khúc xạ, tính xác suất bạn đó là học sinh nam.
b) Biết rằng bạn đó là học sinh nam, tính xác suất bạn đó có tật khúc xạ.
Phương pháp giải:
a) Tính số bạn bị tật khúc xạ, sau đó tính xác suất chọn được 1 bạn nam trong số những bạn bị tật khúc xạ.
b) Tính tổng số bạn nam, sau đó tính xác suất chọn được 1 bạn bị tật khúc xạ trong số những bạn nam.
Lời giải chi tiết:
a) Có tất cả \(12 + 18 = 30\) bạn bị tật khúc xạ, trong đó có 18 bạn nam. Vậy xác suất của biến cố là \(\frac{{18}}{{30}} = 0,6\).
b) Có tất cả \(18 + 32 = 50\) bạn nam, trong đó có 18 bạn bị tật khúc xạ. Vậy xác suất của biến cố là \(\frac{{18}}{{50}} = 0,36\).
TH2
Trả lời câu hỏi Thực hành 2 trang 79 SGK Toán 12 Chân trời sáng tạo
Khi phát hiện một vật thể bay, xác suất một hệ thống radar phát cảnh báo là 0,9 nếu vật thể bay đó là mục tiêu thật và là 0,05 nếu đó là mục tiêu giả. Có 99% các vật thể bay là mục tiêu giả. Biết rằng hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay. Tính xác suất vật thể đó là mục tiêu thật.

Phương pháp giải:
Gọi \(A\) là biến cố “Radar phát cảnh báo”, \(B\) là biến cố “Vật thể bay là mục tiêu thật”.
Xác suất cần tính là \(P\left( {B|A} \right)\). Theo đề bài, xác định \(P\left( A \right)\), \(P\left( B \right)\) và \(P\left( {A|B} \right)\), rồi sử dụng công thức Bayes.
Lời giải chi tiết:
Gọi \(A\) là biến cố “Radar phát cảnh báo”, \(B\) là biến cố “Vật thể bay là mục tiêu thật”.
Xác suất cần tính là \(P\left( {B|A} \right)\).
Theo đề bài, ta có \(P\left( {A|B} \right) = 0,9\); \(P\left( {A|\bar B} \right) = 0,05\); \(P\left( B \right) = 1 - 0,99 = 0,01\) và \(P\left( {\bar B} \right) = 0,99\).
Áp dụng công thức tính xác suất toàn phần, ta có:
\(P\left( A \right) = P\left( B \right)P\left( {A|B} \right) + P\left( {\bar B} \right)P\left( {A|\bar B} \right) \)
\(= 0,01.0,9 + 0,99.0,05 = 0,0585\).
Vậy khi radar phát cảnh báo, xác suất vật thể đó là mục tiêu thật là:
\(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}} = \frac{{0,01.0,9}}{{0,0585}} = \frac{2}{{13}}\).
VD
Trả lời câu hỏi Vận dụng trang 79 SGK Toán 12 Chân trời sáng tạo
Người ta điều tra thấy ở một địa phương nọ có 2% tài xế sử dụng điện thoại di động khi lái xe. Trong các vụ tai nạn ở địa phương đó, người ta nhận thấy có 10% là do tài xế có sử dụng điện thoại khi lái xe gây ra. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?
Phương pháp giải:
Gọi \(A\) là biến cố “Tài xế gây tai nạn”, \(B\) là biến cố “Tài xế có sử dụng điện thoại di động”. Ta cần so sánh \(P\left( {A|B} \right)\) và \(P\left( {A|\bar B} \right)\). Sử dụng công thức xác suất toàn phần và công thức Bayes, từ đó kết luận.
Lời giải chi tiết:
Gọi \(A\) là biến cố “Tài xế gây tai nạn”, \(B\) là biến cố “Tài xế có sử dụng điện thoại di động”. Suy ra \(P\left( {A|B} \right)\) là xác suất tài xế gây tai nạn khi sử dụng điện thoại, và \(P\left( {A|\bar B} \right)\) là xác suất tài xế gây tai nạn khi không sử dụng điện thoại.
Theo đề bài ta có \(P\left( B \right) = 0,02\), \(P\left( {B|A} \right) = 0,1\), suy ra \(P\left( {\bar B} \right) = 1 - 0,02 = 0,98\) và \(P\left( {\bar B|A} \right) = 1 - 0,1 = 0,9\).
Áp dụng công thức xác suất toàn phần, ta có
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\bar B} \right).P\left( {A|\bar B} \right)\)
\(= 0,02.P\left( {A|B} \right) + 0,98.P\left( {A|\bar B} \right)\).
Mặt khác, theo công thức Bayes: \(P\left( {B|A} \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( A \right)}} \)
\(\Rightarrow P\left( A \right) = \frac{{P\left( B \right).P\left( {A|B} \right)}}{{P\left( {B|A} \right)}} = \frac{{0,02.P\left( {A|B} \right)}}{{0,1}} = 0,2.P\left( {A|B} \right)\)
Suy ra \(0,2.P\left( {A|B} \right) = 0,02.P\left( {A|B} \right) + 0,98P\left( {A|\bar B} \right) \)
\(\Rightarrow 0,18.P\left( {A|B} \right) = 0,98.P\left( {A|\bar B} \right)\).
Vậy \(\frac{{P\left( {A|B} \right)}}{{P\left( {A|\bar B} \right)}} = \frac{{0,98}}{{0,18}} = \frac{{49}}{9} \approx 5,4\). Điều đó có nghĩa khi sử dụng điện thoại, xác suất tài xế gây tai nạn khi lái xe sẽ tăng khoảng 5,4 lần.
- Giải bài tập 1 trang 79 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 2 trang 79 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 3 trang 79 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 4 trang 79 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải mục 1 trang 76, 77 SGK Toán 12 tập 2 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận