Giải bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo

Xét một chất điểm chuyển động dọc theo trục (Ox). Toạ độ của chất điểm tại thời điểm (t) được xác định bởi hàm số (x(t) = {t^3} - 6{t^2} + 9t) với (t ge 0). Khi đó (x'(t)) là vận tốc của chất điểm tại thời điểm (t), kí hiệu (v(t)); (v'(t)) là gia tốc chuyển động của chất điểm tại thời điểm (t), kí hiệu (a(t)). a) Tìm các hàm (v(t))và (a(t)) b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Xét một chất điểm chuyển động dọc theo trục \(Ox\). Toạ độ của chất điểm tại thời điểm \(t\) được xác định bởi hàm số \(x(t) = {t^3} - 6{t^2} + 9t\) với \(t \ge 0\). Khi đó \(x'(t)\) là vận tốc của chất điểm tại thời điểm \(t\), kí hiệu \(v(t)\); \(v'(t)\) là gia tốc chuyển động của chất điểm tại thời điểm \(t\), kí hiệu \(a(t)\).
a) Tìm các hàm \(v(t)\)và \(a(t)\)
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?

Phương pháp giải - Xem chi tiết

Áp dụng công thức tính đạo hàm, xét dấu đạo hàm.

Lời giải chi tiết

a) \(v(t) = x'(t) = 3{t^2} - 12t + 9\).

\(a(t) = v'(t) = 6t - 12\).

b) Tập xác định: \(D = [0; + \infty )\).

\(a(t) = 0 \Leftrightarrow t = 2\).

Vận tốc chất điểm tăng nghĩa là đồ thị hàm v(t) đi lên từ trái sang, vận tốc chất điểm giảm nghĩa là đồ thị hàm v(x) đi xuống từ trái sang.

Để xét sự biến thiên đồ thị hàm v(t), ta xét dấu v'(t) = a(t).

Bảng biến thiên:

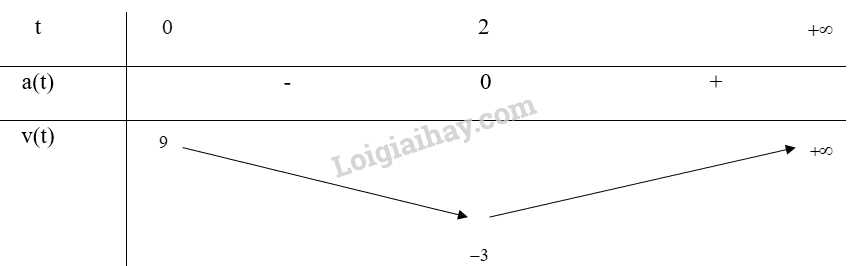
Vậy trong khoảng từ t = 0 đến t = 2 thì vận tốc của chất điểm giảm, từ t = 2 trở đi thì vận tốc của chất điểm tăng.

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài tiếp theo

Giải bài tập 7 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Đạo hàm f '(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).
Giải bài tập 5 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức (fleft( x right) = 0,01{x^3}--0,04{x^2} + 0,25x + 0,44) (tỉ USD) với x là số năm tính từ 2010 đến 2017 ((0 le x le 7)). a) Tính đạo hàm của hàm số y = f(x). b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Giải bài tập 4 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chứng minh rằng hàm số (y = frac{{2x + 1}}{{x - 3}}) nghịch biến trên từng khoảng xác định của nó
Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm cực trị của các hàm số sau: a) (y = 2{x^3} + 3{x^2}--36x + 1) b) (y = frac{{{x^2} - 8x + 10}}{{x - 2}}) c) (y = sqrt { - {x^2} + 4} )
Giải bài tập 2 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau: a) (y = 4{x^3} + 3{x^2}--36x + 6) b) (y = frac{{{x^2} - 2x - 7}}{{x - 4}})
Giải bài tập 1 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
Giải mục 2 trang 10, 11, 12 SGK Toán 12 tập 1 - Chân trời sáng tạo
Cực trị của hàm số
Giải mục 1 trang 6, 7, 8 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tính đơn điệu của hàm số
Giải câu hỏi mở đầu trang 6 SGK Toán 12 tập 1 - Chân trời sáng tạo
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\). Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?
Lý thuyết Tính đơn điệu và cực trị của hàm số Toán 12 Chân trời sáng tạo
Bài 1. Tính đơn điệu và cực trị của hàm số 1. Tính đơn điệu của hàm số