Giải bài tập 5.6 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức

Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm. a) Tính khoảng cách từ O đến đường thẳng AB. b) Tính(tan alpha )nếu góc ở tâm chắn cung AB bằng (2alpha .)

Đề bài

Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

a) Tính khoảng cách từ O đến đường thẳng AB.

b) Tính\(\tan \alpha \)nếu góc ở tâm chắn cung AB bằng \(2\alpha .\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Gọi H là trung điểm của AB, chứng minh \(OH \bot AB\) hay khoảng cách từ O đến đường thẳng AB bằng độ dài đoạn OH. Sau đó áp dụng định lý Pythagore để tính OH.

b) \(\widehat {AOB} = 2\alpha\) suy ra \( \alpha = \widehat {HOA}\). Xét tam giác OAH để tính \(\tan \alpha .\)

Lời giải chi tiết

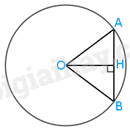
a) Kẻ \( OH \bot AB\).

Ta có \(\Delta AOB\) cân tại O (OA = OB), OH là đường cao nên OH cũng là đường trung tuyên của \(\Delta OAB\)

Suy ra H là trung điểm của AB nên \(AH = HB = 3cm\)

Xét \(\Delta AHO\) vuông tại H, áp dụng định lý Pythagore, ta có:

\(OH = \sqrt{OA^2-AH^2} = \sqrt{5^2-3^2}= 4 (cm)\)

Vậy khoảng cách từ O đến AB là 4cm.

b) Ta có: \(\widehat{AOB} = 2\alpha \).

OH là đường cao của tam giác AOB cân tại O nên OH cũng là đường phân giác của \(\widehat{AOB}\)

Suy ra \(\widehat {AOH} = \widehat{BOH} = \alpha\)

Tam giác AOH vuông tại H nên ta có:

\(tan\alpha = \frac{AH}{OH} = \frac{3}{4}\)

Bình luận

Chia sẻ

Bình chọn:

4 trên 8 phiếu

Bài tiếp theo

Giải bài tập 5.7 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức
Tâm O của một đường tròn cách dây AB của nó một khoảng 3 cm. Tính bán kính của đường tròn (O), biết rằng dây cung nhỏ AB có số đo bằng (100^circ )(làm tròn kết quả đến hàng phần mười).
Giải bài tập 5.8 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức
Trên mặt một chiếc đồng hồ có các vạch chia như Hình 5.12. Hỏi cứ sau mỗi khoảng thời gian 36 phút: a) Đầu kim phút vạch trên một cung có số đo bằng bao nhiêu độ? b) Đầu kim giờ vạch trên một cung có số đo bằng bao nhiêu độ?
Giải bài tập 5.5 trang 90 SGK Toán 9 tập 1 - Kết nối tri thức
Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn (frac{{AB}}{2}.)
Giải mục 2 trang 89, 90 SGK Toán 9 tập 1 - Kết nối tri thức
Tại sao số đo cung lớn của một đường tròn luôn lớn hơn ({180^0})
Giải mục 1 trang 87, 88 SGK Toán 9 tập 1 - Kết nối tri thức
Xét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R.
Lý thuyết Cung và dây của một đường tròn Toán 9 Kết nối tri thức
1. Dây và đường kính của đường tròn Khái niệm dây