Giải bài tập 4 trang 91 SGK Toán 9 tập 1 - Cánh diều

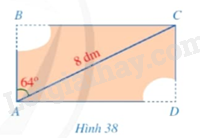
Một mảnh gỗ có dạng hình chữ nhật (ABCD) với đường chéo (AC = 8dm). Do bảo quản không tốt nên mảnh gỗ bị hỏng phía hai đỉnh (B) và (D). Biết (widehat {BAD} = 64^circ ) (Hình 38). Người ta cần biết độ dài (AB) và (AD) để khôi phục mảnh gỗ ban đầu. Độ dài (AB,AD) bằng bao nhiêu decimét (làm tròn kết quả đến hàng phần mười)?

Đề bài

Một mảnh gỗ có dạng hình chữ nhật \(ABCD\) với đường chéo \(AC = 8dm\). Do bảo quản không tốt nên mảnh gỗ bị hỏng phía hai đỉnh \(B\) và \(D\). Biết \(\widehat {BAD} = 64^\circ \) (Hình 38). Người ta cần biết độ dài \(AB\) và \(AD\) để khôi phục mảnh gỗ ban đầu. Độ dài \(AB,AD\) bằng bao nhiêu decimét (làm tròn kết quả đến hàng phần mười)?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải chi tiết

Do \(ABCD\) là hình chữ nhật nên \(AD = BC\).

Xét tam giác \(ABC\) vuông tại \(B\) ta có:

+ \(BC = AC.\sin 64^\circ = 8.\sin 64^\circ \approx 7,2\left( {dm} \right)\) nên \(AD \approx 7,2\left( {dm} \right)\).

+ \(AB = AC.\cos 64^\circ = 8.\cos 64^\circ \approx 3,5\left( m \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 5 phiếu

Bài tiếp theo

Giải bài tập 5 trang 91 SGK Toán 9 tập 1 - Cánh diều
Trên mặt biển, khi khoảng cách (AB) từ ca nô đến chân tháp hải đăng là 250m, một người đứng trên tháp hải đăng đó nhìn về phía ca nô theo phương (CA) tạo với phương nằm ngang (Cx) một góc là (widehat {ACx} = 32^circ ) (Hình 39). Tính chiều cao của tháp hải đăng (làm tròn kết quả đến hàng phần mười của mét), biết (AB//Cx) và độ cao từ tầm mắt của người đó đến đỉnh tháp là 3,2m.
Giải bài tập 3 trang 91 SGK Toán 9 tập 1 - Cánh diều
Trong công việc, người ta cần ước lượng khoảng cách từ vị trí (O) đến khu đất có dạng hình thang (MNPQ) nhưng không thể đo được trực tiếp, khoảng cách đó được tính bằng khoảng cách từ (O) đến đường thẳng (MN). Người ta chọn vị trí (A) ở đáy (MN) và đo được (OA = 18m,widehat {OAN} = 44^circ ) (Hình 37). Tính khoảng cách từ vị trí (O) đến khu đất (làm tròn kết quả đến hàng phần mười của mét).
Giải bài tập 2 trang 91 SGK Toán 9 tập 1 - Cánh diều
Để ước lượng chiều cao của một cây trong sân trường, bạn Hoàng đứng ở sân trường (theo phương thẳng đứng), mặt bạn Hoàng đặt tại vị trí (C) cách mặt đất một khoảng (CB = DH = 1,64m) và cách cây một khoảng (CD = BH = 6m). Tính chiều cao (AH) của cây (làm tròn kết quả đến hàng phần trăm của mét), biết góc nhìn (ACD) bằng (38^circ ) minh họa ở Hình 36.
Giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều
Hình 35 mô tả ba vị trí (A,B,C) là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ (C) đến (A) và từ (C) đến (B). Biết (AB = 50m), (widehat {ABC} = 40^circ ). Tính khoảng cách (CA) và (CB) (làm tròn kết quả đến hàng đơn vị của mét).
Giải mục 2 trang 90 SGK Toán 9 tập 1 - Cánh diều
Mặt cắt đứng của khung thép có dạng tam giác cân (ABC) với (widehat B = 23^circ ,AB = 4m) (Hình 33). Tính độ dài đoạn thẳng (BC) (làm tròn kết quả đến hàng phần mười của mét).
Giải mục 1 trang 89 SGK Toán 9 tập 1 - Cánh diều
Hãy giải bài toán ở phần mở đầu và tính (AB) trong Hình 29b (làm tròn kết quả đến hàng phần trăm của mét).
Giải câu hỏi khởi động trang 88 SGK Toán 9 tập 1 - Cánh diều
Hình 28 minh hoạ một máy bay cất cánh từ vị trí (A) trên đường băng của sân bay và bay theo đường thẳng (AB) tạo với phương nằm ngang (AC) một góc là (20^circ ). Sau 5 giây, máy bay ở độ cao (BC = 110m). Có thể tính khoảng cách (AB) bằng cách nào?