 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài 2. Toạ độ của vectơ trong không gian - Toán 12 Chân..
Bài 2. Toạ độ của vectơ trong không gian - Toán 12 Chân..
Giải bài tập 3 trang 56 SGK Toán 12 tập 1 - Chân trời sáng tạo
Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2 (Hình 13). a) Xác định một hệ toạ độ dựa trên gợi ý của hình vẽ và chỉ ra các vectơ đơn vị trên các trục toạ độ. b) Tìm toạ độ các điểm A, B, C, S.
Đề bài
Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2 (Hình 13).
a) Xác định một hệ toạ độ dựa trên gợi ý của hình vẽ và chỉ ra các vectơ đơn vị trên các trục toạ độ.
b) Tìm toạ độ các điểm A, B, C, S.

Phương pháp giải - Xem chi tiết
Quan sát hình vẽ.
Lời giải chi tiết
a)
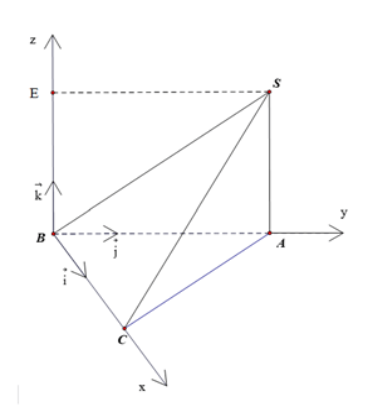
b) \(\overrightarrow {BA} = 2\overrightarrow j \Rightarrow A(0;2;0)\).
B trùng với gốc tọa độ O nên B(0;0;0).
\(\overrightarrow {BC} = 3\overrightarrow i \Rightarrow C(3;0;0)\).
Gọi E là hình chiếu của S lên Oz. Theo quy tắc hình bình hành ta có:
\(\overrightarrow {BS} = 2\overrightarrow j + 2\overrightarrow k \Rightarrow S(0;2;2)\).
- Giải bài tập 4 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 5 trang 58 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 7 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Giải bài tập 2 trang 56 SGK Toán 12 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận